Teoría de números para niños
La teoría de números es una parte de las matemáticas que se dedica a estudiar las propiedades de los números, especialmente los números enteros. También analiza los problemas que surgen al trabajar con ellos.
Un matemático famoso, Jürgen Neukirch, dijo una vez que la teoría de números es tan importante en las matemáticas como las matemáticas lo son para otras ciencias.
Los números enteros se pueden estudiar por sí mismos o como soluciones de ecuaciones. A veces, para entender mejor la teoría de números, se usan herramientas de otras áreas de las matemáticas, como el análisis complejo. También se pueden estudiar los números reales en relación con los números racionales, por ejemplo, para ver cómo se aproximan unos a otros.
Antiguamente, a la teoría de números se le llamaba "aritmética". A veces se le decía "alta aritmética", pero esos términos ya no se usan mucho. Es importante no confundir esto con la aritmética básica que aprendemos en la escuela, o con la parte de la lógica que estudia los axiomas de Peano. Los matemáticos que estudian la teoría de números se llaman teóricos de números.
Contenido
Historia de la Teoría de Números
Los primeros pasos
El inicio de la aritmética
El registro más antiguo que tenemos sobre aritmética es un pedazo de una tabla de arcilla llamada Plimpton 322. Fue encontrada en Larsa, Mesopotamia, y data de hace unos 3800 años (alrededor del 1800 a.C.). Esta tablilla contiene una lista de "triples pitagóricos". Estos son grupos de tres números enteros (a, b, c) que cumplen la regla de que a² + b² = c².
Los números en la tabla son muy grandes y hay muchos, lo que sugiere que no fueron encontrados al azar. La forma en que está organizada la tabla indica que se usó una fórmula para crearlos. No se sabe para qué se usaban exactamente, pero algunos creen que eran ejemplos para problemas escolares.
En Babilonia, las matemáticas, especialmente el álgebra, estaban muy avanzadas. Se dice que Pitágoras aprendió matemáticas de los babilonios. También se cuenta que Tales y Pitágoras viajaron y estudiaron en Egipto.
En los libros de Euclides, especialmente del IX 21 al 34, se encuentran ideas que probablemente vienen de los pitagóricos. Son ideas sencillas, como "un número impar multiplicado por un número par da un número par". Estas ideas son importantes para demostrar que la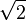 
es un número irracional.
Los pitagóricos le daban mucha importancia a los números pares e impares. El descubrimiento de que 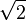es irracional se atribuye a ellos. Este hallazgo causó una gran sorpresa en las matemáticas de la época. Hizo que se distinguiera entre los números (enteros y racionales) y las longitudes o proporciones (lo que hoy llamamos números reales).
La tradición pitagórica también hablaba de los números poligonales o números figurados. Estos son números que se pueden representar con formas geométricas, como triángulos o pentágonos.
No hay mucha información sobre aritmética en los textos egipcios antiguos o védicos. Sin embargo, el teorema del resto chino aparece en un libro llamado Sunzi Suanjing (entre los siglos III y V d.C.).
La Grecia clásica y el período helenístico temprano
Las matemáticas de la Grecia clásica se conocen por escritos de la época o por obras matemáticas helenísticas. En la teoría de números, esto significa principalmente las ideas de Platón y Euclides.
Aunque las matemáticas de Asia influyeron en Grecia, las matemáticas griegas también tienen su propia tradición. Eusebio de Cesarea menciona que Pitágoras viajó y aprendió de muchas culturas, pero que los sabios de Grecia no le enseñaron nada nuevo.
Platón estaba muy interesado en las matemáticas. Él diferenciaba entre aritmética (el estudio de los números) y cálculo. Gracias a uno de sus diálogos, el Teteto, sabemos que Teodoro demostró que raíces como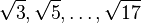 
son irracionales. Teteto, un alumno de Teodoro, trabajó en clasificar los diferentes tipos de números incomensurables.
Euclides dedicó parte de sus Elementos a los números primos y la divisibilidad. Estos son temas fundamentales en la teoría de números. Por ejemplo, dio un método para encontrar el máximo común divisor de dos números (el algoritmo de Euclides) y la primera prueba conocida de que hay infinitos números primos.
En 1773, Lessing encontró un problema matemático en un manuscrito, conocido como el problema del ganado de Arquímedes. Para resolverlo, se necesita una ecuación especial que más tarde se llamaría ecuación de Pell. Estas ecuaciones fueron resueltas con éxito por primera vez por matemáticos de la India.
Diofanto de Alejandría
Se sabe poco de Diofanto de Alejandría, quien vivió alrededor del siglo III d.C. Se conservan seis de sus trece libros de la Aritmética en griego y cuatro más en árabe. La Aritmética es una colección de problemas donde se busca encontrar soluciones racionales (fracciones) a ecuaciones con polinomios. Por eso, hoy hablamos de "ecuaciones diofánticas" cuando buscamos soluciones enteras o racionales.
Diofanto estudiaba puntos con coordenadas racionales en curvas. A diferencia de los griegos clásicos, que usaban la geometría para el álgebra, Diofanto usaba el álgebra para la geometría. Su objetivo era encontrar formas de expresar las soluciones de una ecuación usando funciones racionales.
También estudió ecuaciones de algunas curvas más complejas, como las curvas elípticas. Encontró puntos racionales en estas curvas usando un método similar a dibujar una línea tangente a la curva en un punto conocido y encontrar otro punto de intersección.
Diofanto se enfocaba en soluciones racionales, pero también asumió algunas ideas sobre los números enteros, como que todo número entero es la suma de cuatro cuadrados, aunque no lo dijo claramente.
Āryabhaṭa, Brahmagupta, Bhāskara
Las matemáticas indias son una tradición propia, aunque la astronomía griega pudo haber influido. No hay pruebas de que los Elementos de Euclides llegaran a la India antes del siglo XVIII.
Āryabhaṭa (476-550 d.C.) mostró cómo resolver sistemas de ecuaciones con restos, usando un método llamado kuṭṭaka o pulverizador. Este método es parecido al algoritmo euclidiano y probablemente fue descubierto de forma independiente en la India. Āryabhaṭa lo usaba para cálculos astronómicos.
Brahmagupta (628 d.C.) empezó a estudiar las ecuaciones cuadráticas indefinidas, como la Ecuación de Pell. Esta ecuación interesó a Arquímedes y no se resolvió en Occidente hasta la época de Fermat y Euler. Un método general para resolver la ecuación de Pell, llamado chakravala (o "método cíclico"), fue encontrado por Jayadeva y luego por Bhāskara II (siglo XII).
Las matemáticas indias no se conocieron mucho en Europa hasta finales del siglo XVIII. Las obras de Brahmagupta y Bhāskara fueron traducidas al inglés en 1817.
La aritmética en la edad de oro islámica
_(cropped).jpg)
A principios del siglo IX, el califa Al-Ma'mun ordenó traducir muchas obras matemáticas griegas y una sánscrita. La obra principal de Diofanto, la Aritmética, fue traducida al árabe por Qusta ibn Luqa (820-912). Parte del tratado al-Fakhri de al-Karajī (953 - ca. 1029) se basa en ella. Se cree que Ibn al-Haytham, contemporáneo de Al-Karajī, conocía lo que más tarde se llamaría teorema de Wilson.
Europa Occidental en la Edad Media
Durante la Edad Media, no hubo mucho desarrollo en la teoría de números en Europa occidental, salvo un trabajo de Fibonacci sobre cuadrados en progresiones aritméticas. Las cosas empezaron a cambiar en Europa al final del Renacimiento, gracias al estudio de las obras griegas antiguas. Un factor importante fue la traducción al latín de la Arithmetica de Diofanto.
Ramas de la Teoría de Números
La teoría de números se divide en varias ramas, según los métodos que usan y las preguntas que intentan responder.
Teoría elemental de números
Esta rama estudia los números enteros sin usar técnicas de otras áreas de las matemáticas. Incluye temas como la divisibilidad, el algoritmo de Euclides para encontrar el máximo común divisor, la factorización de números en números primos, la búsqueda de números perfectos y las congruencias. Ejemplos importantes son el pequeño teorema de Fermat y el teorema de Euler, el teorema chino del resto y la ley de reciprocidad cuadrática. También se investigan las propiedades de las funciones multiplicativas como la función de Möbius y la función φ de Euler, y secuencias de números como los factoriales y los números de Fibonacci.
Algunas preguntas en la teoría elemental de números parecen sencillas, pero son muy difíciles de responder y requieren ideas nuevas. Por ejemplo:
- La Conjetura de Goldbach: dice que todos los números pares (mayores que 2) son la suma de dos números primos.
- La Conjetura de los números primos gemelos: pregunta si hay infinitos pares de números primos gemelos (primos que se diferencian en 2, como 3 y 5, o 11 y 13).
- El Último teorema de Fermat: fue demostrado en 1995 por Andrew Wiles.
- La Hipótesis de Riemann: trata sobre la distribución de los ceros de la función zeta de Riemann, lo que está relacionado con cómo se distribuyen los números primos.
Teoría analítica de números
Esta rama usa herramientas del cálculo y el análisis complejo para resolver problemas sobre los números enteros. Ejemplos importantes son el teorema de los números primos y la hipótesis de Riemann. Problemas como el problema de Waring, la conjetura de los números primos gemelos y la conjetura de Goldbach también se estudian con métodos analíticos.
Teoría de números aditiva
La teoría de números aditiva se enfoca en cómo se pueden representar los números como sumas de otros números. Problemas como el problema de Waring y la conjetura de Goldbach son típicos aquí. A menudo se usan resultados de la teoría analítica de números, como el método del círculo de Hardy-Littlewood, y a veces se complementa con la teoría de cribas o métodos topológicos.
Teoría algebraica de números
La teoría algebraica de números expande el concepto de número a los números algebraicos. Estos son las raíces de polinomios con coeficientes racionales.
Teoría geométrica de números
La teoría geométrica de números (también llamada geometría de números) usa ideas de la geometría. Comienza con el teorema de Minkowski sobre puntos comunes en conjuntos convexos y el estudio de superficies esféricas.
Teoría combinatoria de números
La teoría combinatoria de números aborda problemas de la teoría de números usando ideas de la combinatoria. Paul Erdős es considerado el creador de esta rama. Los temas incluyen sistemas cubiertos, problemas de suma cero y progresiones aritméticas en conjuntos de enteros. Los métodos algebraicos o analíticos son muy útiles en este campo.
Teoría computacional de números
La teoría computacional de números estudia los algoritmos relacionados con la teoría de números. Los algoritmos rápidos para encontrar números primos y factorizar enteros son muy importantes en la criptografía (el estudio de códigos secretos).
Como dijo Enzo R. Gentile, el avance de la computación ha transformado la aritmética de una ciencia teórica a una rama aplicada. La necesidad de nuevos algoritmos de computación requiere un conocimiento profundo de la aritmética.
Historia (continuación)
Los matemáticos en la India se interesaron en encontrar soluciones enteras para las ecuaciones diofánticas desde mediados del primer milenio a.C. El uso de estas ecuaciones en geometría se remonta a los Shulba-sutras, escritos entre los siglos V y III a.C. El religioso Baudhaiana (siglo IV a.C.) encontró conjuntos de enteros positivos para ecuaciones diofánticas simultáneas. Apastamba (siglo III a.C.) usó ecuaciones diofánticas simultáneas con más de cinco incógnitas.
Los matemáticos yainas fueron los primeros en pensar que no todos los infinitos son iguales. Reconocieron cinco tipos diferentes de infinitos: en una o dos direcciones, en superficies, en todas partes y perpetuamente infinito.
La teoría de números fue muy popular entre los matemáticos griegos de Alejandría (en Egipto) a partir del siglo III a.C. Ellos ya conocían el concepto de ecuación diofántica en casos específicos. El primer matemático helenístico que estudió estas ecuaciones fue Diofanto.
Diofanto investigó un método para encontrar soluciones enteras para las ecuaciones lineales indeterminadas. Estas son ecuaciones que no tienen suficiente información para dar una única respuesta. Por ejemplo, x + y = 5. Diofanto descubrió que muchas ecuaciones indeterminadas se pueden simplificar para encontrar soluciones.
Las ecuaciones diofánticas fueron estudiadas intensamente por los matemáticos hindúes medievales. Ellos fueron los primeros en buscar métodos sistemáticos para encontrar soluciones enteras. Ariabhata (476-550) dio la primera descripción clara de la solución entera general para la ecuación diofántica lineal ay + bx = c en su texto Ariabhatíia. El algoritmo kuttaka de Ariabhata es una de sus contribuciones más importantes. Este algoritmo encuentra soluciones enteras para sistemas de ecuaciones diofánticas lineales, lo cual era muy útil en la astronomía.
Brahmagupta (598-668) trabajó con ecuaciones diofánticas más complejas, como la ecuación de Pell (por ejemplo, 61x² + 1 = y²). Su libro Brahma-sphuta-siddhanta fue traducido al árabe en 773 y al latín en 1126. La ecuación 61x² + 1 = y² fue propuesta como un problema por el matemático francés Pierre de Fermat. La solución general de esta forma de la ecuación de Pell fue encontrada 70 años después por Leonhard Euler, y la solución general de la ecuación de Pell fue encontrada 100 años después por Joseph-Louis de Lagrange en 1767. Sin embargo, siglos antes, Bhaskara II en 1150 ya había trabajado con la ecuación de Pell usando una versión modificada del método chakravala de Brahmagupta. El método chakravala era más simple que el de Lagrange. Bhaskara también encontró soluciones para otras ecuaciones cuadráticas, cúbicas, cuárticas y polinómicas de grados mayores. Naraian Pandit mejoró aún más las soluciones para ecuaciones de grados superiores.
Véase también
En inglés: Number theory Facts for Kids
- Problemas de Hilbert
- Sucesión de Fibonacci
- Número áureo
- Teorema chino del resto
- Sophie Germain
- Números primos de Mersenne y números perfectos
Galería de imágenes
-
La distribución de números primos es un punto central de estudio en la teoría de números. Esta espiral de Ulam sirve para ilustrarlo.
