Factorial para niños

Gráfica de los factoriales del 1 al 5

$n$	$n!$
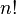0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40.320
9	362.880
10	3.628.800
15	1.307.674.368.000
20	2.432.902.008.176.640.000
25	15.511.210.043.330.985.984.000.000
50	30.414.093.201.713.378.043 × 10⁴⁵
70	1,19785717... × 10¹⁰⁰
450	1,73336873... × 10¹⁰⁰⁰
3.249	6,41233768... × 10^{10 000}
25.206	1,205703438... × 10^{100 000}
100.000	2,8242294079... × 10^{456 573}
205.023	2,5038989316... × 10^{1 000 004}
1.000.000	8,2639316883... × 10^{5 565 708}
10¹⁰⁰	1,6294043324... × 10^10¹⁰¹

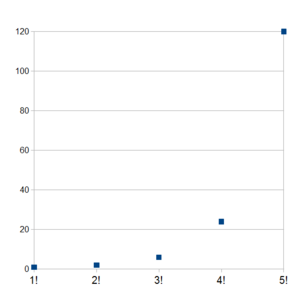
El factorial de un número entero positivo n, que se escribe como n!, es el resultado de multiplicar todos los números enteros positivos desde el 1 hasta ese número n. Por ejemplo, para calcular el factorial de 5:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5! = 1 \times 2 \times 3 \times 4 \times 5 = 120.

Esta operación matemática es muy útil y aparece en muchas áreas de las matemáticas. Se usa especialmente en la combinatoria, que es la parte de las matemáticas que estudia las diferentes formas de organizar o combinar elementos.

Una de las ideas principales del factorial es que nos dice cuántas maneras distintas hay de ordenar n objetos diferentes. Por ejemplo, si tienes 3 libros distintos, ¿de cuántas maneras puedes ordenarlos en una estantería? La respuesta es 3! = 1 × 2 × 3 = 6 maneras.

Los matemáticos han conocido el concepto de factorial desde hace muchos siglos. En el siglo XII, estudiosos de la India ya lo utilizaban. La forma actual de escribir el factorial, n!, fue introducida en 1808 por el matemático francés Christian Kramp.

Contenido

¿Qué es el Factorial y Cómo se Calcula?
- Definición por Multiplicación
- Definición por Recurrencia
  - El Factorial de Cero
Historia del Factorial
- Orígenes Antiguos
- Desarrollo Moderno
Propiedades Importantes del Factorial
Aplicaciones del Factorial
Extensiones del Factorial
Productos Similares al Factorial
- Primorial
- Doble Factorial
Galería de imágenes
Véase también

¿Qué es el Factorial y Cómo se Calcula?

El factorial de un número entero positivo n se define como el producto de todos los números enteros positivos que son menores o iguales que n.

Definición por Multiplicación

La forma más sencilla de entender el factorial es como una multiplicación en cadena:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n! = 1 \times 2 \times 3 \times \dots \times (n-1) \times n .

También se puede escribir usando un símbolo especial de multiplicación llamado productoría:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n! = \prod_{k=1}^n k .

Definición por Recurrencia

Otra forma de definir el factorial es usando una regla que se repite, llamada relación de recurrencia:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n! = \begin{cases} 1 & \text{si, } n < 2 \\ (n-1)!\times n & \text{si, } n > 1 \end{cases}

Esta regla significa que para calcular el factorial de un número, multiplicas ese número por el factorial del número anterior.

El Factorial de Cero

Según la definición por recurrencia, el factorial de 0 (cero) se define como 1. Esto puede parecer extraño al principio, pero tiene una razón importante en matemáticas.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0! = 1

Para entender por qué 0! es 1, podemos usar la regla de recurrencia al revés. Si sabemos que 5! es 120, entonces 4! es 120 dividido por 5, que es 24.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{5!}{5} = \frac{120}{5} = 24

Si seguimos este patrón:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1! = \frac{2!}{2} = \frac{2}{2} = 1

Aplicando la misma lógica para 0!:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0! = \frac{1!}{1} = \frac{1}{1} = 1

Aunque este es un argumento útil, la razón principal por la que 0! es 1 es una convención matemática llamada "producto vacío", que se usa en muchas otras áreas de las matemáticas.

Historia del Factorial

El concepto de factorial ha aparecido de forma independiente en diferentes culturas a lo largo de la historia.

Orígenes Antiguos

En las matemáticas indias, una de las primeras menciones de los factoriales se encuentra en el Anuyogadvāra-sūtra, un texto antiguo que data de entre el 300 a.C. y el 400 d.C. También el monje jainista Jinabhadra, en el siglo VI, describió reglas para las permutaciones. Más tarde, en 1150, Bhāskara II usó factoriales en su obra Līlāvatī para resolver problemas de combinaciones.
En las matemáticas de Oriente Medio, el libro místico hebreo Séfer Ietzirá, del período talmúdico (200 a 500 d.C.), menciona factoriales hasta 7! para explorar cuántas palabras se pueden formar con el alfabeto hebreo. El matemático árabe Ibn al-Haytham (conocido como Alhazen, alrededor del año 965-1040) fue el primero en formular el teorema de Wilson, que relaciona los factoriales con los números primos.
En Europa, aunque los griegos antiguos no estudiaron los factoriales directamente, el filósofo Platón usó el número 5040 (que es 7!) como la población ideal de una comunidad, en parte por sus propiedades de divisibilidad. El primer trabajo sobre factoriales en Europa fue realizado por estudiosos judíos que explicaban el pasaje del Séfer Ietzirá. En 1677, el autor británico Fabian Stedman describió cómo los factoriales se aplicaban al "toque de cambios", un arte musical con campanas.

Desarrollo Moderno

A partir de finales del siglo XV, los factoriales se convirtieron en un tema de estudio para los matemáticos occidentales.

En 1494, el matemático italiano Luca Pacioli calculó factoriales hasta 11! para un problema de organización de mesas.
En 1676, Isaac Newton formuló la serie de potencias para la función exponencial, que usa los inversos de los factoriales.
Matemáticos como Abraham de Moivre y James Stirling estudiaron cómo aproximar los factoriales para números muy grandes, lo que llevó a la famosa aproximación de Stirling.
Daniel Bernoulli y Leonhard Euler extendieron la idea del factorial a una función continua para números no enteros, conocida como la función gamma.
La notación n! fue introducida por Christian Kramp en 1808. La palabra "factorial" (originalmente en francés: factorielle) fue usada por primera vez en 1800 por Louis François Antoine Arbogast.

Propiedades Importantes del Factorial

Los factoriales tienen algunas propiedades interesantes:

Si tienes dos números enteros positivos, m y n, y m es menor que n, entonces el factorial de m siempre será menor que el factorial de n.
Si m es menor que n, el factorial de m es un factor (o divisor) del factorial de n. Esto significa que n! se puede escribir como: n! = n(n-1)...(m+1).m!
Para números n mayores que 1, el factorial de n es menor que el resultado de elevar a n la mitad de n más 1.

Aplicaciones del Factorial

Los factoriales son fundamentales en varias ramas de las matemáticas:

Combinatoria y Probabilidad

Se usan mucho en la combinatoria para calcular el número de formas de organizar o seleccionar elementos. Por ejemplo, en el binomio de Newton, que es una fórmula para desarrollar expresiones como (a + b)ⁿ, los factoriales ayudan a encontrar los coeficientes:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a+b)^n = {n\choose 0}a^n + {n\choose 1} a^{n-1} b + {n \choose 2} a^{n-2}b^2 + \cdots + {n\choose n}b^n = \sum_{k=0}^n {n \choose k} a^{n-k} b^{k}

Donde ${n \choose k}$ se calcula con factoriales:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {n\choose k} = \frac{n!}{(n - k)! \cdot k!}

Gracias a la combinatoria, los factoriales también son clave para calcular probabilidades.

Análisis Matemático

En el análisis matemático, los factoriales aparecen en el desarrollo de funciones en series, como la fórmula de Taylor, que permite aproximar funciones con polinomios.

Aproximación de Stirling

Para calcular factoriales de números muy grandes, existe una fórmula aproximada llamada fórmula de Stirling:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n!\approx \sqrt{2 \pi n} \left (\frac{n}{e} \right )^{n} \left (1+\frac{1}{12n}+\frac{1}{288n^2}+\cdots \right )

Esta fórmula es muy útil porque no necesita calcular todos los productos uno por uno, lo que la hace mucho más rápida para números grandes.

Extensiones del Factorial

Gráfica de la función factorial extendida

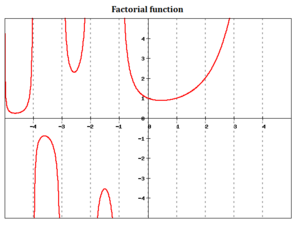
La definición de factorial que hemos visto es para números enteros no negativos. Sin embargo, los matemáticos han logrado extender esta idea a otros tipos de números, como los números reales y los números complejos, excepto para los enteros negativos.

Esta extensión se realiza a través de una función muy importante llamada función gamma, que se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(n) . Para números positivos, la función gamma se relaciona con el factorial de la siguiente manera:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(n) = (n-1)!

Productos Similares al Factorial

Existen otras operaciones matemáticas que se parecen al factorial:

Primorial

El primorial se define de forma similar al factorial, pero en lugar de multiplicar todos los números hasta n, solo se multiplican los números primos que son menores o iguales que n:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n\# = \prod_{p \le n\atop p \text{ primo}} p .

Por ejemplo, 7# (primorial de 7) sería 2 × 3 × 5 × 7 = 210.

Doble Factorial

El doble factorial de n, que se escribe n!!, se define de una manera especial:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\textstyle n!! = \left \{ \begin{array}{lcl} 1 & \mbox{si} & n = 0 \\ (n-2)!! \cdot n & \mbox{si} & n \ne 0 \end{array} \right .}

Esto significa que si n es par, multiplicas todos los números pares hasta n. Si n es impar, multiplicas todos los números impares hasta n. Por ejemplo:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 8!! = 2 \cdot 4 \cdot 6 \cdot 8 = 384

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 9!! = 1 \cdot 3 \cdot 5 \cdot 7 \cdot 9 = 945

La secuencia de dobles factoriales comienza así: 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, ...

Galería de imágenes

Gráfica de la función factorial extendida

Véase también

En inglés: Factorial Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Factorial&oldid=4961388»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Factorial para Niños. Enciclopedia Kiddle.