Aritmética modular para niños

Enciclopedia para niños

La aritmética modular es una parte de las matemáticas que nos ayuda a resolver problemas con números enteros. Se basa en estudiar los restos que obtenemos al hacer una división. Fue presentada por primera vez en 1801 por un matemático muy famoso llamado Carl Friedrich Gauss en su libro Disquisitiones arithmeticae.

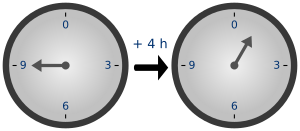
Un ejemplo muy común de la aritmética modular es el reloj de 12 horas. Si son las 7:00 y pasan 8 horas, no decimos que son las 15:00. En el reloj, las 15:00 se leen como las 3:00. Esto es porque el reloj "vuelve a empezar" cada 12 horas. Decimos que 15 es "congruente" con 3 "módulo" 12. Esto se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 15 \equiv 3 (\bmod 12) . De la misma forma, si multiplicamos 8 horas por 2, obtenemos 16 horas, que en el reloj se leen como 4:00. Esto se escribe: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2\cdot8\equiv 4(\bmod 12) .

¿Qué es la congruencia?

El tiempo en este reloj usa aritmética en módulo 12.

La aritmética modular se construye usando una idea llamada "relación de congruencia" entre números enteros. Esta relación funciona bien con las operaciones de suma y multiplicación.

Para un número especial llamado "módulo" (que se escribe como $n$ ), decimos que dos números, por ejemplo, a y b, son congruentes si:

Ambos números dejan el mismo resto cuando los dividimos entre $n$ .
O, de forma equivalente, si la resta de a menos b (a − b) es un múltiplo de $n$ .

Esta relación se escribe de una forma especial que usó Gauss:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv b(\bmod n)

Por ejemplo:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 63\equiv 83 (\bmod10)

Esto es cierto porque tanto 63 como 83, al dividirlos entre 10, dejan el mismo resto, que es 3. O, si restamos 63 − 83, obtenemos -20, y -20 es un múltiplo de 10.

Se lee: "63 es congruente con 83, módulo 10". La palabra "módulo" a veces se abrevia como "mod" y viene del latín modulus. El número $n$ (en este ejemplo, 10) es el "módulo".

Otro ejemplo: si el módulo es 12, cualquier par de números que al dividirlos entre 12 den el mismo resto, son congruentes. Los números: ..., −34, −22, −10, 2, 14, 26,... Todos estos números son "congruentes módulo 12" entre sí, porque cada uno deja el mismo resto (2) cuando los dividimos entre 12.

Propiedades importantes

Grupos de números congruentes

La aritmética modular agrupa los números que se comportan de forma similar. Por ejemplo, todos los números que dejan el mismo resto al dividirlos por un módulo $n$ forman un grupo.

Esta relación de congruencia tiene propiedades importantes: Si tenemos:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1\equiv b_1(\bmod n)

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_2\equiv b_2(\bmod n)

Entonces:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1+a_2\equiv b_1+b_2 (\bmod n) (Podemos sumar números congruentes)

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1\cdot a_2\equiv b_1\cdot b_2(\bmod n) (Podemos multiplicar números congruentes)

Esto significa que la suma y la multiplicación funcionan bien con estos grupos de números. Por ejemplo, en el sistema módulo 12: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [8]_{12}\cdot[3]_{12} + [6]_{12} = [30]_{12} =[6]_{12} Esto es como decir: (8 por 3) más 6 es igual a 30. Y 30, en un reloj de 12 horas, es como 6.

Resolver ecuaciones de congruencia

Una ecuación de congruencia se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax\equiv b (\bmod n) . Queremos encontrar el valor de $x$ . Esta ecuación tiene solución si el máximo común divisor de $a$ y $n$ divide a $b$ .

A veces, un número $a$ tiene un "inverso multiplicativo" en aritmética modular. Esto significa que hay otro número que, al multiplicarlo por $a$ , el resultado es 1 (módulo $n$ ). Esto solo ocurre si $a$ y $n$ no tienen factores comunes (son coprimos).

Teoremas importantes: Fermat y Euler

Hay dos teoremas muy importantes en aritmética modular, especialmente cuando el módulo es un número primo:

Pequeño teorema de Fermat: Si 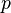$p$ es un número primo, entonces para cualquier número natural $a$ :

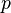:Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^p \equiv a(\bmod p) Si $a$ no es divisible por $p$ , entonces: :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{p-1} \equiv 1(\bmod p)

Teorema de Euler: Este teorema es una versión más general del teorema de Fermat. Dice que si $a$ y $n$ no tienen factores comunes, entonces:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{\phi(n)}\equiv1(\bmod n) Aquí, 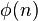$\phi(n)$ es la función phi de Euler, que cuenta cuántos números entre 1 y $n$ son coprimos con $n$ .

Reglas básicas de la congruencia

Aquí hay algunas reglas que siempre se cumplen en aritmética modular:

Reflexividad: Cualquier número es congruente consigo mismo. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv a(\bmod n)
Simetría: Si $a$ es congruente con $b$ , entonces $b$ es congruente con $a$ . Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv b(\bmod n) , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b\equiv a (\bmod n) .
Transitividad: Si $a$ es congruente con $b$ , y $b$ es congruente con $c$ , entonces $a$ es congruente con $c$ . Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv b(\bmod n) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b\equiv c (\bmod n) , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv c(\bmod n) .

Estas propiedades hacen que la congruencia sea una "relación de equivalencia".

Más propiedades de las operaciones

Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv b (\bmod n) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c\equiv d (\bmod n) , entonces:

Podemos multiplicar por un número: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lambda a\equiv\lambda b (\bmod n)
Podemos sumar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a+c\equiv b+d (\bmod n)
Podemos multiplicar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ac\equiv bd (\bmod n)

También, si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\equiv b (\bmod n) , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^k\equiv b^k (\bmod n) para cualquier número entero positivo 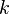$k$ .

Criterios de divisibilidad

La aritmética modular nos ayuda a entender las reglas de divisibilidad. Si tenemos un número $n$ (por ejemplo, 12345), podemos saber si es divisible por otros números sin hacer la división completa:

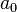Divisible por 2: $n$ es divisible por 2 si su último dígito ( $a_0$ ) es divisible por 2.
Divisible por 3: $n$ es divisible por 3 si la suma de sus dígitos es divisible por 3.
Divisible por 4: $n$ es divisible por 4 si el número formado por sus dos últimos dígitos es divisible por 4.
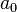Divisible por 5: $n$ es divisible por 5 si su último dígito ( $a_0$ ) es 0 o 5.
Divisible por 9: $n$ es divisible por 9 si la suma de sus dígitos es divisible por 9.
Divisible por 11: $n$ es divisible por 11 si la suma alternada de sus dígitos (último dígito - penúltimo + antepenúltimo...) es divisible por 11.

Aplicaciones de la aritmética modular

La aritmética modular, que Carl Friedrich Gauss estudió a finales del siglo XVIII, se usa en muchas áreas:

En computación

Muchas de las operaciones que hacen las computadoras hoy en día son aritméticas modulares. Por ejemplo, cuando una computadora trabaja con números enteros, a menudo lo hace "módulo" una potencia de 2 (como 2³²), que es el número de bits que usa para guardar esos números.

En seguridad digital (criptografía)

La aritmética modular es muy importante en la criptografía, que es el arte de proteger la información. Permite crear sistemas de cifrado muy seguros, como el sistema RSA, que ayudan a mantener nuestras comunicaciones y datos privados en internet.

En el arte

Música: En música, la aritmética modular se usa para entender las escalas y las notas. Por ejemplo, en la escala de doce tonos, las octavas son equivalentes (una nota se repite más aguda o más grave), y esto se puede ver con la aritmética modular.
Artes visuales: También se puede usar para crear patrones artísticos basados en tablas de multiplicación módulo $n$ .

Galería de imágenes

Cubierta de la edición original de Disquisitiones arithmeticae de Gauss, libro fundamental de la aritmética.

Ver también

Véase también

En inglés: Modular arithmetic Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Aritmética_modular&oldid=4831824»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Aritmética modular para Niños. Enciclopedia Kiddle.