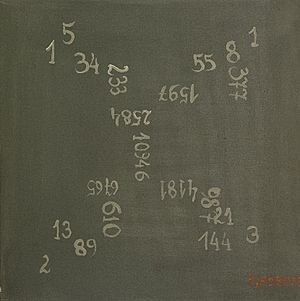Sucesión de Fibonacci para niños
La sucesión de Fibonacci es una lista especial de números donde cada número es la suma de los dos anteriores. ¡Es como un patrón matemático que se repite!
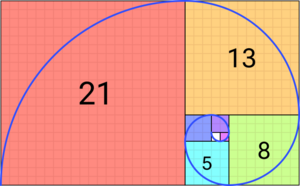
La sucesión comienza así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597...
Esta secuencia fue explicada en Europa por Leonardo de Pisa, un matemático italiano del siglo XIII al que también se le conoce como Fibonacci. La sucesión de Fibonacci tiene muchas aplicaciones en diferentes campos, como la informática, las matemáticas, las tendencias del mercado financiero y la teoría de juegos.
También aparece en la naturaleza, por ejemplo, en cómo se ramifican los árboles, en la forma en que las hojas crecen en un tallo, en las flores de las alcachofas y los girasoles, en las piñas de los árboles, en la forma de algunos caparazones de animales como el nautilus, en la estructura de las galaxias y hasta en las proporciones del cuerpo humano.
Contenido
Historia de la Sucesión de Fibonacci
La sucesión fue presentada en Occidente por Fibonacci. Él la explicó usando un problema sobre cómo se reproducen los conejos, lo que dio origen a la idea de que así la descubrió.
Leonardo Pisano, conocido como Fibonacci, nació en 1170 y falleció en 1240. Él fue un gran estudioso de las matemáticas que aprendió en ciudades del sur del Mediterráneo, como Alejandría y Argelia. Compartió muchos usos prácticos de las matemáticas que no se conocían en Occidente, como los números arábigos (con un sistema decimal y el número cero). La República de Pisa le pagaba un salario por sus consejos en contabilidad y por enseñar a sus ciudadanos.
Antes de que se conociera en Europa, la sucesión de Fibonacci ya había sido descrita en la matemática en la India, relacionada con la poesía sánscrita.
Algunos expertos, como Susantha Goonatilake, creen que el desarrollo de la secuencia de Fibonacci se atribuye en parte a Pingala (alrededor del año 200), y más tarde a Virahanka (hacia el año 700), Gopāla (hacia 1135) y Hemachandra (hacia 1150).
El problema de los conejos
Fibonacci usó este ejemplo para explicar su sucesión: Imagina que tienes una pareja de conejos recién nacidos.
- Los conejos tardan un mes en madurar.
- Después de ese mes, cada pareja madura tiene otra pareja de conejos cada mes.
- Los conejos nunca mueren.
Veamos cómo crece la población de conejos mes a mes:
| Número de mes | Explicación | Parejas de conejos |
|---|---|---|
| Comienzo del mes 1 | Nace una pareja de conejos (pareja A). | 1 pareja |
| Fin del mes 1 | La pareja A tiene un mes y se cruza. | 1 pareja |
| Fin del mes 2 | La pareja A tiene una nueva pareja (B). La pareja A se vuelve a cruzar. | 2 parejas |
| Fin del mes 3 | La pareja A tiene otra pareja (C). La pareja B tiene un mes y se cruza. | 3 parejas |
| Fin del mes 4 | Las parejas A y B tienen nuevas parejas (D y E). La pareja C tiene un mes y se cruza. | 5 parejas |
| Fin del mes 5 | A, B y C tienen nuevas parejas (F, G y H). D y E tienen un mes y se cruzan. | 8 parejas |
| Fin del mes 6 | A, B, C, D y E tienen nuevas parejas (I, J, K, L y M). F, G y H tienen un mes y se cruzan. | 13 parejas |
Como puedes ver, el número de parejas de conejos en cada mes sigue la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13...
Fibonacci presentó esta sucesión en su libro Liber Abaci, publicado en 1202. Muchas de las características de la sucesión de Fibonacci fueron descubiertas por Édouard Lucas, quien le dio el nombre que conocemos hoy.
Otros matemáticos como Johannes Kepler también describieron los números de Fibonacci. El matemático escocés Robert Simson descubrió en 1753 que la relación entre dos números consecutivos de Fibonacci (por ejemplo, 89 dividido por 55) se acerca al Número áureo (un número especial que se representa con la letra griega phi, 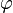 ) a medida que los números se hacen más grandes.
) a medida que los números se hacen más grandes.
¿Cómo se define la Sucesión de Fibonacci?
Los números de Fibonacci se definen con estas reglas:
(1)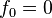
(2)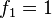
(3)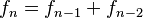
Esto significa que para encontrar cualquier número de la sucesión (llamado 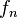 ), debes sumar los dos números que lo preceden. Por ejemplo, para encontrar
), debes sumar los dos números que lo preceden. Por ejemplo, para encontrar 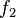 , sumas
, sumas 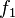 y
y 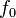 (1 + 0 = 1).
(1 + 0 = 1).
Así se obtienen los primeros números:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_2 = 1 (0 + 1)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_3 = 2 (1 + 1)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_4 = 3 (1 + 2)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_5 = 5 (2 + 3)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_6 = 8 (3 + 5)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_7 = 13 (5 + 8)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_8 = 21 (8 + 13)
¡Y así sigue!
Fórmula explícita
Aunque la forma más sencilla de entender la sucesión es sumando los dos números anteriores, existe una fórmula especial que te permite calcular cualquier número de Fibonacci directamente, sin tener que calcular todos los anteriores. Esta fórmula se llama fórmula de Binet:
(5)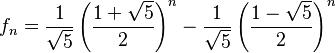
Esta fórmula usa el número áureo (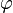 ), que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1+\sqrt5}2 . Aunque los números de Fibonacci son números enteros, esta fórmula usa números con decimales y raíces cuadradas. ¡Es sorprendente cómo se conectan!
), que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1+\sqrt5}2 . Aunque los números de Fibonacci son números enteros, esta fórmula usa números con decimales y raíces cuadradas. ¡Es sorprendente cómo se conectan!
Propiedades de la Sucesión
Los números de Fibonacci tienen muchas propiedades interesantes:
- Relación con el número áureo: Si divides un número de Fibonacci por el número anterior (por ejemplo, 89/55), el resultado se acerca cada vez más al número áureo (
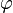 ), que es aproximadamente 1.618.
), que es aproximadamente 1.618. - Suma de términos: Cualquier número natural se puede escribir sumando diferentes números de Fibonacci. Por ejemplo, 17 = 13 + 3 + 1.
- Pares e impares: Solo uno de cada tres números de Fibonacci es par.
- Divisibilidad: El máximo común divisor de dos números de Fibonacci es otro número de Fibonacci. Por ejemplo, el máximo común divisor de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_6 (que es 8) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_9 (que es 34) es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_3 (que es 2).
- Triángulo de Pascal: Los números de Fibonacci aparecen si sumas las diagonales del triángulo de Pascal.

Generalización de Fibonacci
El concepto principal de la sucesión de Fibonacci es que cada número es la suma de los dos anteriores. Esta idea se puede extender a otros números, no solo a los que empiezan con 0 y 1.
Una sucesión de Fibonacci generalizada es cualquier sucesión donde cada número es la suma de los dos anteriores, pero no necesariamente empieza con 0 y 1.
Sucesión de Lucas
Un ejemplo importante de una sucesión de Fibonacci generalizada es la sucesión de Lucas. Esta sucesión comienza con 2 y 1:

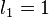
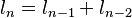 (igual que Fibonacci, cada número es la suma de los dos anteriores)
(igual que Fibonacci, cada número es la suma de los dos anteriores)
La sucesión de Lucas es: 2, 1, 3, 4, 7, 11, 18, 29... También se relaciona con el número áureo y comparte muchas características con la sucesión de Fibonacci.
Cómo calcular los números de Fibonacci
Existen diferentes maneras de calcular un número específico de la sucesión de Fibonacci.
Método recursivo
La forma más directa de escribir un programa para calcular un número de Fibonacci es usando su propia definición:
| Algoritmo 1 Versión recursiva |
|
función
|
Este método es simple de entender, pero puede ser muy lento para números grandes, ya que calcula muchas veces los mismos valores.
Método iterativo
Un método más eficiente es el iterativo, que va calculando los números uno por uno, guardando solo los dos últimos valores.
| Algoritmo 3 Versión iterativa |
|
función
|
Este método es mucho más rápido que el recursivo para calcular números grandes.
La Sucesión de Fibonacci en la Naturaleza
La secuencia de Fibonacci aparece en muchas formas en la naturaleza. Por ejemplo, en cómo se distribuyen las ramas de los árboles, en la forma en que las hojas crecen en un tallo (llamado Filotaxis), en los frutos de la piña tropical, en las flores de la alcachofa, en las piñas de los árboles, y en el "árbol genealógico" de las abejas.
Un ejemplo muy conocido es el patrón de las semillas del girasol. Las semillas se organizan en espirales que siguen los números de Fibonacci. A menudo se dice que los girasoles tienen 55 espirales en una dirección y 89 en otra (o alguna otra pareja de números consecutivos de Fibonacci).
El árbol genealógico de las abejas
Los machos de una colmena de abejas, llamados zánganos, tienen un árbol genealógico que sigue la sucesión de Fibonacci.
- Un zángano (1) no tiene padre, solo madre.
- Su madre (1) tiene dos padres (1, 1).
- Esos dos padres (los abuelos del zángano) tienen tres padres en total (1, 1, 2).
- Y así sucesivamente, el número de antepasados sigue la secuencia: 1, 1, 2, 3, 5, 8...
Algunos historiadores sugieren que Fibonacci pudo haberse inspirado en el conocimiento de los criadores de abejas de la ciudad de Bejaia (que era un importante centro de exportación de cera en su época) para descubrir estos números, más que en el problema de los conejos.
La Sucesión de Fibonacci en la Cultura Popular
- En la novela Rama II (novela) de Arthur C. Clarke, un personaje la menciona como una forma de recordar una clave secreta larga, por lo fácil que es extenderla.
- En el popular anime y manga JoJo's Bizarre Adventure, específicamente en Steel Ball Run, la sucesión de Fibonacci se relaciona con cómo los poderes de los personajes se hacen más fuertes, mencionada como el "Rectángulo dorado".
Véase también
 En inglés: Fibonacci sequence Facts for Kids
En inglés: Fibonacci sequence Facts for Kids
- Número áureo
- Sucesión (matemática)
- Espiral logarítmica
- Número de Lucas


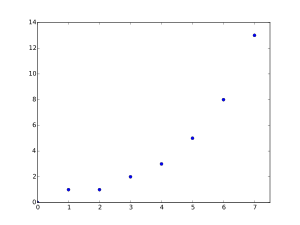

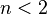 entonces
entonces
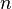



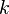 desde
desde 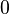 hasta
hasta 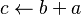


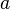

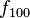 usando el algoritmo iterativo.
usando el algoritmo iterativo.