Teorema de Wilson para niños
El teorema de Wilson es una regla matemática muy interesante que nos ayuda a saber si un número es primo. Un número primo es aquel que solo se puede dividir exactamente por 1 y por sí mismo (como 2, 3, 5, 7...).
Este teorema dice lo siguiente:
|
¿Qué significa (p − 1)!? Es el factorial de (p − 1). El factorial de un número es el resultado de multiplicar ese número por todos los números enteros positivos menores que él hasta llegar a 1. Por ejemplo, 4! (cuatro factorial) es 4 × 3 × 2 × 1 = 24.
Y ¿qué significa "es como -1 cuando lo dividimos por p"? Esto se llama aritmética modular o "módulo". Significa que si dividimos (p − 1)! entre p, el resto que obtenemos es el mismo que si dividiéramos -1 entre p. Por ejemplo, si p es 5, entonces (5-1)! = 4! = 24. Si dividimos 24 entre 5, el resto es 4. Y si dividimos -1 entre 5, el resto también es 4 (porque -1 + 5 = 4). ¡Es como si 4 y -1 fueran lo mismo en el mundo del módulo 5!
Lo más genial es que esta regla funciona al revés también: si un número n (mayor que 1) cumple que (n − 1)! es como -1 cuando lo dividimos por n, ¡entonces n es un número primo!
Contenido
¿Quién descubrió el Teorema de Wilson?
Este teorema fue mencionado por Edward Waring en 1770, quien dijo que John Wilson lo había encontrado. Sin embargo, no hay pruebas de que Wilson lo haya demostrado. La primera persona que sí lo demostró fue Lagrange en 1771.
Pero, en realidad, el teorema fue formulado mucho antes, a principios del siglo XI, por un matemático llamado Abu 'Ali al-Hasan ibn al-Haytham, conocido en Occidente como Alhazen.
Ejemplos del Teorema de Wilson
Vamos a ver cómo funciona el teorema con algunos números. La siguiente tabla muestra el valor de n, el factorial de (n-1), y el resto cuando dividimos (n-1)! entre n.
- Los números primos tienen un fondo rosa.
- Los números compuestos (los que no son primos) tienen un fondo verde claro.
Fíjate que cuando n es primo, el resto siempre es n-1 (que es lo mismo que -1 en el mundo del módulo n).
| n>1 |  |
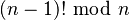 |
|---|---|---|
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 6 | 2 |
| 5 | 24 | 4 |
| 6 | 120 | 0 |
| 7 | 720 | 6 |
| 8 | 5040 | 0 |
| 9 | 40320 | 0 |
| 10 | 362880 | 0 |
| 11 | 3628800 | 10 |
| 12 | 39916800 | 0 |
| 13 | 479001600 | 12 |
| 14 | 6227020800 | 0 |
| 15 | 87178291200 | 0 |
| 16 | 1307674368000 | 0 |
| 17 | 20922789888000 | 16 |
| 18 | 355687428096000 | 0 |
| 19 | 6402373705728000 | 18 |
| 20 | 121645100408832000 | 0 |
| 21 | 2432902008176640000 | 0 |
| 22 | 51090942171709440000 | 0 |
| 23 | 1124000727777607680000 | 22 |
| 24 | 25852016738884976640000 | 0 |
| 25 | 620448401733239439360000 | 0 |
| 26 | 15511210043330985984000000 | 0 |
| 27 | 403291461126605635584000000 | 0 |
| 28 | 10888869450418352160768000000 | 0 |
| 29 | 304888344611713860501504000000 | 28 |
| 30 | 8841761993739701954543616000000 | 0 |
¿Cómo se demuestra el Teorema de Wilson?
Los matemáticos usan diferentes formas para demostrar que este teorema es cierto. Una forma es usando la aritmética modular. Otra forma es usando la teoría de grupos, que es una rama de las matemáticas que estudia conjuntos con operaciones especiales. También se puede demostrar usando polinomios.
La idea principal de las demostraciones es que, si un número p es primo, todos los números entre 1 y p-1 tienen un "compañero" con el que, al multiplicarse, dan un resto de 1 cuando se dividen por p. Solo el 1 y el p-1 son sus propios compañeros. Cuando multiplicas todos los números desde 1 hasta p-1, todos esos "compañeros" se cancelan, dejando solo 1 y p-1, lo que resulta en p-1 (o -1 en módulo p).
Si un número n no es primo (es decir, es compuesto), entonces tiene divisores además de 1 y de sí mismo. Estos divisores harían que (n-1)! fuera divisible por n, y no dejaría un resto de n-1 (o -1).
El inverso del Teorema de Wilson
El inverso del teorema de Wilson dice que si un número n (mayor que 5 y compuesto) divide a (n − 1)!, entonces n no puede ser primo.
Por ejemplo, para n = 4 (que es compuesto), 3! = 6. Si dividimos 6 entre 4, el resto es 2, no 3 (que sería -1 mod 4). Esto confirma que 4 no es primo.
¿Para qué sirve el Teorema de Wilson?
Aunque el teorema de Wilson es muy interesante, no se usa mucho en la práctica para saber si un número muy grande es primo. Esto se debe a que calcular el factorial de un número grande (como 1000!) es una operación que lleva mucho tiempo y recursos en una computadora. Existen otras pruebas de primalidad que son mucho más rápidas y eficientes.
Sin embargo, el teorema de Wilson es una herramienta importante en la teoría de números y ha ayudado a los matemáticos a entender mejor las propiedades de los números primos.
Generalizaciones
El teorema de Wilson se puede extender a otros casos más complejos. Por ejemplo, el famoso matemático Carl Friedrich Gauss mostró una versión más general en su libro Disquisitiones Arithmeticae. Esta versión más avanzada considera el producto de todos los números menores que n que no comparten divisores con n (aparte del 1).
Véase también
 En inglés: Wilson's theorem Facts for Kids
En inglés: Wilson's theorem Facts for Kids

