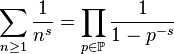Función zeta de Riemann para niños
La función zeta de Riemann (también conocida como dseta, por la letra griega ζ que la representa) es una función matemática muy importante. Fue nombrada en honor al matemático Bernhard Riemann. Es fundamental en la teoría de números porque nos ayuda a entender cómo se distribuyen los números primos. También se usa en otras áreas como la física y la teoría de probabilidades.
Contenido
¿Qué es la función zeta de Riemann?
La función zeta de Riemann, escrita como ζ(s), se define para ciertos números complejos (números que tienen una parte real y una parte imaginaria). Se calcula sumando una serie infinita de fracciones:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \zeta(s) = \frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \ldots
Esta suma funciona bien cuando la parte real del número s es mayor que uno. Riemann descubrió que esta función se puede extender para casi todos los números complejos, excepto para s = 1. Esta extensión es la que se estudia en la famosa hipótesis de Riemann.
¿Cómo se relaciona con los números primos?
La conexión entre esta función y los números primos fue descubierta por primera vez por el matemático Leonhard Euler. Él se dio cuenta de que la suma infinita de la función zeta se puede escribir como un producto infinito que solo usa números primos.
Imagina que multiplicas fracciones como estas:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left(1 + \frac{1}{2^s} + \frac{1}{4^s} + \cdots \right) \times \left(1 + \frac{1}{3^s} + \frac{1}{9^s} + \cdots \right) \times \cdots
Cada paréntesis representa una serie geométrica para un número primo (2, 3, 5, etc.). Cuando multiplicas todas estas series, obtienes la misma suma que la función zeta.
Esto significa que:
Donde el símbolo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle \prod significa que multiplicamos por todos los números primos p. Esta relación se llama el producto de Euler. Es muy importante porque une una suma infinita con los números primos, que son los "ladrillos" de todos los números.
Propiedades importantes
Algunos valores especiales
Euler encontró una fórmula para calcular el valor de ζ(s) cuando s es un número par positivo. Por ejemplo:
- ζ(2) = π²/6 (aproximadamente 1.645)
- ζ(4) = π⁴/90 (aproximadamente 1.082)
Para números impares, como ζ(3), no se conoce una fórmula general sencilla. El valor de ζ(3) es aproximadamente 1.202 y se conoce como la constante de Apéry.
Cuando s es un número negativo par (como -2, -4, -6...), la función zeta de Riemann es igual a cero. A estos se les llama ceros triviales.
- ζ(-1) = -1/12
- ζ(1) es un caso especial, ya que la suma se vuelve infinita.
Ecuación funcional
La función zeta de Riemann se puede calcular para casi cualquier número complejo usando una fórmula especial llamada la ecuación funcional. Esta ecuación fue demostrada por Bernhard Riemann en 1859. Es una herramienta poderosa para entender la función fuera de su definición original.
¿Qué son los ceros de la función?
Los "ceros" de una función son los valores de s para los cuales la función zeta es igual a cero. Ya mencionamos los ceros triviales (los números pares negativos).
Además de estos, existen otros ceros llamados ceros no triviales. Estos ceros son mucho más difíciles de encontrar y se encuentran en una región especial del plano complejo. El estudio de dónde se encuentran estos ceros es muy importante porque nos da pistas sobre cómo se distribuyen los números primos.
La hipótesis de Riemann es uno de los problemas matemáticos más grandes y sin resolver. Esta hipótesis dice que todos los ceros no triviales de la función zeta de Riemann se encuentran en una línea específica en el plano complejo, llamada la recta crítica. Si esta hipótesis fuera cierta, tendría un impacto enorme en la teoría de números.
Se sabe que hay infinitos ceros en la recta crítica, un hecho demostrado por matemáticos como G.H. Hardy y Littlewood.
Aplicaciones de la función zeta
Aunque la función zeta de Riemann es un tema de matemáticas "puras", también tiene usos en otras áreas como la estadística y la física.
Por ejemplo, en física, a veces se necesita sumar números infinitos, como 1 + 2 + 3 + 4 + ... Sorprendentemente, en algunos casos, se espera que el resultado sea un número finito. Aquí es donde la función zeta de Riemann puede ayudar. Usando un método especial llamado "sumación de Ramanujan", se puede asignar un valor finito a estas sumas infinitas. Por ejemplo, la suma 1 + 2 + 3 + ... se puede relacionar con ζ(-1), que es -1/12.
La función zeta también se usa en la física teórica para manejar ciertas sumas infinitas que aparecen en los cálculos.
Generalizaciones de la función zeta
Existen otras funciones que son similares a la función zeta de Riemann o que se basan en ella. Algunas de estas son:
- La función zeta de Hurwitz: Es una versión más general que la función zeta de Riemann.
- El polilogaritmo: Otra función que se relaciona con la zeta de Riemann en un caso particular.
- La función zeta de Lerch: Una función aún más general que incluye las dos anteriores.
También hay otras funciones zeta más complejas, como las funciones L de Dirichlet y las Función zeta de Dedekind, que se usan para estudiar propiedades más avanzadas de los números.
Galería de imágenes
-
Esta imagen muestra un gráfico polar de la función zeta de Riemann a lo largo de la recta crítica para valores de t comprendidos entre 0 y 34. Los cinco primeros ceros son claramente visibles, puesto que corresponden al paso de la espiral por el origen.
Véase también
 En inglés: Riemann zeta function Facts for Kids
En inglés: Riemann zeta function Facts for Kids