Algoritmo de Euclides para niños
El algoritmo de Euclides es un método muy útil en matemáticas para encontrar el Máximo Común Divisor (MCD) de dos números enteros. El MCD es el número más grande que puede dividir a ambos números sin dejar ningún resto. Este algoritmo fue descrito por primera vez por el antiguo matemático griego Euclides en su famoso libro Elementos, hace más de 2300 años (alrededor del 300 a. C.).
Un algoritmo es como una receta o un conjunto de pasos claros para resolver un problema. El algoritmo de Euclides es uno de los algoritmos más antiguos que todavía se usan hoy en día. Es muy importante porque nos ayuda a simplificar fracciones y es la base de muchos cálculos en la teoría de números y en la criptografía, que es la ciencia de proteger la información.
El algoritmo funciona porque el MCD de dos números no cambia si reemplazamos el número más grande por la diferencia entre los dos números. Por ejemplo, el MCD de 252 y 105 es 21. Si restamos 105 de 252, obtenemos 147. El MCD de 105 y 147 sigue siendo 21. Al repetir este proceso, los números se hacen más pequeños hasta que son iguales. Ese número es el MCD original.
Una versión más rápida del algoritmo usa los restos de las divisiones en lugar de las restas. Esta versión es la que se usa más a menudo hoy en día. Con esta mejora, el algoritmo es muy eficiente y no necesita muchos pasos para encontrar el MCD.
Contenido
¿Qué es el Máximo Común Divisor (MCD)?
El Máximo Común Divisor (MCD) de dos números es el número más grande que los divide a ambos de forma exacta, sin dejar resto. Por ejemplo, si tenemos los números 12 y 18:
- Los divisores de 12 son: 1, 2, 3, 4, 6, 12.
- Los divisores de 18 son: 1, 2, 3, 6, 9, 18.
Los divisores comunes son 1, 2, 3 y 6. El más grande de ellos es 6. Así, el MCD de 12 y 18 es 6.
¿Cómo funciona el algoritmo de Euclides?
El algoritmo de Euclides se basa en una idea sencilla: el MCD de dos números no cambia si reemplazamos el número más grande por el resto de la división del número más grande entre el más pequeño. Repetimos este proceso hasta que el resto sea cero. El último resto que no fue cero es el MCD.
Pasos del algoritmo con un ejemplo
Vamos a calcular el MCD de 2366 y 273.
- Paso 1: Divide el número más grande (2366) entre el más pequeño (273).
* 2366 dividido entre 273 es 8, y el resto es 182. * Esto significa que el MCD de (2366, 273) es el mismo que el MCD de (273, 182).
- Paso 2: Ahora, divide el número anterior (273) entre el resto que obtuviste (182).
* 273 dividido entre 182 es 1, y el resto es 91. * Así, el MCD de (273, 182) es el mismo que el MCD de (182, 91).
- Paso 3: Repite el proceso: divide 182 entre 91.
* 182 dividido entre 91 es 2, y el resto es 0. * Cuando el resto es 0, el proceso termina. El MCD es el último número que usaste como divisor, que en este caso es 91.
Por lo tanto, el MCD de 2366 y 273 es 91.
| Paso | Operación | Significado |
|---|---|---|
| 1 | 2366 dividido entre 273 es 8 y sobran 182 |  |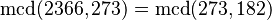
| 2 | 273 dividido entre 182 es 1 y sobran 91 |  |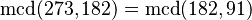
| 3 | 182 dividido entre 91 es 2 y sobra 0 |  |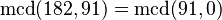
El MCD es 91.
¿Por qué funciona?
La clave es que el MCD de dos números (a, b) es igual al MCD del número más pequeño (b) y el resto de su división (r). Esto se repite hasta que el resto es cero. En ese momento, el divisor es el MCD.
El algoritmo de Euclides original (geométrico)
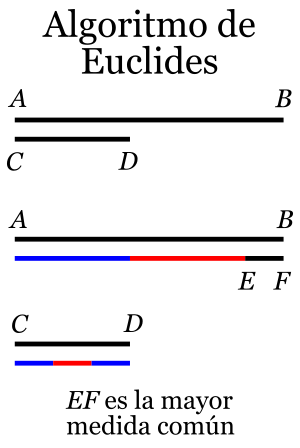
En la antigua Grecia, los matemáticos como Euclides veían los números como longitudes de segmentos. El algoritmo original se usaba para encontrar la "medida común más grande" de dos segmentos. Imagina que tienes dos varas de madera de diferentes longitudes. El algoritmo te ayudaría a encontrar la vara más larga que puedes usar para medir ambas varas exactamente, sin que sobre ni falte nada.
Euclides describió este método como un proceso de "restar continuamente" el segmento más corto del más largo. Si quedaba un resto, ese resto se convertía en el nuevo segmento más corto, y el proceso se repetía. El último segmento que medía exactamente al anterior era la "mayor medida común".
Aplicaciones del algoritmo de Euclides
El algoritmo de Euclides tiene muchas aplicaciones prácticas:
Simplificar fracciones
Una de las aplicaciones más comunes es simplificar fracciones a su forma más simple. Para simplificar una fracción como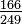 
, primero encuentras el MCD del numerador (166) y el denominador (249).
- Usando el algoritmo de Euclides, encontramos que el MCD de 166 y 249 es 83.
- Luego, divides tanto el numerador como el denominador por el MCD:
* 166 dividido por 83 es 2. * 249 dividido por 83 es 3.
- Así, la fracción simplificada es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle\frac 2 3 .
Fracciones continuas
El algoritmo también se usa para expresar una fracción como una fracción continua. Una fracción continua es una forma especial de escribir un número como una suma de un número entero y una fracción, donde el denominador de esa fracción es también una suma de un entero y una fracción, y así sucesivamente.
Por ejemplo, para la fracción Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle\frac{93164}{5826} , los cocientes que obtenemos en cada paso del algoritmo de Euclides (15, 1, 111, 26) se usan para construir la fracción continua: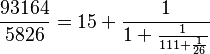 
Seguridad en Internet
Aunque parezca sorprendente, el algoritmo de Euclides es fundamental en la criptografía, que es la base de la seguridad en Internet. Ayuda a proteger nuestras comunicaciones, como cuando enviamos mensajes o hacemos compras en línea. Se utiliza en protocolos que aseguran que la información que enviamos sea privada y segura.
El algoritmo de Euclides extendido
El algoritmo de Euclides extendido no solo encuentra el MCD de dos números, sino que también encuentra otros dos números enteros, digamos 's' y 't', de tal manera que el MCD se puede escribir como una combinación de los números originales. Es decir, MCD(a, b) = a * s + b * t. Esto es muy útil en matemáticas avanzadas y en criptografía.
Por ejemplo, para los números 2366 y 273, sabemos que su MCD es 91. El algoritmo extendido nos permite encontrar que 91 se puede expresar como: 91 = 2366 * (-1) + 273 * (9) Aquí, 's' sería -1 y 't' sería 9.
¿Qué tan rápido es el algoritmo?
El algoritmo de Euclides es muy eficiente. Un matemático llamado Gabriel Lamé demostró en 1844 que el número de pasos que necesita el algoritmo para encontrar el MCD nunca es más de cinco veces el número de dígitos del número más pequeño. Esto significa que es muy rápido, incluso para números muy grandes.
Por ejemplo, para encontrar el MCD de 89 y 55 (que son números de la sucesión de Fibonacci, conocidos por ser un "caso difícil" para el algoritmo), solo se necesitan 9 pasos de división.
| Paso | Operación | Significado |
|---|---|---|
| 1 | 89 dividido entre 55 es 1 y sobran 34 |  |
| 2 | 55 dividido entre 34 es 1 y sobran 21 |  |
| 3 | 34 dividido entre 21 es 1 y sobran 13 |  |
| 4 | 21 dividido entre 13 es 1 y sobran 8 |  |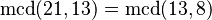
| 5 | 13 dividido entre 8 es 1 y sobran 5 |  |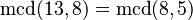
| 6 | 8 dividido entre 5 es 1 y sobran 3 |  |
| 7 | 5 dividido entre 3 es 1 y sobran 2 |  |
| 8 | 3 dividido entre 2 es 1 y sobran 1 |  |
| 9 | 2 dividido entre 1 es 2 y sobra 0 |  |
Galería de imágenes
-
AB y CD los segmentos conmensurables.
-
Véase también
En inglés: Euclidean algorithm Facts for Kids
