Hipótesis de Riemann para niños
La Hipótesis de Riemann, propuesta por el matemático Bernhard Riemann en 1859, es una de las conjeturas más famosas y difíciles de las matemáticas. Una conjetura es una idea o afirmación que parece ser cierta, pero que aún no ha sido demostrada con una prueba matemática rigurosa.
Esta hipótesis trata sobre los "ceros" de una función matemática muy especial llamada la función zeta de Riemann. Los "ceros" de una función son los valores donde la función da como resultado cero.
La Hipótesis de Riemann es muy importante porque está conectada con la forma en que se distribuyen los números primos (números que solo se pueden dividir por 1 y por sí mismos, como 2, 3, 5, 7, etc.). Resolverla ayudaría a entender mejor cómo aparecen los números primos en la secuencia de los números naturales.
Debido a su gran importancia, el Clay Mathematics Institute ha ofrecido un premio de un millón de dólares a la primera persona que logre demostrar que esta conjetura es verdadera. También es uno de los "Problemas del Milenio", una lista de siete grandes desafíos matemáticos sin resolver.
Contenido
¿Qué es la función zeta de Riemann?
La función zeta de Riemann, escrita como ζ(s), es una función matemática que se define para ciertos números. Al principio, se define como una suma infinita:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \zeta(s) = \frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots
Esta suma funciona bien para números donde la parte real de s es mayor que 1.
Un matemático llamado Leonhard Euler descubrió que esta misma función también se puede escribir como un producto infinito que usa solo números primos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \zeta(s) = \frac{1}{1-2^{-s}}\cdot\frac{1}{1-3^{-s}}\cdot\frac{1}{1-5^{-s}}\cdot\frac{1}{1-7^{-s}} \cdots
Esta conexión entre la función zeta y los números primos es lo que la hace tan fascinante.
Los ceros de la función zeta
La Hipótesis de Riemann se centra en los valores de s para los cuales la función ζ(s) es igual a cero. Hay dos tipos de ceros:
- Ceros triviales: Son fáciles de encontrar. La función zeta es cero para todos los números pares negativos (como -2, -4, -6, etc.).
- Ceros no triviales: Estos son los más interesantes y misteriosos. Se encuentran en una región especial del plano complejo (un tipo de gráfico para números complejos).
La Hipótesis de Riemann afirma que:
|
Esto significa que todos los ceros no triviales deberían estar en una línea vertical imaginaria en el plano complejo, donde la parte real del número es siempre 1/2. Esta línea se conoce como la "línea crítica".
Historia de la hipótesis
Origen y primeros avances
Bernhard Riemann mencionó esta conjetura en 1859 en su trabajo sobre los números primos. Aunque no la demostró, sabía que los ceros no triviales de la función zeta estaban cerca de la línea 1/2.
En 1896, los matemáticos Jacques Hadamard y de la Vallée-Poussin demostraron por separado que ningún cero podía estar exactamente en la línea donde la parte real de s es 1. Esto fue un paso clave para probar el teorema de los números primos, que describe cómo se distribuyen los primos.
El desafío de Hilbert
En 1900, el famoso matemático David Hilbert incluyó la Hipótesis de Riemann en su lista de los 23 problemas más importantes sin resolver de las matemáticas. Se dice que cuando le preguntaron qué haría si se despertara después de 500 años, respondió que su primera pregunta sería si la Hipótesis de Riemann ya había sido probada.
Más descubrimientos
En 1914, Godfrey Harold Hardy demostró que hay un número infinito de ceros en la línea crítica (donde la parte real es 1/2). Sin embargo, esto no prueba que *todos* los ceros estén allí.
La mayoría de los matemáticos creen que la conjetura es correcta, pero aún no hay una prueba definitiva. Se han realizado muchos cálculos para encontrar ceros y todos han estado en la línea crítica, pero encontrar un contraejemplo (un cero fuera de esa línea) la refutaría por completo.
En 2018, el matemático Michael Atiyah presentó una supuesta prueba, pero resultó ser incorrecta.
La hipótesis de Riemann y los números primos
La Hipótesis de Riemann tiene una conexión muy profunda con los números primos. Los ceros de la función zeta pueden interpretarse como "frecuencias" que controlan cómo se distribuyen los números primos.
Si la Hipótesis de Riemann fuera cierta, nos daría una forma muy precisa de estimar cuántos números primos hay hasta un cierto número. Por ejemplo, Helge von Koch demostró en 1901 que la hipótesis de Riemann es equivalente a una mejora muy importante del teorema de los números primos.
También ayudaría a entender mejor las distancias entre números primos consecutivos. Por ejemplo, el matemático Cramér sugirió que la hipótesis de Riemann implica una fórmula para predecir la distancia entre un primo y el siguiente.
Búsqueda de ceros
Los matemáticos y las computadoras han buscado incansablemente ceros de la función zeta para ver si alguno se desvía de la línea crítica.
- En 2004, Xavier Gourdon verificó numéricamente los primeros diez billones de ceros no triviales, y todos estaban en la línea crítica.
- Hasta 2005, el proyecto ZetaGrid, que usaba la capacidad de muchas computadoras conectadas, verificó billones de ceros por día. Ninguno de ellos fue un contraejemplo.
Aunque estos cálculos no demuestran la hipótesis, sí aumentan la confianza en que es verdadera, ya que no se ha encontrado ningún cero que la contradiga.
Galería de imágenes
-
Función zeta de Riemann a lo largo de la línea crítica con Re(s) = 1/2. Los valores reales se muestran en el eje horizontal y los valores imaginarios en el eje vertical. Re(ζ(1/2 + it)), Im(ζ(1/2 + it)) se representa con t entre -30 y 30.
-
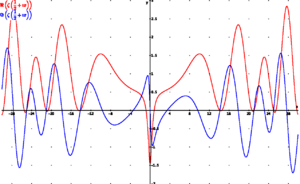
Parte real (rojo) y parte imaginaria (azul) de la función zeta de Riemann ζ(s) a lo largo de la recta crítica en el plano complejo con parte real Re(s) = 1/2. Los primeros no triviales ceros, donde ζ(s) es igual a cero, ocurren donde ambas curvas tocan el eje horizontal x, para números complejos con partes imaginarias Im(s) iguales a ±14,135, ±21,022 y ±25,011.
Véase también
En inglés: Riemann hypothesis Facts for Kids
