Número trascendente para niños
Un número trascendente es un tipo especial de número que no se puede obtener como la solución de una ecuación algebraica sencilla. Imagina que tienes una ecuación donde solo usas números enteros, como 2x + 3 = 0 o x² - 5 = 0. Los números trascendentes no son la respuesta a ninguna de estas ecuaciones.
Para entenderlo mejor, piensa en los números que ya conoces:
- Los números racionales son aquellos que se pueden escribir como una fracción (por ejemplo, 1/2, 3, -4/5). Estos son soluciones de ecuaciones muy simples, como 2x - 1 = 0 (donde x = 1/2).
- Los números irracionales son aquellos que no se pueden escribir como una fracción y tienen infinitos decimales sin un patrón que se repita (como la raíz cuadrada de 2). Algunos números irracionales son soluciones de ecuaciones algebraicas (por ejemplo, la raíz cuadrada de 2 es la solución de x² - 2 = 0). A estos se les llama números algebraicos.
Un número trascendente es un número real que no es algebraico. Esto significa que no es la solución de ninguna ecuación polinómica con coeficientes enteros. Los números trascendentes son un tipo de número irracional. Los ejemplos más famosos de números trascendentes son π (pi) y e.
Aunque hay muchísimos números trascendentes, es muy difícil demostrar que un número lo es. Por ejemplo, aún no se sabe si la constante de Euler (un número importante en matemáticas) es trascendente.
Contenido
¿Qué son los números trascendentes?
Los números trascendentes son aquellos que "van más allá" de lo que se puede expresar con ecuaciones algebraicas básicas. No pueden ser la raíz de un polinomio con coeficientes enteros. Esto los hace muy especiales en el mundo de las matemáticas.
¿Cómo se diferencian de otros números?
- Números racionales: Se pueden escribir como una fracción. Son soluciones de ecuaciones muy sencillas.
- Números algebraicos: Son soluciones de ecuaciones polinómicas con coeficientes enteros. Incluyen a los números racionales y a algunos irracionales (como la raíz cuadrada de 2).
- Números trascendentes: No son soluciones de ninguna ecuación polinómica con coeficientes enteros. Son un tipo de número irracional.
Historia de los números trascendentes
El concepto de "trascendente" fue mencionado por primera vez por el matemático Gottfried Leibniz en 1682. Él notó que algunas funciones no podían expresarse de forma algebraica. Más tarde, Euler definió los números trascendentes de una manera más moderna.
¿Quién demostró su existencia?
La existencia de los números trascendentes fue probada por primera vez en 1844 por Joseph Liouville. En 1851, Liouville mostró un ejemplo de un número trascendente, conocido como la "constante de Liouville". Este número tiene un patrón de unos y ceros muy particular: 0.110001000000000000000001000... donde los unos aparecen en las posiciones que son factoriales (1, 2, 6, 24, etc.).
¿Cuándo se demostró que pi y e son trascendentes?
El primer número del que se demostró que era trascendente sin haber sido creado específicamente para ello fue el número e. Esto lo hizo Charles Hermite en 1873. Poco después, en 1882, Carl Louis Ferdinand von Lindemann demostró que el número π también es trascendente.
¿Por qué es importante que pi sea trascendente?
El descubrimiento de que pi es trascendente resolvió un problema muy antiguo de la geometría griega: la cuadratura del círculo. Este problema consistía en construir un cuadrado con la misma área que un círculo dado, usando solo una regla y un compás. Como pi es trascendente, se demostró que es imposible resolver este problema de esa manera.
Ejemplos de números trascendentes
Aquí tienes algunos de los números trascendentes más conocidos:
- e (aproximadamente 2.71828)
- π (aproximadamente 3.14159)
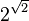(dos elevado a la raíz cuadrada de dos).- Los logaritmos naturales de números positivos que no son potencias de e.
- Los valores de las funciones trigonométricas (como seno o coseno) para la mayoría de los números algebraicos (excepto algunos casos especiales).
- El número de Champernowne: C10 = 0.123456789101112131415161718192021... (se forma escribiendo todos los números enteros seguidos).
- La constante de Liouville: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{k=1}^\infty 10^{-k!} = 0,110001000000000000000001000....
Galería de imágenes
-
Número π.
Véase también
En inglés: Transcendental number Facts for Kids
