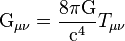Ecuaciones del campo de Einstein para niños
En el mundo de la física, las ecuaciones de campo de Einstein son un grupo de diez ecuaciones muy importantes. Fueron creadas por el famoso científico Albert Einstein como parte de su teoría de la relatividad general. Estas ecuaciones nos ayudan a entender cómo funciona la gravedad.
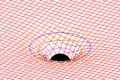
Según Einstein, la gravedad no es solo una fuerza que atrae las cosas, sino que es el resultado de que el espacio-tiempo (que es como el "tejido" del universo donde ocurren todos los eventos) se curva. ¿Y qué lo curva? Pues la materia y la energía que hay en él. Imagina que el espacio-tiempo es como una cama elástica: si pones una bola pesada en el centro, la cama se curva. Si luego lanzas una canica cerca, la canica rodará hacia la bola pesada, no porque la bola la "atraiga" directamente, sino porque la cama elástica está curvada. Así funciona la gravedad según Einstein.
Einstein publicó estas ecuaciones por primera vez en 1915. Básicamente, estas ecuaciones conectan la curvatura del espacio-tiempo en un lugar específico con la cantidad de energía y materia que hay en ese mismo lugar. Cuanta más materia haya, más se curvará el espacio-tiempo.
Cuando las cosas se mueven despacio (mucho más lento que la velocidad de la luz) y la gravedad no es muy fuerte, las ecuaciones de Einstein se parecen mucho a la ley de gravitación universal de Isaac Newton. Esto demuestra que la teoría de Einstein es una versión más completa y precisa de la gravedad.
Contenido
¿Cómo se escriben las Ecuaciones de Campo de Einstein?
Las ecuaciones de Einstein usan algo llamado "tensor métrico" para describir cómo es el espacio-tiempo en cuatro dimensiones (tres de espacio y una de tiempo). A partir de este tensor, se puede calcular la curvatura. La materia, por su parte, se describe con su "tensor de tensión-energía", que incluye la densidad y la presión de la materia.
La ecuación principal de Einstein nos dice cómo la materia curva el espacio-tiempo en cada punto. Se puede escribir así:
| Símbolo | Significado |
|---|---|
 |
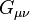Representa la curvatura del espacio-tiempo. |
 |
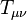Representa la cantidad de materia y energía. |
 |
Es la velocidad de la luz. |
 |
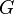Es la Constante de la gravitación universal, un número que indica la fuerza de la gravedad. |
Esta ecuación se cumple en cada punto del espacio-tiempo. Es la base matemática de la relatividad general.
¿Qué nos dice la ecuación de Einstein sobre el espacio?
La ecuación de Einstein nos muestra que la curvatura del espacio es proporcional a la densidad de la materia. Esto significa que, si hay mucha materia en un lugar, el espacio se curvará más.
Por ejemplo, si calculamos el "exceso radial" de la Tierra (la diferencia entre su radio real y lo que sería en un espacio plano), es de solo 1.5 milímetros. Para el Sol, que es mucho más grande, este exceso es de unos 495 metros. Esto nos da una idea de cómo la materia curva el espacio a su alrededor.
Lo asombroso de esta ecuación es que, aunque parece que solo hace pequeñas correcciones a la geometría que conocemos, de ella se pueden derivar muchas leyes importantes de la física. Por ejemplo, si imaginamos que la velocidad de la luz fuera infinita, las ecuaciones de Einstein nos llevarían a la ley de gravitación universal de Newton. También nos ayudan a entender cómo se conservan la masa y el movimiento.
Además, si consideramos que el espacio tiene cuatro dimensiones (las tres que vemos más una muy pequeña y enrollada), las ecuaciones de Einstein también nos permiten entender el electromagnetismo, incluyendo las ecuaciones de Maxwell y la ley de Coulomb sobre las cargas eléctricas.
El Límite Clásico: Conexión con Newton
Cuando hablamos del "límite clásico", nos referimos a situaciones donde la gravedad es débil y las velocidades son bajas, como las que experimentamos en nuestra vida diaria. En estas condiciones, las ecuaciones de Einstein se simplifican y se convierten en la ecuación de Poisson, que es la forma clásica de describir cómo el potencial gravitatorio se relaciona con la densidad de la materia. Esto demuestra que la teoría de Einstein es una extensión de la física de Newton, que funciona muy bien para la mayoría de las situaciones cotidianas.
Soluciones de las Ecuaciones de Campo de Einstein
Una "solución" de las ecuaciones de Einstein es una descripción de cómo se curva el espacio-tiempo para una distribución específica de masa y presión. Aquí te presentamos algunas soluciones importantes:
Masa Esférica y Estática
Cuando tenemos una masa que es perfectamente esférica y no se mueve (estática), como una estrella que no gira, la solución a las ecuaciones de Einstein se llama la métrica de Schwarzschild. Esta solución predice la existencia de un horizonte de sucesos, que es un punto sin retorno más allá del cual nada, ni siquiera la luz, puede escapar. Esto nos lleva a la idea de un agujero negro, un objeto tan denso que su gravedad es inmensa.
Masa en Rotación con Simetría Axial
Si la masa es esférica pero está girando, como una estrella que rota, la solución se llama la métrica de Kerr. Esta solución predice la posible existencia de un agujero negro en rotación. De estos agujeros negros se puede extraer energía de su rotación.
Universo Uniforme y en Expansión
Para describir el universo en su conjunto, que se considera bastante uniforme y homogéneo (igual en todas direcciones y en todos los lugares), la solución es la métrica de Robertson-Walker. Esta solución es fundamental para entender cómo evoluciona el universo y predice que nuestro universo está en expansión.
Galería de imágenes
-
Representación de la curvatura del espacio-tiempo causada por la materia, según las ecuaciones de Einstein.
-
Representación de la curvatura del espacio-tiempo cerca de un objeto muy denso, como un agujero negro.
Véase también
En inglés: Einstein field equations Facts for Kids
