OEIS para niños

Enciclopedia para niños

La Enciclopedia electrónica de secuencias de enteros (conocida como OEIS, por sus siglas en inglés de On-Line Encyclopedia of Integer Sequences) es una gran base de datos en línea. Su propósito es guardar y organizar listas de números enteros, llamadas secuencias.

Esta enciclopedia es muy útil para matemáticos profesionales, pero también es divertida para cualquiera que disfrute de los juegos y desafíos matemáticos.

Hasta enero de 2022, la OEIS tenía más de 350.000 secuencias. Esto la convierte en la base de datos más grande de su tipo. Algunas de las secuencias más famosas que puedes encontrar son:

La lista de números primos (A000040).
La sucesión de Fibonacci (A000045).
Y muchas otras sin un nombre especial, como los números que no son cuadrados (A028761).

Cada entrada en la OEIS incluye los primeros números de la secuencia, palabras clave que la describen, por qué es importante en matemáticas, fórmulas, enlaces a trabajos relacionados y mucho más. Puedes buscar secuencias usando cualquiera de estos datos, o incluso buscando partes de una secuencia.

Datos para niños Enciclopedia electrónica de secuencias de enteros


Información general
Dominio	https://OEIS.org
Tipo	Enciclopedia en línea Base de datos en línea
Licencia	CC BY-NC 3.0 Creative Commons Atribución/Reconocimiento-CompartirIgual 4.0 Internacional
Gestión
Desarrollador	Neil Sloane
Operador	OEIS Foundation
Lanzamiento	1996
Estadísticas

Historia de la OEIS

¿Quién creó la OEIS?

Neil Sloane comenzó a recopilar secuencias de números enteros en la década de 1960. Lo hacía para ayudar en su trabajo de combinatoria, una rama de las matemáticas. Al principio, guardaba su colección en tarjetas perforadas.

De libros a Internet

La colección de Sloane se publicó dos veces en forma de libro:

A Handbook of Integer Sequences (1973), con 2.400 secuencias.
The Encyclopedia of Integer Sequences (1995), con 5.487 secuencias.

Estos libros fueron muy populares. Después de la segunda publicación, muchos matemáticos empezaron a enviar nuevas secuencias a Sloane. La colección creció tanto que ya no era práctico tenerla en libros. Cuando llegó a 16.000 secuencias, Sloane decidió ponerla en Internet. Primero, como un servicio de correo electrónico en 1995, y luego como una página web en 1996.

Hoy en día, la base de datos sigue creciendo. Se añaden aproximadamente 10.000 nuevas entradas cada año. En 2004, Sloane celebró la secuencia número 100.000 (A100000). En 2006, la página web se actualizó para ser más fácil de usar y con mejores opciones de búsqueda.

Neil Sloane ha dirigido la base de datos por más de 40 años. Desde 2002, un grupo de editores y voluntarios le ayudan a mantenerla.

Tipos de secuencias en la OEIS

¿Solo números enteros?

Aunque se llama "Enciclopedia de secuencias de enteros", la OEIS también guarda secuencias de fracciones, números complejos y dígitos de números trascendentes. Para hacerlo, los representa como secuencias de números enteros.

Por ejemplo, las secuencias de números racionales (fracciones) se muestran con dos secuencias. Una es para los numeradores y otra para los denominadores. Un ejemplo es la quinta sucesión de Farey: 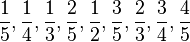${1 \over 5}, {1 \over 4}, {1 \over 3}, {2 \over 5}, {1 \over 2}, {3 \over 5}, {2 \over 3}, {3 \over 4}, {4 \over 5}$ . En la OEIS, se lista como la secuencia de numeradores: 1, 1, 1, 2, 1, 3, 2, 3, 4 (A006842). Y la secuencia de denominadores: 5, 4, 3, 5, 2, 5, 3, 4, 5 (A006843).

Algunos números irracionales importantes, como pi (π = 3.1415926535897…), aparecen como la lista infinita de sus decimales: 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, … (A000796).

Cómo se organizan las secuencias

Convenciones de la OEIS

La OEIS usa un formato de texto simple (ASCII) para mostrar la información. Por ejemplo, usa f(n) para funciones y n para la variable. Las letras griegas se escriben con su nombre completo, como mu para μ.

Cada secuencia tiene un identificador único: la letra A seguida de seis dígitos, como A000040.

Los números de una secuencia se separan con comas. Los dígitos de cada número se escriben juntos, sin comas ni espacios.

En los comentarios y fórmulas, a(n) significa el término número n de la secuencia a.

El significado especial del cero

A veces, el cero se usa para indicar que un elemento no existe en una secuencia. Por ejemplo, la secuencia A104157 busca el número primo más pequeño necesario para crear un cuadrado mágico de cierto tamaño. Si no existe tal cuadrado, se usa 0. Para un cuadrado de 2x2, no existe, así que a(2) es 0.

Orden lexicográfico

La OEIS organiza las secuencias en orden lexicográfico. Esto significa que las secuencias se ordenan como si fueran palabras en un diccionario. Para hacer esto, se ignoran los ceros y unos al principio, y también los signos de los números.

Por ejemplo, si tuviéramos estas secuencias:

Secuencia #1: 2, 3, 5, 7, 11, ... (números primos)
Secuencia #2: 2, 3, 5, 7, 11, 101, ... (primos palindrómicos)
Secuencia #3: 0, 1, 1, 2, 3, 5, 8, ... (sucesión de Fibonacci)
Secuencia #4: 1, 2, 4, 7, 11, ... (número máximo de trozos al cortar un círculo)
Secuencia #5: 1, -3, -8, -3, -24, ... (coeficientes de una serie)

En el orden lexicográfico de OEIS (ignorando ceros, unos y signos al principio), quedarían así:

#1 (2, 3, 5, ...)
#2 (2, 3, 5, ...)
#3 (0, 1, 1, 2, ...)
#4 (1, 2, 4, ...)
#5 (1, -3, -8, ...)

Pero si no se normalizan, el orden sería: #3, #5, #4, #1, #2.

Autoreferencias

Al principio, Sloane no quería incluir secuencias que se basaran en el orden de las propias secuencias de la OEIS. Pero luego aceptó algunas.

Una de las primeras fue A031135 (luego A091967), que es "a(n) = término número n de la secuencia An". Esto significa que el primer término de A091967 es el primer término de A000001, el segundo es el segundo de A000002, y así sucesivamente.

Ejemplo de una entrada de OEIS

Aquí puedes ver una parte de la entrada A046970, que tiene mucha información:

ID Number: A046970
URL:       http://www.research.att.com/projects/OEIS?Anum=A046970
Sequence:  1,3,8,3,24,24,48,3,8,72,120,24,168,144,192,3,288,24,360,72,
           384,360,528,24,24,504,8,144,840,576,960,3,960,864,1152,24,
           1368,1080,1344,72,1680,1152,1848,360,192,1584,2208,24,48,72,
           2304,504,2808,24,2880,144,2880,2520,3480,576
Signed:    1,-3,-8,-3,-24,24,-48,-3,-8,72,-120,24,-168,144,192,-3,-288,
           24,-360,72,384,360,-528,24,-24,504,-8,144,-840,-576,-960,-3,
           960,864,1152,24,-1368,1080,1344,72,-1680,-1152,-1848,360,
           192,1584,-2208,24,-48,72,2304,504,-2808,24,2880,144,2880,
           2520,-3480,-576
Name:      Generated from Riemann Zeta function: coefficients in series
              expansion of Zeta(n+2)/Zeta(n).
Comments:  ...
           Apart from signs also Sum_{d|n} core(d)^2*mu(n/d) where core(x) is
              the squarefree part of x. - Benoit Cloitre
              (abcloitre(AT)modulonet.fr), May 31 2002
References M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions,
              Dover Publications, 1965, pp. 805-811.
Links:     Wikipedia, Riemann zeta function.
Formula:   Multiplicative with a(p^e) = 1-p^2. a(n) = Sum_{d|n} mu(d)*d^2.
Example:   a(3) = -8 because the divisors of 3 are {1, 3}, and mu(1)*1^2 + mu(3)*3^2 =
              -8.
           a(4) = -3 because the divisors of 4 are {1, 2, 4}, and mu(1)*1^2 +
              mu(2)*2^2 + mu(4)*4^2 = -3
Math'ca:   muDD[d_] := MoebiusMu[d]*d^2; Table[Plus @@ muDD[Divisors[n]], {n,
              60}] (Lopez)
Program:   (PARI) A046970(n)=sumdiv(n,d,d^2*moebius(d)) (Benoit Cloitre)
See also:  Sequence in context: A016623 A046543 A035292 this_sequence A058936
              A002017 A086179
           Adjacent sequences: A046967 A046968 A046969 this_sequence A046971
              A046972 A046973
           Cf. A027641 and A027642.
Keywords:  sign,mult
Offset:    1
Author(s): Douglas Stoll, dougstoll(AT)email.msn.com
Extension: Corrected and extended by Vladeta Jovovic (vladeta(AT)Eunet.yu),
              Jul 25 2001
           ...

Campos de información en cada entrada

ID (identificador)

Cada secuencia tiene un número de serie: una letra A seguida de seis dígitos. Estos números los asigna un editor o un sistema automático. Un número más alto generalmente significa que la secuencia se añadió más tarde.

URL

Este campo muestra la dirección web para acceder directamente a la página de la secuencia.

Secuencia

Aquí se listan los números de la secuencia. Si la secuencia es finita (tiene un número limitado de términos), puede que no se muestren todos. Para saber si hay más números, se revisan las palabras clave "full", "fini" o "more".

Con signo

Si una secuencia tiene números negativos, este campo muestra los términos con sus signos correctos. El campo "Sequence" principal solo muestra los valores positivos.

Nombre

Es el nombre de la secuencia o una descripción corta. A menudo incluye la fórmula si es sencilla. Por ejemplo, A000578 se llama "Los cubos: a(n) = n^3".

Comentarios

Aquí se añade información adicional sobre la secuencia que no encaja en otros campos. A menudo se explican relaciones curiosas con otras secuencias o aplicaciones interesantes.

Programas (Maple, Mathematica, etc.)

Se incluyen programas de ordenador (como Maple o Mathematica) que se pueden usar para calcular los términos de la secuencia.

"Véase también"

Este campo muestra enlaces a otras secuencias relacionadas. Incluye secuencias cercanas en el orden lexicográfico y por número de ID.

Palabras clave

La OEIS usa palabras clave cortas (de 4 o 5 letras) para describir características de cada secuencia. Algunas de ellas son:

base: La secuencia depende de la base numérica usada (por ejemplo, si es binario o decimal).
brev: La secuencia es muy corta y no muy útil para analizar.
cofr: La secuencia representa una fracción continua.
cons: La secuencia son los dígitos de una constante matemática importante, como π.
core: Es una secuencia fundamental por su importancia en matemáticas.
dead: Secuencias que tienen errores o son duplicados.
dumb: Una palabra subjetiva para secuencias poco importantes o sin relación directa con las matemáticas.
dupe: Para marcar secuencias repetidas.
eigen: Secuencia de autovalores.
easy: Los términos de la secuencia son fáciles de calcular.
fini: La secuencia es finita (tiene un número limitado de términos).
frac: Secuencia de numeradores o denominadores de una fracción.
full: El campo "Sequence" muestra la secuencia completa.
hard: Los términos de la secuencia son muy difíciles de calcular.
more: No se conocen los siguientes términos de la secuencia.
mult: La secuencia corresponde a una función multiplicativa.
new: Se añadió en las últimas dos semanas o ha recibido atención reciente.
nice: Una palabra subjetiva para secuencias excepcionalmente interesantes.
nonn: La secuencia solo contiene números no negativos (puede incluir ceros).
obsc: La secuencia no es clara y necesita una mejor definición.
sign: Algunos o todos los valores de la secuencia son negativos.
tabl: Una tabla de números que se lee fila por fila para formar la secuencia.
unkn: Se sabe poco sobre esta secuencia, ni siquiera la fórmula que la produce.
walk: La secuencia cuenta el número de caminos en un espacio.
word: La secuencia depende de las palabras de un idioma específico.

Algunas palabras clave no pueden ir juntas, como "easy" y "hard".

Desplazamiento

El desplazamiento (offset) es el índice del primer término de la secuencia. Indica con qué número n empieza la fórmula a(n). Suele ser 0 o 1.

Por ejemplo, si la secuencia de cuadrados es 0, 1, 4, 9, ..., el desplazamiento es 0. Si es 1, 4, 9, ..., el desplazamiento es 1.

Autor

Aquí se indica la persona que envió la secuencia, incluso si es muy conocida. Se incluye el nombre y el correo electrónico. Si el autor es Neil Sloane, aparece como "njas".

Búsquedas en OEIS

La OEIS permite buscar secuencias de varias maneras. Puedes buscar por los números de la secuencia, por palabras clave, por el nombre de la secuencia o por su identificador (el número A).

Algunos ejemplos de búsqueda son:

1,4,9,16,25,36,64 (busca secuencias que contengan estos números)
"fermat's little theorem" (busca por nombre o descripción)
author:Guy keyword:nice (busca secuencias de un autor específico con una palabra clave)
id:A64413 o simplemente A64413 (busca por el número de identificación de la secuencia)

Errores y problemas en OEIS

A pesar de su gran tamaño, la OEIS tiene muy pocos errores. Esto se debe a que la mayoría de las secuencias incluyen una fórmula o un programa de ordenador, y muchas personas revisan y amplían los resultados.

Los errores más comunes no están en los números de la secuencia, sino en otros campos:

Palabras clave que faltan: Algunas secuencias no tienen todas las palabras clave que deberían.
Desplazamiento incorrecto: A veces, el punto de inicio de la secuencia (el offset) no es el correcto.
Duplicados: Hay secuencias que son iguales (tienen los mismos números y fórmula), aunque el nombre sea diferente. Cuando esto ocurre, se etiquetan con la palabra clave "dupe".

Véase también

En inglés: On-Line Encyclopedia of Integer Sequences Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=OEIS&oldid=4900066»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

OEIS para Niños. Enciclopedia Kiddle.