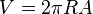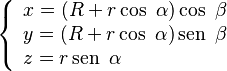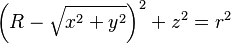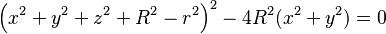Toroide para niños
Un toroide es una forma geométrica especial que se crea al girar una figura plana y cerrada (como un círculo o un cuadrado) alrededor de una línea recta. Imagina que tienes una forma de papel y la haces girar muy rápido alrededor de un palo; la forma que se dibuja en el aire es un toroide.
Las formas de toroide son muy comunes en la vida diaria. Por ejemplo, la superficie de una rosquilla, un anillo o un flotador de piscina tienen forma de toroide. La palabra "toroide" también se usa para describir un tipo de figura tridimensional que se forma de manera similar.
Cuando la figura que gira es un círculo perfecto, la forma que se crea se llama toro. Es importante recordar que un toroide es la superficie (como la piel de una fruta), no el objeto sólido completo. Por ejemplo, un anillo es un objeto sólido, pero su superficie exterior tiene forma de toro.
Contenido
¿Cómo se forma un toroide?
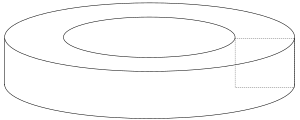
Un toroide se forma cuando una figura plana y cerrada, como un polígono (un cuadrado, un triángulo) o una curva (un círculo), gira alrededor de una línea recta que no la toca. Esta línea se llama el eje de rotación.
El toro: un tipo especial de toroide
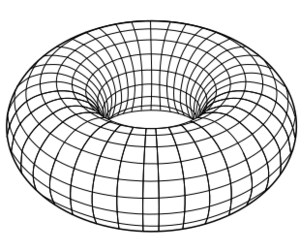
El toro es el tipo de toroide más conocido. Se forma cuando la figura que gira es una circunferencia. Piensa en un flotador de piscina o una rosquilla: su superficie es un toro.
¿Cómo se calcula el volumen de un toroide?
El volumen es la cantidad de espacio que ocupa un objeto. Para calcular el volumen de un toroide, se usa una fórmula que depende de dos cosas:
- La distancia desde el centro de la figura que gira hasta el eje de rotación (llamada R).
- El área de la figura plana que gira (llamada A).
La fórmula es:
Donde V es el volumen, π (pi) es un número constante (aproximadamente 3.14159), R es la distancia al eje de rotación y A es el área de la figura que gira.
¿Cómo se describen los toroides con matemáticas?
Para describir la superficie de un toroide de forma precisa, los matemáticos usan ecuaciones. Estas ecuaciones nos permiten saber la posición exacta de cualquier punto en la superficie del toroide.
Ecuaciones paramétricas
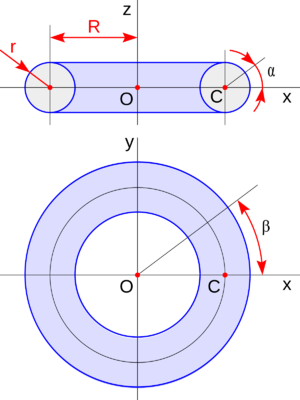
Imagina que quieres encontrar un punto específico en la superficie de un toro. Puedes usar dos ángulos, llamados α (alfa) y β (beta), como si fueran coordenadas en un mapa. Estos ángulos te dicen dónde está el punto en la superficie.
Las ecuaciones paramétricas para un toro son:
Aquí, R es la distancia del centro del toro al eje de giro, y r es el radio del círculo que gira para formar el toro. Las letras x, y, z son las coordenadas del punto en el espacio.
Ecuación cartesiana
También se puede describir un toro con una sola ecuación que relaciona las coordenadas x, y y z de cualquier punto en su superficie. Esta ecuación es un poco más compleja, pero nos da la misma información.
La ecuación cartesiana de un toro cuyo eje de giro es el eje z es:
Esta ecuación se puede reescribir de una forma más desarrollada:
Cualquier punto (x, y, z) que cumpla esta ecuación está en la superficie del toro.
Galería de imágenes
Véase también
 En inglés: Toroid Facts for Kids
En inglés: Toroid Facts for Kids
- Toro (geometría)
- Anexo:Ecuaciones de figuras geométricas