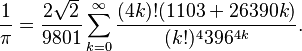Srinivasa Ramanujan para niños

Datos para niños Srinivasa Ramanujan
Srinivasa Aiyangar Ramanujan
Información personal
Nacimiento	22 de diciembre de 1887 Erode, Tamil Nadu, Raj Británico
Fallecimiento	26 de abril de 1920 (32 años) Kumbakonam, Tamil Nadu, Raj Británico
Causa de muerte	Amebiasis
Residencia	Raj Británico (actual India) Reino Unido
Nacionalidad	indio
Religión	Hindú
Familia
Cónyuge	Janakiammal
Educación
Educado en	Universidad de Cambridge
Supervisores doctorales	G. H. Hardy J. E. Littlewood
Supervisor doctoral	Godfrey Harold Hardy y John Edensor Littlewood
Alumno de	John Edensor Littlewood
Información profesional
Área	Matemáticas
Conocido por	Suma de Ramanujan Constante de Landau-Ramanujan Constante de Ramanujan-Soldner Identidades de Rogers-Ramanujan
Empleador	Puerto de Chennai (1912-1914) Trinity College (1916-1919)
Obras notables	constante de Landau-Ramanujan Función theta de Ramanujan identidades de Rogers-Ramanujan constante de Ramanujan-Soldner Número de Hardy-Ramanujan Suma de Ramanujan Ecuación de Ramanujan–Nagell número primo de Ramanujan Conjetura de Ramanujan–Petersson sumatorio de Ramanujan grafo de Ramanujan Fracción continua de Rogers-Ramanujan Series de Ramanujan-Sato función tau de Ramanujan Forma cuadrática ternaria de Ramanujan
Miembro de	Royal Society de Londres
Distinciones	Fellow of Trinity College (1918) Miembro de la Royal Society (1918)
Firma

Srinivāsa Aiyangār Rāmānujan ( en tamil, ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன், transliterado: Srinivasa Ramanujan Iyengar o simplemente como Ramanujan; Erode, Tamil Nadu, 22 de diciembre de 1887- Kumbakonam, Tamil Nadu, 26 de abril de 1920) fue un matemático autodidacta indio que, con una mínima educación académica en matemáticas puras, hizo contribuciones extraordinarias al análisis matemático, la teoría de números, las series y las fracciones continuas. Ramanujan desarrolló inicialmente su propia investigación matemática en forma aislada, que fue rápidamente reconocida por los matemáticos indios. Cuando sus habilidades se hicieron evidentes para una comunidad matemática más amplia, centrada en Europa en ese momento, comenzó su famosa colaboración con el matemático británico G. H. Hardy. Redescubrió teoremas conocidos previamente, además de formular numerosas nuevas proposiciones.

Durante su corta vida, Ramanujan fue capaz de compilar casi 3900 resultados independientes (en su mayoría identidades y ecuaciones). Casi todos sus hallazgos se han demostrado válidos, aunque algunos ya eran previamente conocidos. Logró resultados que eran a la vez originales y muy poco convencionales, como los números primos de Ramanujan y la función theta de Ramanujan, que a su vez han inspirado una gran cantidad de investigaciones posteriores.

Datos biográficos

Primeros años

Casa de Ramanujan. Sarangapani Street, Kumbakonam

Ramanujan nació el 22 de diciembre de 1887 en Erode, en la provincia de Madrás, por entonces perteneciente al Imperio Británico, en la residencia de sus abuelos maternos. Descendiente de una familia de brahmanes, su padre, K. Srinivasa Iyengar, trabajaba como empleado en una tienda de saris y provenía del barrio de Thanjavur. Su madre, Komalatammal, era un ama de casa, aficionada a cantar en un templo local. Vivían en una casa tradicional de la calle Sarangapani de la ciudad de Kumbakonam (la casa de la familia es actualmente un museo). Cuando Ramanujan tenía un año y medio de edad, su madre dio a luz a otro hijo llamado Sadagopan, que murió menos de tres meses después. En diciembre de 1889, Ramanujan padeció la viruela, de la que pudo recuperarse a diferencia de los miles de personas en el distrito de Thanjavur que murieron de la enfermedad aquel año. Se trasladó con su madre a la casa de sus abuelos maternos en Kanchipuram, cerca de Madrás (ahora Chennai). En noviembre de 1891, y nuevamente en 1894, su madre dio a luz a otros dos hijos, que murieron en la infancia.

El 1 de octubre de 1892, Ramanujan se matriculó en la escuela local. En marzo de 1894 fue trasladado a una escuela de grado medio. Después de que su abuelo materno perdiera su trabajo como oficial de la corte en Kanchipuram, Ramanujan y su madre regresaron a Kumbakonam y fue inscrito en la escuela primaria de Kangayan. Cuando su abuelo paterno murió, fue enviado de vuelta con sus abuelos maternos, quienes entonces vivían en Madrás. La escuela en Madrás no le gustaba, y el joven Ramanujan evitaba acudir a clase siempre que podía. Su familia contrató a un agente de policía local para asegurarse de que asistía a la escuela. Seis meses después, Ramanujan estaba de vuelta en Kumbakonam.

Dado que el padre de Ramanujan se pasaba en su trabajo la mayor parte del día, fue su madre quien cuidó de él casi en exclusiva cuando era niño. La relación entre ambos fue muy estrecha. Ella fue la que le instruyó en la tradición y en las puranas (literatura tradicional hinduista). Aprendió a cantar canciones religiosas, para asistir a las pujas en el templo, y a mantener determinados hábitos alimentarios propios de la cultura de los brahmanes. Ramanujan comenzó por fin a rendir satisfactoriamente en la escuela primaria de Kangayan. Justo antes de cumplir diez años, en noviembre de 1897, pasó sus exámenes de primaria en inglés, idioma tamil, geografía y aritmética, con las mejores calificaciones del distrito. Ese año, Ramanujan entró en la escuela secundaria superior de la ciudad, donde se encontró con las matemáticas formales por primera vez.

Con once años, Ramanujan había agotado el conocimiento matemático de dos estudiantes universitarios que eran inquilinos en su casa. Fue más tarde cuando le prestaron un libro de trigonometría avanzada escrito por S. L. Loney. Llegó a dominar por completo este libro con trece años y descubrió teoremas sofisticados por su cuenta. A los catorce años, estaba recibiendo certificados de mérito y premios académicos que continuaron durante toda su carrera escolar y también ayudaba a la dirección de la escuela colaborando en la logística de la asignación de sus 1200 estudiantes (cada uno con sus propias necesidades) a sus poco más de 35 profesores. Completaba los exámenes matemáticos en la mitad del tiempo asignado, y mostró una sorprendente familiaridad con la geometría y con las series infinitas. Ramanujan fue instruido en cómo resolver ecuaciones cúbicas en 1902 y a continuación encontró su propio método para resolver las de cuarto grado. Al año siguiente, sin saber que la ecuación de quinto grado no podía ser resuelta por radicales como había demostrado Évariste Galois setenta años antes, trató de resolverla por su cuenta.

En 1903, cuando tenía 16 años, Ramanujan obtuvo de un amigo una copia de un libro de G. S. Carr prestado en una biblioteca. El libro, titulado Synopsis of Pure Mathematics, era una colección de 5000 teoremas. Ramanujan estudió los artículos y el contenido del libro en detalle. Este libro es generalmente reconocido como un elemento clave para despertar el genio de Ramanujan. Al año siguiente, había trabajado de manera independiente e investigó los números de Bernoulli y había calculado la constante de Euler–Mascheroni con 15 decimales de precisión. Sus compañeros de aquella época comentaron después que "rara vez lo entendían" y que sentían por él "un temor respetuoso".

Cuando se graduó en la escuela secundaria en 1904, Ramanujan fue galardonado con el premio de matemáticas K. Ranganatha Rao por el director de la escuela, Krishnaswami Iyer. Iyer distinguió a Ramanujan como un estudiante sobresaliente que merecía una puntuación más alta que la máxima nota posible. Recibió una beca para estudiar en el Government Arts College de Kumbakonam. Sin embargo, Ramanujan estaba tan concentrado en el estudio de las matemáticas que no era capaz de dedicarse a otros asuntos, hasta el punto de que perdió la beca en el proceso de su tramitación. En agosto de 1905, se escapó de su casa en dirección a Visakhapatnam y se quedó en Rajahmundry alrededor de un mes. Más tarde se matriculó en el Pachaiyappa's College de Madrás. Nuevamente destacó en matemáticas, pero tuvo problemas con otras materias como la fisiología. Ramanujan falló en su examen de Fellow of Arts en diciembre de 1906 y de nuevo un año más tarde. Sin un título, dejó la universidad y continuó con la investigación independiente en matemáticas. En este punto de su vida, subsistió en la pobreza extrema y estuvo a menudo al borde de la inanición.

Edad adulta en la India

El 14 de julio de 1909, Ramanujan se casó con una novia de diez años de edad, Srimathi Janaki (Janakiammal) (21 de marzo de 1899 - 13 de abril de 1994) procedente de Rajendram, un pueblo cercano a la estación de ferrocarril de Marudur (distrito de Karur). El padre de Ramanujan no participó en la ceremonia del matrimonio.

Después de la unión, Ramanujan desarrolló un hidrocele testis, que pudo haber sido tratada con una operación quirúrgica de rutina, pero su familia carecía del dinero necesario para costear la operación. No fue hasta enero de 1910, cuando un médico se ofreció a hacer la cirugía gratuitamente.

Después de su cirugía exitosa, Ramanujan buscó un empleo. Se quedó en casa de sus amigos mientras iba de puerta en puerta en torno a la ciudad de Madrás (actualmente Chennai) en busca de un trabajo de oficina. Para conseguir algo de dinero, fue tutor de algunos estudiantes de la Universidad de la Presidencia que se preparaban para su examen de First Arts.

A finales de 1910, Ramanujan estaba enfermo de nuevo, posiblemente como resultado de la cirugía que se le practicó a principios de año. Temía por su salud, e incluso le llegó a encargar a su amigo, R. Radakrishna Iyer, que "se entregasen [los cuadernos matemáticos de Ramanujan] al profesor Singaravelu Mudaliar [profesor de matemáticas en el Colegio de Pachaiyappa] o al profesor británico Edward B. Ross, del Madras Christian College". Después de que Ramanujan sanó de nuevo, recuperó sus cuadernos de Iyer y tomó un tren hacia el norte desde Kumbakonam a Viluppuram, una ciudad costera por entonces bajo control francés.

Atención hacia las matemáticas

Ramanujan conoció al alto funcionario V. Ramaswamy Aiyer, que había fundado recientemente la Sociedad Matemática de la India. Deseando conseguir un trabajo en el departamento de recaudación, donde Ramaswamy Aiyer trabajaba, le mostró sus cuadernos de matemáticas. Como Ramaswamy Aiyer recordó más tarde:

Me llamaron la atención los extraordinarios resultados matemáticos contenidos en ellos [los cuadernos]. Yo no tenía en mente ahogar su genio con un puesto en los peldaños más bajos del departamento de recaudación.

Ramaswamy Aiyer envió cartas de presentación de Ramanujan a sus amigos matemáticos en Madrás. Algunos de estos amigos vieron su trabajo y le dieron a su vez cartas de presentación para R. Ramachandra Rao, recaudador del distrito de Nellore y secretario de la Sociedad Matemática de la India. Ramachandra Rao quedó impresionado por la investigación de Ramanujan, pero dudaba de que en realidad fuera su propia obra. Ramanujan menciona una correspondencia que tuvo con el profesor Saldhana, un matemático notable de Bombay, en la que Saldhana expresaba una falta de comprensión de su obra, pero llegaba a la conclusión de que Ramanujan no era un farsante. Su amigo C.V. Rajagopalachari persistió ante Ramachandra Rao y trató de sofocar cualquier duda sobre la integridad académica de Ramanujan. Rao accedió a darle otra oportunidad, y escuchó a Ramanujan disertando sobre integrales elípticas, series hipergeométricas y su teoría de series divergentes. Rao manifestó en última instancia que se había "convertido", y que estaba convencido de la brillantez de la matemática de Ramanujan. Cuando Rao le preguntó lo que quería, Ramanujan respondió que necesitaba un poco de trabajo y apoyo financiero. Rao estuvo de acuerdo y lo envió a Madrás. Continuó su investigación matemática con la ayuda financiera de Rao cuidando de sus necesidades diarias. Ramanujan, con la ayuda de Ramaswamy Aiyer, pudo publicar su trabajo en el Diario de la Sociedad Matemática de la India.

Uno de los primeros problemas planteados en la revista fue:

Esperó a que llegase una solución durante tres ediciones de la revista, más de seis meses, pero no recibió ninguna. Al final, Ramanujan facilitó la solución al problema. En la página 105 de su primer cuaderno, formuló una ecuación que se podía utilizar para resolver el problema de la sucesión infinita de radicales anidados:

Utilizando esta ecuación, la respuesta a la pregunta planteada en el Diario era simplemente 3.

Ramanujan escribió su primer documento formal para el Diario sobre las propiedades de los números de Bernoulli. Una propiedad que descubrió fue que los denominadores (sucesión A027642 en OEIS) de las fracciones de números de Bernoulli eran siempre divisibles por seis. También ideó un método de cálculo B_n sobre la base de los números de Bernoulli anteriores. Uno de estos métodos era el siguiente:

Se observa que si n es par pero distinto de cero, entonces
(i) B_n es una fracción de Bernoulli y el numerador de en sus términos más bajos es un número primo,
(ii) el denominador de B_n contiene cada uno de los factores 2 y 3 una vez y solo una vez,
(iii) es un entero y consecuentemente es un 'entero impar'.

En su documento de 17 páginas, "Algunas propiedades de los números de Bernoulli", Ramanujan formuló tres pruebas, dos corolarios y tres conjeturas. Ramanujan al principio redactaba sus artículos con bastantes carencias. Como el editor del 'Diario' M. T. Narayana Iyengar señaló:

Los métodos del señor Ramanujan eran tan escuetos y los textos y su presentación tan faltos de claridad y precisión, que de ordinario [un lector de matemática], poco acostumbrado a este tipo de gimnasia intelectual, apenas podía seguirle.

Ramanujan escribió más tarde otro artículo y también siguió publicando problemas en el Diario. A principios de 1912, consiguió un trabajo temporal en la oficina de Contabilidad General de Madrás, con un salario de 20 rupias al mes. Duró allí solo unas semanas, solicitando entonces un puesto a las órdenes del Jefe de Contabilidad del Trust del Puerto de Madrás. En una carta de fecha 9 de febrero de 1912, Ramanujan escribió:

Sir,
Entiendo que hay una pasantía vacante en su oficina, y le ruego que considere mi solicitud. Tengo aprobado el examen de ingreso y los estudios del First Arts, pero no he podido proseguir mis estudios debido a varias circunstancias adversas. He estado, sin embargo, dedicando todo mi tiempo a las matemáticas y a su desarrollo. Puedo decir que estoy bastante seguro de que puedo hacer justicia a mi trabajo si soy nombrado para el puesto. Me permito confiar en que va a ser lo suficientemente bondadoso como para conferirme el nombramiento.

Se adjunta a su solicitud una recomendación de E. W. Middlemast, profesor de matemáticas en el Colegio Presidencial de Chennai, quien escribió que Ramanujan era "un joven de capacidad excepcional en Matemáticas". Tres semanas después de haber mandado la carta, el 1 de marzo, se enteró de que había sido aceptado como auxiliar de contabilidad, con un sueldo de 30 rupias al mes. En su oficina, Ramanujan completaba su trabajo fácil y rápidamente, por lo que podía pasar el tiempo restante haciendo investigación matemática. El jefe de Ramanujan, Sir Francis Spring, y S. Narayana Iyer, su colega que también era el tesorero de la Sociedad Matemática de la India, animaron a Ramanujan en sus actividades matemáticas.

Contacto con matemáticos británicos

En la primavera de 1913, Narayana Iyer, Ramachandra Rao y E. W. Middlemast trataron de presentar el trabajo de Ramanujan a los matemáticos británicos. Un matemático, M. J. M. Hill del University College de Londres, comentó que los trabajos de Ramanujan "estaban llenos de agujeros", señalando que aunque Ramanujan tenía "un cierto gusto por las matemáticas, y un poco de habilidad", carecía de la formación académica y de los fundamentos necesarios para ser aceptado por la comunidad matemática. Aunque Hill no se ofreció a tomar a Ramanujan como estudiante, sí le dio asesoramiento profesional completo y formal en su trabajo. Con la ayuda de amigos, Ramanujan redactó cartas dirigidas a los principales matemáticos de la Universidad de Cambridge.

Los dos primeros profesores, H. F. Baker y E. W. Hobson, devolvieron los escritos de Ramanujan sin comentarios. El 16 de enero de 1913, Ramanujan escribió a G. H. Hardy. Viniendo de un matemático desconocido, Hardy pensó en las nueve páginas manuscritas que recibió de Ramanujan como un posible "fraude". Reconoció algunas de las fórmulas de Ramanujan, pero otras le "parecían casi imposibles de creer". Uno de estos teoremas que Hardy encontró casi imposibles de creer estaba en la parte inferior de la página tres (válido para 0  < a < b + 1/2):

Hardy también quedó impresionado por algunos de los trabajos de Ramanujan en relación con las series infinitas:

El primer resultado ya había sido determinado por un matemático llamado Bauer. El segundo era nuevo para Hardy, y se deriva de una clase de funciones llamadas series hipergeométricas que primero habían sido investigadas por Leonhard Euler y Carl Friedrich Gauss. En comparación con el trabajo de Ramanujan en integrales, Hardy encontró estos resultados "mucho más intrigantes". Después vio los teoremas de Ramanujan en fracciones continuas en la última página de los manuscritos, y comentó que "[los teoremas] me derrotaron por completo, yo nunca había visto antes nada parecido en absoluto". Se imaginó que los teoremas de Ramanujan "deben ser verdad, porque, si no eran ciertos, nadie tendría la imaginación necesaria para inventárselos". Hardy pidió a un colega, J. E. Littlewood, que mirase el manuscrito. Littlewood quedó sorprendido por el genio matemático de Ramanujan. Después de estudiar el escrito con Littlewood, Hardy llegó a la conclusión de que las cartas eran "sin duda lo más notable que he recibido", y comentaron que Ramanujan era "un matemático de la más alta calidad, un hombre de originalidad y capacidad totalmente excepcionales". Un colega, E. H. Neville, posteriormente comentó que "ni uno solo de los [teorema]s podría haberse incluido en el examen de matemáticas más avanzado del mundo".

El 8 de febrero de 1913, Hardy escribió una carta a Ramanujan, expresando su interés por su trabajo. Hardy también añadió que era "esencial que yo vea pruebas de algunas de sus afirmaciones". Antes de que su carta llegase a Madrás durante la tercera semana de febrero, Hardy se puso en contacto con la Oficina de la India para planificar el viaje de Ramanujan a Cambridge. Arthur Davies, Secretario del Comité Asesor para los Estudiantes de la India, se reunió con Ramanujan para organizar su viaje a Inglaterra. Sin embargo, de acuerdo con su educación brahmán, Ramanujan se negó en principio a salir de su país para "ir a un país extranjero". Mientras tanto, Ramanujan envió una nueva carta a Hardy con teoremas, en la que le decía que "He encontrado un amigo en ti que ve mi trabajo con simpatía."

Para complementar el respaldo de Hardy, un exprofesor de matemáticas en el Trinity College de Cambridge, Gilbert Walker, pudo ver el trabajo de Ramanujan y expresó su asombro, instándolo a pasar un tiempo en Cambridge. Como resultado de la aprobación de Walker, B. Hanumantha Rao, profesor de matemáticas en una universidad de ingeniería, invitó a Narayana Iyer a una reunión de la Junta de Estudios de Matemáticas para discutir "lo que podemos hacer por S. Ramanujan". La junta acordó conceder a Ramanujan una beca de investigación de 75 rupias por mes durante los siguientes dos años en la Universidad de Madrás. Mientras estuvo contratado como estudiante de investigación, Ramanujan continuó presentando trabajos a la Revista de la Sociedad Matemática de la India. En un caso, Narayana Iyer presentó algunos teoremas de Ramanujan relativos a la suma de una serie a la revista, añadiendo que "El siguiente teorema se debe a S. Ramanujan, estudiante de matemáticas de la Universidad de Madrás". Más tarde, en noviembre, el profesor británico Edward B. Ross del Christian College de Madrás, a quien Ramanujan había conocido unos años antes, irrumpió en su clase un día con sus ojos brillantes, preguntando a sus estudiantes "¿Sabe Ramanujan polaco?" La razón era que en un artículo, Ramanujan había anticipado el trabajo de un matemático polaco cuya ponencia acababa de llegar en el correo del día. En sus trabajos trimestrales, Ramanujan elaboró teoremas para resolver integrales definidas con mayor facilidad. Trabajó sobre el teorema integral de Giuliano Frullani publicado en 1821, formulando generalizaciones que se podían hacer para evaluar integrales anteriormente inabordables.

La correspondencia de Hardy con Ramanujan se agrió después de que Ramanujan se negase a viajar a Inglaterra. Hardy encargó a un colega que estaba dando conferencias en Madrás, E.H. Neville, que convenciese a Ramanujan para ir a Inglaterra. Neville preguntó a Ramanujan que por qué no quería ir a Cambridge. Al parecer, Ramanujan ahora había aceptado la propuesta; como Neville dijo, "Ramanujan no necesitaba ser convencido, y la oposición de sus padres había sido retirada". Al parecer, la madre de Ramanujan tuvo un sueño vívido en el que la diosa de la familia, Namagiri Thayar, le ordenó que "no prolongase más tiempo la separación entre su hijo y el cumplimiento del propósito de su vida". Ramanujan se embarcó por fin hacia Inglaterra, dejando a su esposa con sus padres en la India.

Estancia en Inglaterra

Ramanujan (centro) con otros científicos en el Trinity College

Whewell's Court, Trinity College, Cambridge

Ramanujan embarcó en el SS Nevasa el 17 de marzo de 1914. A las 10 de la mañana, el barco partió de Madrás. Llegó a Londres el 14 de abril, con EH Neville esperándole con un coche. Cuatro días después, Neville lo llevó a su casa en Chesterton Road, en Cambridge. Ramanujan comenzó inmediatamente su trabajo con Littlewood y Hardy. Después de seis semanas, se mudó de la casa de Neville y fijó su residencia en Whewell Court, a solo cinco minutos a pie de la habitación de Hardy. Hardy y Littlewood comenzaron a echar un vistazo a los cuadernos de Ramanujan. El propio Hardy ya había recibido 120 teoremas de Ramanujan en las dos primeras cartas, pero había muchos más resultados y teoremas en los cuadernos. Vio que algunos estaban equivocados, otros ya habían sido descubiertos, pero el resto eran nuevas ideas originales. Ramanujan causó una profunda impresión en Hardy y en Littlewood, quien comentó: "Creo que es al menos un nuevo Jacobi", mientras Hardy dijo que "Se le puede comparar únicamente con [Leonhard] Euler o Jacobi."

Ramanujan pasó casi cinco años en Cambridge colaborando con Hardy y Littlewood, y publicó una parte de sus hallazgos allí. Hardy y Ramanujan tenían personalidades totalmente contrapuestas. Su colaboración fue un choque de diferentes culturas, creencias y estilos de trabajo. Hardy era ateo y un apóstol de la prueba y el rigor matemático, mientras que Ramanujan era un hombre profundamente religioso y se apoyaba fuertemente en su intuición. Mientras que Ramanujan permaneció en Inglaterra, Hardy hizo todo lo posible para llenar las lagunas en la educación de su colega sin interrumpir su hechizo de inspiración.

Ramanujan fue galardonado con una licenciatura en Ciencias (este grado fue más tarde renombrado PhD) en marzo de 1916 por su trabajo de investigación en números altamente compuestos, la primera parte de la cual fue publicada como un documento en las Actas de la London Mathematical Society. El artículo tenía más de 50 páginas con la demostración de diferentes propiedades de tales números pero debido a una escasez de papel ocasionada por la Primera Guerra Mundial no se terminó de publicar sino hasta 1997 en "The Ramanujan Journal". Hardy comentó que Ramanujan mostró un extraordinario ingenio en su manejo pero a pesar de ello no hizo que esta área de conocimientos fuera algo interesante, en su opinión.

El 6 de diciembre de 1917, fue elegido miembro de la Sociedad Matemática de Londres. Fue nombrado miembro de la Royal Society en 1918, convirtiéndose en el segundo indio en conseguirlo, tras Ardaseer Cursetjee en 1841, a los 31 años, siendo uno de los estudiosos más jóvenes en la historia de la Royal Society. Resultó elegido "por su investigación en Funciones Elípticas y en la Teoría de Números." El 13 de octubre de 1918, se convirtió en el primer indio elegido miembro del Trinity College.

Enfermedad y muerte

Plagado de problemas de salud durante toda su vida, viviendo en un país lejos de su hogar y obsesivamente involucrado con sus matemáticas, la salud de Ramanujan empeoró en Inglaterra, tal vez exacerbada por el estrés y por la escasez de su dieta vegetariana durante la Primera Guerra Mundial. Fue diagnosticado de tuberculosis y de una deficiencia vitamínica grave, y fue internado en un sanatorio.

Ramanujan volvió a Kumbakonam en 1919 y murió poco después a la edad de 32 años, en 1920. Su viuda, S. Janaki Ammal, se trasladó a Bombay, pero volvió a Chennai (antes Madrás) en 1950, donde vivió hasta su muerte a los 95 años, en 1994.

Un análisis de la historia clínica de Ramanujan y sus síntomas elaborado en 1994 por el doctor D.A.B Young llegó a la conclusión de que era mucho más probable que tuviese amebiasis hepática, una infección parasitaria del hígado generalizada en Madrás, donde Ramanujan había pasado gran parte de su vida. Tuvo dos episodios de disentería antes de abandonar la India. Cuando no se trata adecuadamente, la disentería puede permanecer latente por años y dar lugar a la amebiasis hepática, una enfermedad difícil de diagnosticar, pero fácilmente curable una vez que se diagnostica.

Personalidad y vida espiritual

Ramanujan ha sido descrito como una persona con una disposición un tanto tímida y tranquila, un hombre digno con agradables maneras. Llevaba una vida bastante espartana mientras estuvo en Cambridge. Los primeros biógrafos indios de Ramanujan lo describen como rigurosamente ortodoxo en cuestiones religiosas. Ramanujan atribuía su perspicacia a su deidad familiar, "Mahalakshmi de Namakkal". Buscó la inspiración en su obra, y afirmó que alguna vez soñó con gotas de sangre que simbolizaban a "Narasimha", el consorte masculino de su deidad familiar, recibiendo a continuación visiones de rollos de contenido matemático complejo que se desarrollaban ante sus ojos. A menudo decía que «una ecuación para mí no tiene sentido, a menos que represente un pensamiento de Dios».

Hardy cita a Ramanujan haciendo énfasis en que todas las religiones le parecían igualmente verdaderas, argumentando además que la religiosidad de Ramanujan había sido idealizada por los occidentales, y exagerada —en lo referente a sus creencias, no a su práctica— por sus biógrafos indios. Al mismo tiempo, destacó la estricta observancia de Ramanujan del vegetarianismo.

Logros matemáticos

En matemáticas, hay una diferencia entre tener una idea y tener una prueba. El talento de Ramanujan sugirió una gran cantidad de fórmulas que podrían entonces ser investigadas en profundidad más adelante. G. H. Hardy señaló que los descubrimientos de Ramanujan eran inusualmente ricos y que a menudo tenían muchas más implicaciones que las que se observaban a primera vista. Como consecuencias indirectas, normalmente se abrían nuevas direcciones de investigación. Los ejemplos más interesantes de estas fórmulas incluyen intrigantes series infinitas para pi, como la que se da a continuación:

Este resultado se basa en el discriminante fundamental negativo d = -4 × 58 = -232 con número de clase h (d) = 2 (teniendo en cuenta que 5 × 7 × 13 × 58 = 26.390 y que 9.801 = 99 × 99; 396 = 4 × 99) y se relaciona con el hecho de que

Puede compararse con los números de Heegner, que tienen número de clase 1 y producen fórmulas similares. La serie de Ramanujan para pi converge extraordinariamente rápido (de forma exponencial) y constituye la base de algunos de los algoritmos más rápidos que actualmente se utilizan para calcular el valor de pi. Ya el primer término de la suma da , una aproximación de pi que es correcta con seis cifras decimales. Al respecto, se pueden también ver las series de Ramanujan-Sato, con carácter más general. Jonathan y Peter Borwein han demostrado recientemente la validez de esta fórmula descubierta por Ramanujan en 1910 (como era habitual, sin facilitar una demostración).

Una de sus capacidades más notables fue la rápida solución de problemas. En el período en el que compartía una habitación con P. C. Mahalanobis, este le planteó un problema: "Imagina que estás en una calle con casas marcadas del 1 al n. Hay una casa en el medio (x) tal que la suma de los números de la casa a la izquierda de la misma es igual a la suma de los números de las casas a su derecha. Si n está entre 50 y 500, ¿cuánto valen n y x?" Este es un problema de dos variables con múltiples soluciones. Ramanujan lo pensó y dio la respuesta con una peculiaridad: ideó una fracción continua. Lo inusual fue que era una solución válida para toda una clase de problemas. Mahalanobis se sorprendió y le preguntó cómo lo había hecho. "Es simple. En el momento en que escuché el problema, yo sabía que la respuesta era una fracción continua. ¿Qué fracción continua? me pregunté a mí mismo. Entonces la respuesta vino a mi mente", le contestó Ramanujan.

Su intuición también le llevó a obtener alguna identidad previamente desconocida, como:

para todo , donde es la función gamma, en relación con un valor especial de la función eta de Dedekind. Haciendo el desarrollo en serie de potencias e igualando los coeficientes de , y resultan algunas identidades profundas de la secante hiperbólica.

En 1918, Hardy y Ramanujan estudiaron la función de partición P(n) ampliamente y dieron una serie asintótica no convergente que permite el cálculo exacto del número de particiones de un entero. Hans Rademacher, en 1937, fue capaz de refinar su fórmula para encontrar una solución exacta a este problema mediante una serie convergente. El trabajo de Ramanujan y de Hardy en esta área dio lugar a un nuevo método de gran alcance para la búsqueda de fórmulas asintóticas, llamado el Método del círculo de Hardy-Littlewood.

Descubrió la función theta simulada en el último año de su vida. Durante muchos años estas funciones fueron un misterio, pero ahora se sabe que son las partes holomorfas armónicas débiles de las formas de Maass.

Ramanujan es célebre por su extraordinaria productividad en materia de fórmulas. G. H. Hardy declaró, haciendo alusión a Leonhard Euler, también un gran creador de fórmulas extraordinarias, que "Ramanujan había nacido 200 años demasiado tarde". Respecto a las fórmulas contenidas en la carta que recibió del matemático indio en 1913, afirmaba como ya se ha señalado anteriormente que "eran demasiado increíbles para ser falsas":

Dos ejemplos espectaculares de su creatividad son las fórmulas siguientes :

relacionando el número áureo, con una fracción continua generalizada y poniendo en juego e y π;

Esta segunda fórmula combina una série infinita y una fracción continua generalizada, estableciendo una relación entre las dos más conocidas constantes matemáticas.

De un género un poco diferente, descubrió la asombrosa identidad siguiente, que permite construir ejemplos de la suma de tres cubos equivalente a un cuarto cubo:

;

esta igualdad, que generaliza la curiosa coincidencia numérica de que 3³ + 4³ + 5³ = 6³ = 216, es fácil de verificar mediante un sencillo desarrollo algebraico, pero parece imposible de obtener sin disponer de una teoría general. Una vez más, no está claro si Ramanujan disponía de esta teoría.

La conjetura de Ramanujan

Aunque hay numerosas declaraciones que podrían haber llevado el nombre de conjetura de Ramanujan, hay una declaración que fue muy influyente en trabajos posteriores. En particular, la conexión de esta conjetura con conjeturas de André Weil en la geometría algebraica abrió nuevas áreas de investigación. Esta conjetura es una afirmación sobre el tamaño de la función tau, que sirve para generar la forma modular discriminante Δ(q), una forma de cúspide típica en la teoría de formas modulares. Finalmente fue probada en 1973, como consecuencia de la prueba de Pierre Deligne de las conjeturas de Weil. Las etapas de reducción implicadas son muy complejas. Deligne ganó una Medalla Fields en 1978 por su trabajo en las conjeturas de Weil.

Cuadernos de Ramanujan

Todavía en Madrás, Ramanujan registró la mayor parte de sus resultados en cuatro cuadernos de papel de hojas arrancables. Estos resultados fueron en su mayoría redactados sin demostraciones. Este es probablemente el origen de la percepción errónea de que Ramanujan era incapaz de probar sus resultados y simplemente pensaba en ellos hasta dar con el resultado final directamente. El matemático Bruce C. Berndt, en su revisión de estos cuadernos y trabajos, afirma que Ramanujan sin duda era capaz de demostrar la mayoría de sus resultados, pero decidió no hacerlo.

Este estilo de trabajo puede haber tenido varias razones. Dado que el papel era muy caro, Ramanujan haría la mayor parte de su trabajo y tal vez de sus pruebas en una pizarra, y luego transfería solo los resultados definitivos al papel. Utilizar una pizarra era común entre los estudiantes de matemáticas de la Madras Presidency en aquella época. También era bastante probable que hubiera sido influido por el estilo del libro de G. S. Carr estudiado en su juventud, que contenía resultados pero sin demostraciones. Por último, es posible que Ramanujan consideraba sus trabajos únicamente de su propio interés personal; y por lo tanto solo registraba los resultados.

La primera libreta tiene 351 páginas con 16 capítulos bastante organizados y algún material no organizado; el segundo cuaderno tiene 256 páginas en 21 capítulos y 100 páginas no organizadas; y el tercer cuaderno contiene 33 páginas no organizadas. Los resultados de sus cuadernos inspiraron numerosos trabajos de matemáticos posteriores tratando de demostrar lo que él había encontrado. El propio Hardy ideó trabajos que exploran el material de trabajo de Ramanujan, como hicieron G. N. Watson, B. M. Wilson, y Bruce Berndt. Un cuarto cuaderno con 87 páginas no organizadas, el llamado "cuaderno perdido", fue redescubierto en 1976 por George Andrews.

Los cuadernos 1, 2 y 3 se publicaron como un conjunto de dos volúmenes en 1957 por el Instituto Tata de Investigación Fundamental (TIFR ), Mumbai, India. Esta fue una edición fotocopiada de los manuscritos originales, de su puño y letra.

En diciembre de 2011, como parte de las celebraciones del 125 aniversario del nacimiento de Ramanujan, TIFR publicó los cuadernos a color en dos volúmenes en una edición de coleccionista. Se reprodujeron a partir de imágenes escaneadas y microfilmados de los manuscritos originales por los expertos archiveros de la Biblioteca de Investigación Roja Muthiah de Chennai.

Hardy, Ramanujan y el número 1729

El número 1729 se conoce como el número de Hardy-Ramanujan por una famosa anécdota del matemático británico G. H. Hardy en relación con una visita al hospital para ver a Ramanujan. En palabras de Hardy:

Recuerdo una vez que fui a verle cuando estaba enfermo en Putney. Había viajado en el taxi número 1729 y mencioné que me parecía un número poco notable, y que esperaba que esto no fuera un mal presagio. "No", me respondió, "es un número muy interesante; es el número más pequeño expresable como la suma de dos cubos de dos maneras diferentes".

En efecto, la cifra tiene dos descomposiciones diferentes:

Las generalizaciones de esta idea han creado la noción de "número taxicab" y de "número cabtaxi".

Coincidentemente, 1729 es también un número de Carmichael.

Otros puntos de vista de los matemáticos sobre Ramanujan

Fotografía de Srinivasa Ramanujan

Hardy dijo: «Combinó un poder de generalización, una idea de la forma y una capacidad de modificar rápidamente sus hipótesis que, a menudo, eran realmente sorprendentes, y lo hizo, en su propio campo peculiar, sin rival en su día. La limitación de sus conocimientos era tan sorprendente como su profundidad. He aquí un hombre que podía elaborar ecuaciones modulares y teoremas... en órdenes desconocidos, cuyo dominio de las fracciones continuas fue... más allá del de cualquier matemático en el mundo, que había encontrado por sí mismo la ecuación funcional de la función zeta y los términos dominantes de muchos de los problemas más famosos de la teoría analítica de los números, y sin embargo, nunca había oído hablar de una función doblemente periódica o del teorema de Cauchy, y que tenía de hecho una vaga idea de lo que era una función de variable compleja...". Cuando se le preguntó sobre los métodos empleados por Ramanujan para llegar a sus soluciones, Hardy dijo que "llegaban a través de un proceso de argumentación mezclada, de intuición y de inducción, de la que fue enteramente incapaz de dar ninguna explicación coherente." También declaró que "nunca conoció a su igual, y se le podía comparar únicamente con Euler o Jacobi."

K. Srinivasa Rao, manifestó que "En cuanto a su lugar en el mundo de las matemáticas, citamos a Bruce C. Berndt, quien dijo: 'Paul Erdos nos ha pasado las calificaciones personales de Hardy sobre distintos matemáticos. Supongamos que valoramos a los matemáticos sobre la base de su talento puro en una escala de 0 a 100; Hardy se dio una puntuación de 25, J. E. Littlewood obtuvo 30, David Hilbert 80, y Ramanujan tendría 100.'"

El profesor Bruce C. Berndt de la Universidad de Illinois, durante una conferencia en el IIT de Madrás en mayo de 2011 declaró que en los últimos 40 años, como casi todos los teoremas de Ramanujan le han dado la razón, se había producido un mayor aprecio por el trabajo y la brillantez de Ramanujan. Además, afirmó que el trabajo de Ramanujan estaba ahora omnipresente en muchas áreas de la matemática moderna y de la física.

En su libro Scientific Edge, el físico Jayant Narlikar habló de "Srinivasa Ramanujan, descubierto por el matemático de Cambridge Hardy, cuyos grandes hallazgos matemáticos estaban empezando a apreciarse entre 1915 y 1919. Sus logros pasaron a ser plenamente comprendidos mucho más tarde, pasados muchos años de su prematura muerte en 1920. Por ejemplo, su trabajo en números altamente compuestos (números con un gran número de factores) iniciaron una nueva línea de investigación en la teoría de tales números".

Durante su tarea de toda una vida dedicada a la educación y la propagación de las matemáticas entre los niños en edad escolar en la India, Nigeria y otros países, P. K. Srinivasan introdujo continuamente obras matemáticas de Ramanujan.

Reconocimiento póstumo

Busto de Ramanujan en el jardín del Birla Industrial & Technological Museum.

• El estado natal de Ramanujan de Tamil Nadu celebra cada 22 de diciembre el aniversario del nacimiento de Ramanujan como "Día Estatal de TI", rememorando tanto al hombre y sus logros, como a un nativo de Tamil Nadu.
• Un sello de correos que representa a Ramanujan fue emitido por el Gobierno de la India en 1962 -en el 75 aniversario del nacimiento de Ramanujan- conmemorando sus logros en el campo de la teoría de números, y un nuevo diseño fue emitido el 26 de diciembre de 2011, por el Servicio de Correos de la India.
• El "Ramanujan Journal" (Diario de Ramanujan) es una publicación internacional que se lanzó con el propósito de dar a conocer el trabajo en todas las áreas de las matemáticas influenciadas por su trabajo.
• Desde el año del Centenario de Ramanujan, el 22 de diciembre de cada año, se celebra el Día de Ramanujan en el Government Arts College de Kumbakonam donde había estudiado. La celebración es organizada por el Departamento de Matemáticas mediante la celebración de un seminario de dos o tres días invitando a eminentes estudiosos de universidades y colegios. Los participantes son principalmente estudiantes de matemáticas, investigadores y profesores de las universidades locales. El cumpleaños número 125 fue celebrado de una manera especial, invitando a eminentes eruditos matemáticos extranjeros como G. E. Andrews y Bruce C. Berndt, especialistas muy familiarizados con las aportaciones y trabajos de Ramanujan.
• El Indian Institute of Technology (IIT) de Madrás en Chennai, conmemora el trabajo y la vida de Ramanujan cada 22 de diciembre. El Departamento de Matemáticas celebra este día mediante la organización de un Simposio Nacional sobre Métodos Matemáticos y Aplicaciones (NSMMA) durante un día, invitando a eminentes eruditos indios y extranjeros.
• Se ha creado un premio para jóvenes matemáticos de países en desarrollo con el nombre de Ramanujan por el Centro Internacional de Física Teórica (CIFT), en cooperación con el Unión Matemática Internacional, que nombra a los miembros del comité del premio.
• El Shanmugha Arts, Science, Technology & Research Academy (SASTRA), con sede en el estado de Tamil Nadu, en el sur de la India, ha instituido el "SASTRA Ramanujan Prize" dotado con 10 000 dólares para ser otorgado anualmente a un matemático que no exceda de los 32 años y que haya hecho contribuciones sobresalientes en un área de la matemática influida por la obra de Ramanujan. El límite de edad se refiere a los años que vivió Ramanujan, cuyos abundantes logros siguen siendo la base de nuevas realizaciones. Este premio ha sido otorgado anualmente desde 2005, en una conferencia internacional promovida por SASTRA en Kumbakonam, la ciudad natal de Ramanujan, alrededor de la fecha de su cumpleaños el 22 de diciembre.
• En 2012, con motivo del 125 aniversario de su nacimiento, la India declaró el cumpleaños de Ramanujan (22 de diciembre), como el "Día Nacional de las Matemáticas". La declaración fue hecha por el doctor Manmohan Singh en Chennai el 26 de diciembre de 2011, quien también expresó que el año 2012 se celebraría el "Año Matemático Nacional" en la India.
• La residencia de Ramanujan es conservada por la universidad SASTRA en Kumbakonam.

En la cultura popular

• En 2013 se produjo una película basada en el libro The Man Who Knew Infinity: La vida del genio Ramanujan, de Robert Kanigel, con Matt Brown dirigiendo su propio guion escrito. Dev Patel interpretaba a Srinivasa Ramanujan, Jeremy Irons encarnó a G. H. Hardy y Devika Bhise a su esposa. Fue presentada al Festival de Cannes. El rodaje de Ramanujan comenzó el 3 de agosto de 2014 en el Trinity College, Cambridge.
• La película de producción indo-británica 'Ramanujan' relata la vida de Ramanujan y fue grabada simultáneamente en idioma inglés y en idioma tamil Fue lanzada en 2014 por la compañía de cine independiente 'Camphor Cinema'.
• La obra de teatro First Class Man montada por Alter Ego Productions, está basada en el libro del mismo título de David Freeman. La trama se centra alrededor de Ramanujan y su relación compleja y disfuncional con Hardy. El 16 de octubre de 2011, se anunció que Roger Spottiswoode, conocido por su película de James Bond El mañana nunca muere, estaba trabajando en la versión cinematográfica, protagonizada por el actor indio Siddharth. Al igual que el libro y la obra teatral también se iba a titular First Class Man.
• A Disappearing Number es una producción británica de la compañía Complicite que explora la relación entre Hardy y Ramanujan.
• La novela The Indian Clerk de David Leavitt explora en la ficción los acontecimientos subsiguientes de la carta de Ramanujan a Hardy.
• Google le honró en el 125 aniversario de su nacimiento mediante la sustitución de su logotipo con un doodle en su página principal.
• Ramanujan era mencionado en la película de 1997 Good Will Hunting, en una escena en la que el profesor Gerald Lambeau (Stellan Skarsgard) explica a Sean Maguire (Robin Williams) el genio de Will Hunting (Matt Damon) al compararlo con Ramanujan.
• El 22 de marzo de 1988, la serie de la PBS Nova emitió un documental sobre Ramanujan, "El hombre que amaba los números" (Temporada 15, Episodio 19).
• La serie de televisión Numb3rs incluye el personaje de la Dra. Amita Ramanujan, una profesora de matemáticas aplicadas cuyo nombre homenajea la obra de Ramanujan.
• La historia de Ramanujan es la referencia de la que se hizo eco Cyril M. Kornbluth en su relato de 1954 titulado simplemente "Gómez".

Véase también

En inglés: Srinivasa Ramanujan Facts for Kids

Publicaciones de Ramanujan seleccionadas

• Srinivasa Ramanujan, G. H. Hardy, P. V. Seshu Aiyar, B. M. Wilson, Bruce C. Berndt (2000). Collected Papers of Srinivasa Ramanujan. AMS. ISBN 0-8218-2076-1. 

Libro publicado originalmente en el año 1927 después de la muerte de Ramanujan. Contiene los 37 artículos publicados en revistas profesionales de Ramanujan durante su vida. La tercera reimpresión contiene comentarios adicionales por Bruce C. Berndt.

• S. Ramanujan (1957). Notebooks (2 Volumes). Bombay: Tata Institute of Fundamental Research. 

Libros que contienen fotocopias de los cuadernos originales manuscritos por Ramanujan.

• S. Ramanujan (1988). The Lost Notebook and Other Unpublished Papers. New Delhi: Narosa. ISBN 3-540-18726-X. 

Libro que contiene fotocopias de las páginas del "Lost Notebook".

• , Revista de la Sociedad India de Matemáticas.
• S. Ramanujan (2012). Notebooks (2 Volumes). Bombay: Tata Institute of Fundamental Research. 

Producido a partir de imágenes escaneadas y microfilmadas de los manuscritos originales de los archiveros de expertos de la Biblioteca de Investigación Roja Muthiah, de Chennai.

Selección de publicaciones sobre Ramanujan y su obra

• Berndt, Bruce C. (1998). Butzer, P. L.; Oberschelp, W.; Jongen, H. Th., ed. Charlemagne and His Heritage: 1200 Years of Civilization and Science in Europe (PDF). Turnhout, Belgium: Brepols Verlag. pp. 119-146. ISBN 2-503-50673-9. 
• Berndt, Bruce C.; Andrews, George E. (2005). Ramanujan's Lost Notebook. Part I. New York: Springer. ISBN 0-387-25529-X. 
• Berndt, Bruce C.; Andrews, George E. (2008). Ramanujan's Lost Notebook. Part II. New York: Springer. ISBN 978-0-387-77765-8. 
• Berndt, Bruce C.; Andrews, George E. (2012). Ramanujan's Lost Notebook. Part III. New York: Springer. ISBN 978-1-4614-3809-0. 
• Berndt, Bruce C.; Andrews, George E. (2013). Ramanujan's Lost Notebook. Part IV. New York: Springer. ISBN 978-1-4614-4080-2. 
• Berndt, Bruce C.; Rankin, Robert A. (1995). Ramanujan: Letters and Commentary 9. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-0287-9. 
• Berndt, Bruce C.; Rankin, Robert A. (2001). Ramanujan: Essays and Surveys 22. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-2624-7. 
• Berndt, Bruce C. (2006). Number Theory in the Spirit of Ramanujan 9. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-4178-5. 
• Berndt, Bruce C. (1985). Ramanujan's Notebooks. Part I. New York: Springer. ISBN 0-387-96110-0. 
• Berndt, Bruce C. (1999). Ramanujan's Notebooks. Part II. New York: Springer. ISBN 0-387-96794-X. 
• Berndt, Bruce C. (2004). Ramanujan's Notebooks. Part III. New York: Springer. ISBN 0-387-97503-9. 
• Berndt, Bruce C. (1993). Ramanujan's Notebooks. Part IV. New York: Springer. ISBN 0-387-94109-6. 
• Berndt, Bruce C. (2005). Ramanujan's Notebooks. Part V. New York: Springer. ISBN 0-387-94941-0. 
• Hardy, G. H. (1978). Ramanujan. New York: Chelsea Pub. Co. ISBN 0-8284-0136-5. 
• Hardy, G. H. (1999). Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-2023-0. 
• Henderson, Harry (1995). Modern Mathematicians. New York: Facts on File Inc. ISBN 0-8160-3235-1. 
• Kanigel, Robert (1991). The Man Who Knew Infinity: a Life of the Genius Ramanujan. New York: Charles Scribner's Sons. ISBN 0-684-19259-4. 
• Kolata, Gina (19 de junio de 1987). «Remembering a 'Magical Genius'». Science, New Series (American Association for the Advancement of Science) 236 (4808): 1519-1521. doi:10.1126/science.236.4808.1519. 
• Leavitt, David (2007). The Indian Clerk (de bolsillo edición). London: Bloomsbury. ISBN 978-0-7475-9370-6. 
• Narlikar, Jayant V. (2003). Scientific Edge: the Indian Scientist From Vedic to Modern Times. New Delhi, India: Penguin Books. ISBN 0-14-303028-0. 
• Sankaran, T. M. (2005). Srinivasa Ramanujan- Ganitha lokathile Mahaprathibha (en malayalam). Kochi, India: Kerala Sastra Sahithya Parishath.