robot de la enciclopedia para niños

Sistema hexadecimal para niños

Enciclopedia para niños
No debe confundirse con sistema sexagesimal.
Archivo:Hexadecimal-counting
Cómo contar en hexadecimal usando 8 dedos

El sistema hexadecimal (a veces abreviado como hex.) es una forma de contar que usa 16 símbolos diferentes. A diferencia de nuestro sistema decimal que usa 10 números (del 0 al 9), el sistema hexadecimal usa los números del 0 al 9 y también las letras de la A a la F.

Este sistema es muy importante en el mundo de la informática y las ciencias de la computación. Las computadoras usan el sistema binario (solo 0s y 1s), pero el hexadecimal es una forma más corta y fácil para que los programadores representen grandes cantidades de información binaria. Por ejemplo, un "byte" (una unidad básica de memoria en computadoras) puede representarse con solo dos dígitos hexadecimales.

Los símbolos que se usan en el sistema hexadecimal son:

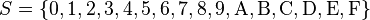
S = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{F}\}\,

Cada letra tiene un valor numérico específico en nuestro sistema decimal:

  • A = 10
  • B = 11
  • C = 12
  • D = 13
  • E = 14
  • F = 15

A veces, se usan letras minúsculas en lugar de mayúsculas. Al igual que en el sistema decimal, el valor de cada dígito en un número hexadecimal depende de su posición. Cada posición representa una potencia de 16.

Por ejemplo, para entender el número hexadecimal 3E0A16 en nuestro sistema decimal:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3E0A_{16} = 3 \cdot 16^3 + E \cdot 16^2 + 0 \cdot 16^1 + A \cdot 16^0 = Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \cdot 4096 + 14 \cdot 256 + 0 \cdot 16 + 10 \cdot 1 = 15882

El sistema hexadecimal que usamos hoy en día en las computadoras fue presentado por primera vez por la empresa IBM en 1963.

¿Cómo se relaciona el hexadecimal con otros sistemas?

El sistema hexadecimal está muy conectado con otros sistemas numéricos que usan las computadoras, como el binario (base 2) y el octal (base 8). Aquí puedes ver cómo se corresponden los números en estos sistemas:

0hex = 0dec = 0oct 0 0 0 0
1hex = 1dec = 1oct 0 0 0 1
2hex = 2dec = 2oct 0 0 1 0
3hex = 3dec = 3oct 0 0 1 1
4hex = 4dec = 4oct 0 1 0 0
5hex = 5dec = 5oct 0 1 0 1
6hex = 6dec = 6oct 0 1 1 0
7hex = 7dec = 7oct 0 1 1 1
8hex = 8dec = 10oct 1 0 0 0
9hex = 9dec = 11oct 1 0 0 1
Ahex = 10dec = 12oct 1 0 1 0
Bhex = 11dec = 13oct 1 0 1 1
Chex = 12dec = 14oct 1 1 0 0
Dhex = 13dec = 15oct 1 1 0 1
Ehex = 14dec = 16oct 1 1 1 0
Fhex = 15dec = 17oct 1 1 1 1

Fracciones en hexadecimal

Así como tenemos fracciones en el sistema decimal (como 1/2 o 1/3), también existen en el sistema hexadecimal. Algunas fracciones tienen una representación exacta y otras son "periódicas", lo que significa que sus dígitos se repiten infinitamente.

Fracción Hexadecimal Resultado en hexadecimal
1/2 1/2 0,8
1/3 1/3 0,5 periódico
1/4 1/4 0,4
1/5 1/5 0,3 periódico
1/6 1/6 0,2A periódico
1/7 1/7 0,249 periódico
1/8 1/8 0,2
1/9 1/9 0,1C7 periódico
1/10 1/A 0,19 periódico
1/11 1/B 0,1745D periódico
1/12 1/C 0,15 periódico
1/13 1/D 0,13B periódico
1/14 1/E 0,1249 periódico
1/15 1/F 0,1 periódico
1/16 1/10 0,1

Para convertir un número decimal con fracciones a hexadecimal, puedes multiplicar la parte decimal por 16 repetidamente. Por ejemplo, para convertir 0,06640625 (decimal) a hexadecimal:

  • Multiplicamos 0,06640625 por 16, lo que da 1,0625. El primer dígito hexadecimal es 1.
  • Tomamos la parte decimal de 1,0625 (que es 0,0625) y la multiplicamos por 16, lo que da 1. El siguiente dígito hexadecimal es 1.
  • Como el resultado es un número entero (1), hemos terminado.

Así, 0,06640625 en decimal es 0,11 en hexadecimal.

Operaciones matemáticas en hexadecimal

Podemos sumar, restar y multiplicar números en sistema hexadecimal, de forma similar a como lo hacemos en el sistema decimal, pero recordando que la base es 16 y que usamos letras para los números del 10 al 15.

Hexadecimal Decimal
A 10
B 11
C 12
D 13
E 14
F 15

Suma hexadecimal

Cuando sumamos en hexadecimal, si el resultado es 16 o más, restamos 16 y "llevamos" 1 a la siguiente columna, igual que cuando sumamos en decimal y el resultado es 10 o más.

  • 9 + 7 = 16 (en decimal). En hexadecimal, 16 es 10. Así que escribimos 0 y "llevamos" 1.
  • A + 6 = 16 (en decimal). Como A es 10, 10 + 6 = 16. En hexadecimal, esto es 10. Escribimos 0 y "llevamos" 1.
  • A + A = 20 (en decimal). Como A es 10, 10 + 10 = 20. Restamos 16 (20 - 16 = 4). Escribimos 4 y "llevamos" 1. El resultado es 14.
  • F + E = 29 (en decimal). Como F es 15 y E es 14, 15 + 14 = 29. Restamos 16 (29 - 16 = 13). El número 13 en hexadecimal es D. Escribimos D y "llevamos" 1. El resultado es 1D.

Resta hexadecimal

La resta en hexadecimal puede hacerse de varias maneras, una de ellas es usando el método de "complemento". Es un poco más complejo, pero el resultado final es el mismo que con la resta tradicional.

Por ejemplo, para restar A4FC9 - DE8: 1. Aseguramos que ambos números tengan la misma cantidad de dígitos, añadiendo ceros al principio del número más corto: A4FC9 - 00DE8. 2. Calculamos el "complemento" del segundo número. Esto implica restar cada dígito del número más grande posible (F, que es 15). 3. Luego, sumamos el primer número con este "complemento". 4. Finalmente, ajustamos el resultado para obtener la respuesta correcta.

El resultado de A4FC9 - DE8 es A41E1. Puedes usar una calculadora científica para verificar estos resultados.

Multiplicación hexadecimal

La multiplicación en hexadecimal sigue el mismo proceso que en el sistema decimal, pero usando una tabla de multiplicar hexadecimal.

  1 2 3 4 5 6 7 8 9 A B C D E F 10
1 1 2 3 4 5 6 7 8 9 A B C D E F 10
2 2 4 6 8 A C E 10 12 14 16 18 1A 1C 1E 20
3 3 6 9 C F 12 15 18 1B 1E 21 24 27 2A 2D 30
4 4 8 C 10 14 18 1C 20 24 28 2C 30 34 38 3C 40
5 5 A F 14 19 1E 23 28 2D 32 37 3C 41 46 4B 50
6 6 C 12 18 1E 24 2A 30 36 3C 42 48 4E 54 5A 60
7 7 E 15 1C 23 2A 31 38 3F 46 4E 54 5D 62 69 70
8 8 10 18 20 28 30 38 40 48 50 58 60 68 70 78 80
9 9 12 1B 24 2D 36 3F 48 51 5A 63 6C 75 7E 87 90
A A 14 1E 28 32 3C 46 50 5A 64 6E 78 82 8C 96 A0
B B 16 21 2C 37 42 4E 58 63 6E 79 84 8F 9A A5 B0
C C 18 24 30 3C 48 54 60 6C 78 84 90 9C A8 B4 C0
D D 1A 27 34 41 4E 5D 68 75 82 8F 9C A9 B6 C3 D0
E E 1C 2A 38 46 54 62 70 7E 8C 9A A8 B6 C4 D2 E0
F F 1E 2D 3C 4B 5A 69 78 87 96 A5 B4 C3 D2 E1 F0
10 10 20 30 40 50 60 70 80 90 A0 B0 C0 D0 E0 F0 100

Galería de imágenes

  • Hexadecimal-counting

    Cómo contar en hexadecimal usando 8 dedos

Véase también

Kids robot.svg En inglés: Hexadecimal Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Sistema_hexadecimal&oldid=4980831»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Sistema hexadecimal para Niños. Enciclopedia Kiddle.