Distribución normal para niños
Datos para niños Distribución normal |
||
|---|---|---|
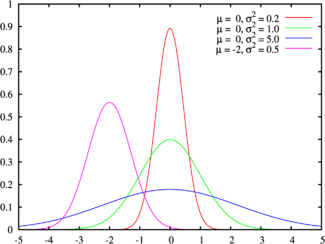 La línea verde corresponde a la distribución normal estándar Función de densidad de probabilidad |
||
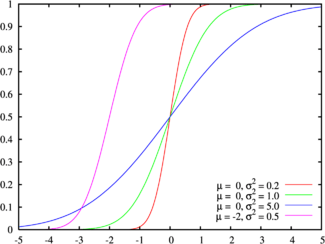 Función de distribución de probabilidad |
||
| Parámetros |
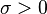 |
|
| Dominio | 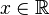 |
|
| Función de densidad (pdf) |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac1{\sigma\sqrt{2\pi</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END-->\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}} \,\! |cdf = En estadística y probabilidad, la distribución normal es una de las distribuciones de probabilidad más importantes. También se le conoce como distribución de Gauss o distribución gaussiana. Es un tipo de distribución para variable continua, lo que significa que puede tomar cualquier valor dentro de un rango. La gráfica de esta distribución tiene una forma de campana, por eso se le llama la campana de Gauss. Es simétrica, lo que significa que si la doblas por la mitad, ambos lados coinciden. Esta distribución es muy útil porque nos ayuda a entender y predecir muchos fenómenos en la naturaleza, la sociedad y la psicología. Aunque a veces no sabemos por qué ocurren ciertos eventos, la distribución normal puede explicarlos si pensamos que son el resultado de muchas pequeñas causas independientes que se suman. También es importante para un método llamado mínimos cuadrados, que se usa para encontrar la mejor línea que se ajusta a un conjunto de datos. Contenido¿Dónde podemos ver la distribución normal?La distribución normal aparece en muchos lugares. Aquí tienes algunos ejemplos:
Además, la distribución normal es fundamental en la estadística. Por ejemplo, si tomas muchas muestras de una población y calculas el promedio de cada muestra, esos promedios tienden a seguir una distribución normal, incluso si la población original no la sigue. Esto es cierto si las muestras son lo suficientemente grandes. Historia de la distribución normalLa idea de la distribución normal fue presentada por primera vez por un matemático llamado Abraham de Moivre en 1733. Él la descubrió mientras estudiaba cómo se comportaba la distribución binomial cuando se trabajaba con números muy grandes. Más tarde, otro gran matemático, Laplace, amplió el trabajo de De Moivre en 1812. Hoy, a esta combinación de sus descubrimientos se le conoce como el Teorema de De Moivre-Laplace. Gauss, un matemático muy famoso, también usó mucho esta distribución para analizar datos de astronomía. Por eso, su nombre se asoció a ella, aunque De Moivre la descubrió primero. Esto es un ejemplo de la ley de Stigler, que dice que los descubrimientos a menudo no llevan el nombre de su descubridor original. El nombre de "campana" para la forma de la gráfica fue usado por primera vez por Esprit Jouffret en 1872. El término "distribución normal" fue dado por varios científicos alrededor de 1875. ¿Qué es la media y la desviación típica?Para entender la distribución normal, necesitamos conocer dos valores importantes:
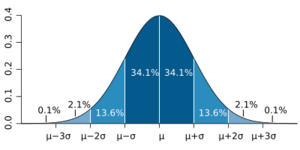
Propiedades de la distribución normalAquí te contamos algunas características importantes de la distribución normal:
* Alrededor del 68.26% de los datos están a una distancia de una desviación típica ( Estandarización de variables normalesPodemos transformar cualquier distribución normal en una distribución normal estándar. Esta es una versión especial donde la media es 0 y la desviación típica es 1. Esto se hace con una fórmula sencilla: El Teorema del Límite CentralEl Teorema del límite central es una idea muy poderosa en estadística. Dice que si sumas un gran número de variables aleatorias (que no tienen por qué ser normales), el resultado de esa suma se parecerá mucho a una distribución normal. Esto es importante porque nos ayuda a usar la distribución normal para aproximar otras distribuciones, como:
Archivo:Normal approximation to binomial.svg ¿Por qué es tan común la distribución normal?La distribución normal aparece en muchos lugares porque, como explica el Teorema del Límite Central, cuando muchas pequeñas causas actúan juntas y se suman, el resultado tiende a ser normal. Sin embargo, a veces las causas actúan de forma multiplicativa, no aditiva. En esos casos, el logaritmo de la variable es el que sigue una distribución normal, y la variable original sigue una distribución log-normal. Aquí hay más ejemplos de dónde se ve la distribución normal:
Uso en computaciónPara las simulaciones por ordenador, a veces necesitamos generar números que sigan una distribución normal. Hay varios métodos para hacer esto:
Galería de imágenesVéase también
|
|


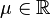
![\frac12\left[1 + \operatorname{erf}\left( \frac{x-\mu}{\sigma\sqrt{2}}\right)\right]](/images/math/1/8/4/1843c9e5cfa016ce2bbcc852dedc9e00.png) |media =
|media = 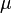 |mediana =
|mediana = 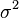 |simetría = 0 |curtosis = 0 |entropía =
|simetría = 0 |curtosis = 0 |entropía = 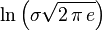 |mgf =
|mgf = 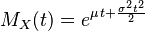 |car =
|car = 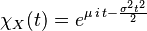 }}
}}
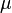 ): Es el promedio de todos los datos. En la distribución normal, la media es el centro de la campana. También es la
): Es el promedio de todos los datos. En la distribución normal, la media es el centro de la campana. También es la 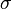 ): Nos dice qué tan dispersos están los datos alrededor de la media. Si la desviación típica es pequeña, los datos están muy juntos. Si es grande, están más separados.
): Nos dice qué tan dispersos están los datos alrededor de la media. Si la desviación típica es pequeña, los datos están muy juntos. Si es grande, están más separados.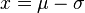 y
y 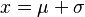 .
.
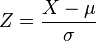 Donde X es tu dato,
Donde X es tu dato, 

 En inglés:
En inglés: