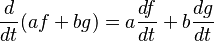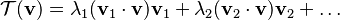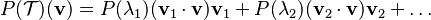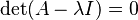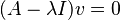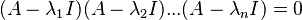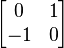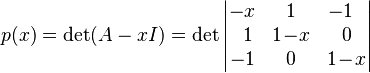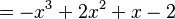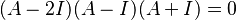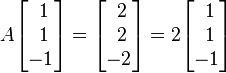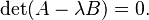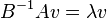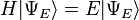Vector, valor y espacio propios para niños

En álgebra lineal, los vectores propios, eigenvectores o autovectores de un operador lineal son los vectores no nulos que, cuando son transformados por el operador, dan lugar a un múltiplo escalar de sí mismos, con lo que no cambian su dirección. Este escalar  recibe el nombre valor propio, autovalor o valor característico. A menudo, una transformación queda completamente determinada por sus vectores propios y valores propios. Un espacio propio, autoespacio o subespacio fundamental asociado al valor propio
recibe el nombre valor propio, autovalor o valor característico. A menudo, una transformación queda completamente determinada por sus vectores propios y valores propios. Un espacio propio, autoespacio o subespacio fundamental asociado al valor propio  es el conjunto de vectores propios con un valor propio común.
es el conjunto de vectores propios con un valor propio común.
Contenido
- Etimología
- Introducción
- Ejemplos
- Casos de interés especial
- Ecuación del valor propio
- Teorema espectral
- Vectores propios y valores propios de matrices
- Espacios de dimensión infinita
- Aplicaciones
- Véase también
Etimología
La palabra alemana eigen (/'aj γen /), que se traduce en español como propio, se usó por primera vez en este contexto por David Hilbert en 1904 (aunque Helmholtz la usó previamente con un significado parecido). Eigen se ha traducido también como inherente, característico o el prefijo auto-, donde se aprecia el énfasis en la importancia de los valores propios para definir la naturaleza única de una determinada transformación lineal. Las denominaciones vector y valor característicos también se utilizan habitualmente. El uso del prefijo auto- es un caso propio y singular que se da solamente en español, portugués e italiano. En otras lenguas con más tradición en Matemáticas (alemán, neerlandés, inglés, francés, ruso, etc.) nadie parece haber traducido eigen- (propio, perteneciente a, etc.) por auto- (que nada tiene que ver con la etimología o el significado del prefijo eigen).
Introducción
Las transformaciones lineales del espacio —como la rotación, la reflexión, el ensanchamiento, o cualquier combinación de las anteriores; en esta lista podrían incluirse otras transformaciones— pueden interpretarse mediante el efecto que producen en los vectores. Los vectores pueden visualizarse como flechas de una cierta longitud apuntando en una dirección y sentido determinados.
- Los vectores propios de las transformaciones lineales son vectores que, o no son afectados por la transformación o solo resultan multiplicados por un escalar; y, por tanto, no varían su dirección.
- El valor propio de un vector propio es el factor de escala por el que ha sido multiplicado.
- Un espacio propio es un espacio formado por todos los vectores propios del mismo valor propio, además del vector nulo, que no es un vector propio.
- La multiplicidad geométrica de un valor propio es la dimensión del espacio propio asociado.
- El espectro de una transformación en espacios vectoriales finitos es el conjunto de todos sus valores propios.
Por ejemplo, un vector propio de una rotación en tres dimensiones es un vector situado en el eje de rotación sobre el cual se realiza la rotación. El valor propio correspondiente es 1 y el espacio propio es el eje de giro. Como es un espacio de una dimensión, su multiplicidad geométrica es uno. Es el único valor propio del espectro (de esta rotación) que es un número real.
Definición
Formalmente, se definen los vectores propios y valores propios de la siguiente manera:
Sea 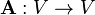 un operador lineal en un cierto
un operador lineal en un cierto 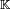 -espacio vectorial
-espacio vectorial  y
y 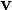 un vector no nulo en
un vector no nulo en  . Si existe un escalar
. Si existe un escalar  tal que
tal que
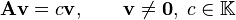
entonces decimos que 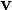 es un vector propio del operador A, y su valor propio asociado es
es un vector propio del operador A, y su valor propio asociado es  . Observe que si
. Observe que si 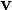 es un vector propio con el valor propio
es un vector propio con el valor propio  entonces cualquier múltiplo diferente de cero de
entonces cualquier múltiplo diferente de cero de 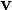 es también un vector propio con el valor propio
es también un vector propio con el valor propio  . De hecho, todos los vectores propios con el valor propio asociado
. De hecho, todos los vectores propios con el valor propio asociado  junto con 0, forman un subespacio de V, el «espacio propio» para el valor propio
junto con 0, forman un subespacio de V, el «espacio propio» para el valor propio  . Observe además que un espacio propio
. Observe además que un espacio propio 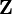 es un subespacio invariante de
es un subespacio invariante de 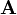 , es decir dado un vector
, es decir dado un vector 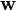 en
en 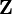 , el vector
, el vector 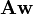 también pertenece a
también pertenece a 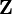 .
.
Ejemplos
A medida que la Tierra rota, los vectores en el eje de rotación permanecen invariantes. Si se considera la transformación lineal que sufre la Tierra tras una hora de rotación, una flecha que partiera del centro de la Tierra al polo Sur geográfico sería un vector propio de esta transformación, pero una flecha que partiera del centro a un punto del ecuador no sería un vector propio. Dado que la flecha que apunta al polo no cambia de longitud por la rotación, su valor propio es 1.
Otro ejemplo sería una lámina de metal que se expandiera uniformemente a partir de un punto de tal manera que las distancias desde cualquier punto al punto fijo se duplicasen. Esta expansión es una transformación con valor propio 2. Cada vector desde el punto fijo a cualquier otro es un vector propio, y el espacio propio es el conjunto de todos esos vectores.

Sin embargo, el espacio geométrico tridimensional no es el único espacio vectorial. Por ejemplo, considérese una cuerda sujeta por sus extremos, como la de un instrumento de cuerda (mostrada a la derecha). La distancia de los átomos de la cuerda vibrante desde sus posiciones cuando ésta está en reposo pueden interpretarse como componentes de un vector en el espacio con tantas dimensiones como átomos tenga dicha cuerda.
Si se supone que la cuerda es un medio continuo y se considera la transformación de la cuerda en el transcurso del tiempo, sus vectores propios o funciones propias son sus ondas estacionarias—lo que, mediante la intervención del aire circundante, se puede interpretar como el resultado de tañer una guitarra. Las ondas estacionarias corresponden a oscilaciones particulares de la cuerda tales que la forma de la cuerda se escala por un factor (el valor propio) con el paso del tiempo. Cada componente del vector asociado con la cuerda se multiplica por este factor dependiente del tiempo. Las amplitudes (valores propios) de las ondas estacionarias decrecen con el tiempo si se considera la atenuación. En este caso se puede asociar un tiempo de vida al vector propio, y relacionar el concepto de vector propio con el concepto de resonancia.
Casos de interés especial
Intuitivamente, para las transformaciones lineales del espacio de dos dimensiones 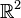 , los vectores propios son:
, los vectores propios son:
- rotación: ningún vector propio de valores reales (existen en cambio pares valor propio, vector propio complejos).
- reflexión: los vectores propios son perpendiculares y paralelos al eje de simetría, los valores propios son -1 y 1, respectivamente.
- escalado uniforme: todos los vectores son vectores propios, y el valor propio es el factor de escala.
- proyección sobre una recta: los vectores propios con el valor propio 1 son paralelos a la línea, vectores propios con el valor propio 0 son perpendiculares a la dirección de la proyección
Ecuación del valor propio
Matemáticamente, vλ es un vector propio y λ el valor propio correspondiente de una transformación T si verifica la ecuación:
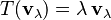
donde T(vλ) es el vector obtenido al aplicar la transformación T a vλ.
Supóngase que T es una transformación lineal (lo que significa que 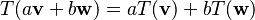 para todos los escalares a, b, y los vectores v, w). Considérese una base en ese espacio vectorial. Entonces, T y vλ pueden representarse en relación a esa base mediante una matriz AT y un vector columna vλ—un vector vertical unidimensional. La ecuación de valor propio en esta representación matricial se representa de la siguiente forma:
para todos los escalares a, b, y los vectores v, w). Considérese una base en ese espacio vectorial. Entonces, T y vλ pueden representarse en relación a esa base mediante una matriz AT y un vector columna vλ—un vector vertical unidimensional. La ecuación de valor propio en esta representación matricial se representa de la siguiente forma:
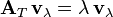
donde la yuxtaposición es un producto de matrices. Dado que en esta circunstancia la transformación T y su representación matricial AT son equivalentes, a menudo podemos emplear solo T para la representación matricial y la transformación. Esto es equivalente a un conjunto de n combinaciones lineales, donde n es el número de vectores de la base. En esta ecuación, tanto el valor propio λ y las n componentes de vλ son desconocidos. Sin embargo, a veces es poco natural o incluso imposible escribir la ecuación de valor propio en forma matricial. Esto ocurre, por ejemplo, cuando el espacio vectorial es de dimensión infinita, como por ejemplo en el caso de la cuerda mostrada anteriormente. Dependiendo de la naturaleza de la transformación T y el espacio al que se aplica, puede ser ventajoso representar la ecuación de valor propio como un conjunto de ecuaciones diferenciales, donde los vectores propios reciben a menudo el nombre de autofunciones del operador diferencial que representa a T. Por ejemplo, la derivación misma es una transformación lineal, ya que (si f(t) y g(t) son funciones derivables y a y b son constantes)
Considérese la diferenciación con respecto a 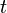 . Sus autofunciones h(t) obedecen a la ecuación de valor propio:
. Sus autofunciones h(t) obedecen a la ecuación de valor propio:
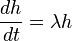 ,
,
donde λ es el autovalor asociado con la función. Una función en el tiempo es constante si  , crece proporcionalmente a sí misma si
, crece proporcionalmente a sí misma si  es positiva, y decrece proporcionalmente a sí misma si
es positiva, y decrece proporcionalmente a sí misma si  es negativa. Por ejemplo, una población ideal de conejos engendra con más frecuencia a medida que hay más conejos, y por tanto satisface la ecuación para lambda positivo.
es negativa. Por ejemplo, una población ideal de conejos engendra con más frecuencia a medida que hay más conejos, y por tanto satisface la ecuación para lambda positivo.
La solución a la ecuación de valor propio es 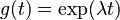 , la función exponencial; pues esa función es una función propia del operador diferencial d/dt con el valor propio λ. Si λ es negativa, la evolución de g se denomina decaimiento exponencial; si es positiva se denomina crecimiento exponencial. El valor de λ puede ser cualquier número complejo. El espectro de d/dt es entonces el plano complejo en su totalidad. En este ejemplo el espacio vectorial en el que actúa d/dt es el espacio de las funciones derivables de una variable. Este espacio tiene una dimensión infinita (pues no es posible expresar cada función diferenciable como combinación lineal de un número finito de funciones base). No obstante, el espacio propio asociado a un valor propio determinado λ es unidimensional. Es el conjunto de todas las funciones
, la función exponencial; pues esa función es una función propia del operador diferencial d/dt con el valor propio λ. Si λ es negativa, la evolución de g se denomina decaimiento exponencial; si es positiva se denomina crecimiento exponencial. El valor de λ puede ser cualquier número complejo. El espectro de d/dt es entonces el plano complejo en su totalidad. En este ejemplo el espacio vectorial en el que actúa d/dt es el espacio de las funciones derivables de una variable. Este espacio tiene una dimensión infinita (pues no es posible expresar cada función diferenciable como combinación lineal de un número finito de funciones base). No obstante, el espacio propio asociado a un valor propio determinado λ es unidimensional. Es el conjunto de todas las funciones 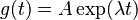 , donde A es una constante arbitraria, la población inicial en t=0.
, donde A es una constante arbitraria, la población inicial en t=0.
Teorema espectral
El teorema espectral muestra la importancia de los valores propios y vectores propios para caracterizar una transformación lineal de forma única. En su versión más simple, el teorema espectral establece que, bajo unas condiciones determinadas, una transformación lineal puede expresarse como la combinación lineal de los vectores propios con coeficientes de valor igual a los valores propios por el producto escalar de los vectores propios por el vector al que se aplica la transformación, lo que puede escribirse como:
donde 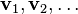 y
y 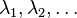 representan a los vectores propios y valores propios de
representan a los vectores propios y valores propios de 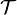 . El caso más simple en el que tiene validez el teorema es cuando la transformación lineal viene dada por una matriz simétrica real o una matriz hermítica compleja.
. El caso más simple en el que tiene validez el teorema es cuando la transformación lineal viene dada por una matriz simétrica real o una matriz hermítica compleja.
Si se define la enésima potencia de una transformación como el resultado de aplicarla n veces sucesivas, se puede definir también el polinomio de las transformaciones. Una versión más general del teorema es que cualquier polinomio P de 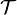 es igual a:
es igual a:
El teorema puede extenderse a otras funciones o transformaciones tales como funciones analíticas, siendo el caso más general las funciones de Borel.
Vectores propios y valores propios de matrices
Cálculo de valores propios y vectores propios de matrices
Si se quiere calcular los valores propios de una matriz dada y ésta es pequeña, se puede calcular simbólicamente usando el polinomio característico. Sin embargo, a menudo resulta imposible para matrices extensas, caso en el que se debe usar un método numérico.
Cálculo simbólico
- Cálculo de los valores propios
Una herramienta importante para encontrar valores propios de matrices cuadradas es el polinomio característico: decir que λ es un valor propio de A es equivalente a decir que el sistema de ecuaciones lineales A v = λ v → A v - λ v = 0 (factorizando por v queda) (A - λI) v = 0 (donde I es la matriz identidad) tiene una solución no nula v (un vector propio), y de esta forma es equivalente al determinante:
La función p(λ) = det(A - λI) es un polinomio de λ pues los determinantes se definen como sumas de productos. Este es el polinomio característico de A: los valores propios de una matriz son los ceros de su polinomio característico.
Todos los valores propios de una matriz A pueden calcularse resolviendo la ecuación 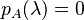 .
.
Si A es una matriz n×n, entonces 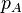 tiene grado n y A tiene como máximo n valores propios.
tiene grado n y A tiene como máximo n valores propios.
El teorema fundamental del álgebra dice que esta ecuación tiene exactamente n raíces (ceros), teniendo en cuenta su multiplicidad. Todos los polinomios reales de grado impar tienen un número real como raíz, así que para n impar toda matriz real tiene al menos un valor propio real. En el caso de las matrices reales, para n par e impar, los valores propios no reales son pares conjugados.
- Cálculo de los vectores propios
Una vez que se conocen los valores propios λ, los vectores propios se pueden hallar resolviendo el sistema de ecuaciones homogéneo:
Una forma más sencilla de obtener vectores propios sin resolver un sistema de ecuaciones lineales se basa en el teorema de Cayley-Hamilton que establece que cada matriz cuadrada satisface su propio polinomio característico. Así, si 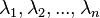 son los valores propios de A se cumple que
son los valores propios de A se cumple que
por lo que los vectores columna de 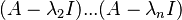 son vectores propios de
son vectores propios de 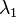 .
.
Un ejemplo de matriz sin valores propios reales es la rotación de 90 grados en el sentido de las manecillas del reloj:
cuyo polinomio característico es 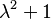 y sus valores propios son el par de conjugados complejos i, -i. Los vectores propios asociados tampoco son reales.
y sus valores propios son el par de conjugados complejos i, -i. Los vectores propios asociados tampoco son reales.
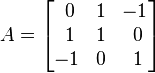
Considérese la matriz
que representa un operador lineal R³ → R³. Si se desea computar todos los valores propios de A, se podría empezar determinando el polinomio característico:
y porque p(x) = - (x - 2)(x - 1)(x + 1) se ve que los valores propios de A son 2, 1 y -1. El teorema de Cayley-Hamilton establece que cada matriz cuadrada satisface su propio polinomio característico. Es decir
Efectivamente, para el caso del valor propio 2, se puede comprobar que
de donde (1, 1, -1) es un vector propio asociado a 2.
Cálculo numérico
En la práctica, los valores propios de las matrices extensas no se calculan usando el polinomio característico. Calcular el polinomio resulta muy costoso, y extraer las raíces exactas de un polinomio de grado alto puede ser difícil de calcular y expresar: el teorema de Abel-Ruffini implica que las raíces de los polinomios de grado alto (5 o superior) no pueden expresarse usándose simplemente raíces enésimas. Existen algoritmos eficientes para aproximar raíces de polinomios, pero pequeños errores en la estimación de los valores propios pueden dar lugar a errores grandes en los vectores propios. En consecuencia, los algoritmos generales para encontrar vectores propios y valores propios son iterativos. La manera más fácil es el método de las potencias: se escoge un vector aleatorio 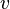 y se calcula una secuencia de vectores unitarios:
y se calcula una secuencia de vectores unitarios:
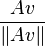 ,
, 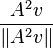 ,
, 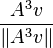 ,...
,...
Esta sucesión casi siempre convergerá a un vector propio correspondiente al mayor valor propio. Este algoritmo es sencillo, pero no demasiado útil aisladamente. Sin embargo, hay métodos más populares, como la descomposición QR, que se basan en él.
Propiedades
Multiplicidad algebraica
La multiplicidad algebraica de un valor propio λ de A es el orden de λ como cero del polinomio característico de A; en otras palabras, si λ es una de las raíces del polinomio, es el número de factores (t − λ) en el polinomio característico tras la factorización. Una matriz n×n, con entradas complejas, tiene n valores propios, contados de acuerdo con su multiplicidad algebraica, ya que su polinomio característico tiene grado n.
Un valor propio de multiplicidad algebraica 1 recibe el nombre de "valor propio simple".
Por ejemplo, se pueden encontrar exposiciones como la siguiente en artículos de teoría de matrices:
- "los valores propios de una matriz A son 4,4,3,3,3,2,2,1,"
lo que significa que la multiplicidad algebraica de 4 es dos, la de 3 es tres, la de 2 es dos y la de 1 es uno. Se emplea este estilo porque la multiplicidad algebraica es la clave de muchas demostraciones matemáticas en teoría de matrices.
Anteriormente se ha definido la multiplicidad geométrica de un valor propio como la dimensión del espacio propio asociado, o el núcleo (espacio propio de los vectores propios del valor propio nulo) de λI - A. La multiplicidad algebraica también puede entenderse como una dimensión: es la dimensión del espacio propio generalizado (1.er sentido) asociado, que es el núcleo de la matriz (λI - A)k para k suficientemente grande. Es decir, es el espacio de los vectores propios generalizados (1.er sentido), donde un vector propio generalizado es cualquier vector que toma valor 0 sí λI - A se aplica suficientes veces en sucesión. Cualquier vector propio es un vector propio generalizado, así que cualquier espacio propio está contenido en el espacio propio generalizado asociado. Esto proporciona una demostración simple de que la multiplicidad geométrica es siempre menor o igual a la algebraica. El primer sentido no debe de confundirse con el problema de valores propios generalizados tal y como se muestra más adelante.
Por ejemplo:
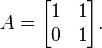
Solo tiene un valor propio λ = 1. El polinomio característico es  , así que este valor propio tiene multiplicidad algebraica 2. Sin embargo, el espacio propio asociado es el eje, que normalmente recibe el nombre de eje x, generado por el vector unitario
, así que este valor propio tiene multiplicidad algebraica 2. Sin embargo, el espacio propio asociado es el eje, que normalmente recibe el nombre de eje x, generado por el vector unitario 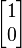 , así que la multiplicidad geométrica es 1.
, así que la multiplicidad geométrica es 1.
Los vectores propios generalizados pueden usarse para calcular la forma normal de Jordan de una matriz (comentado más adelante). El hecho de que los bloques de Jordan en general no son diagonales sino nilpotentes está directamente relacionado con la distinción entre vectores propios y vectores propios generalizados.
Teoremas de descomposición para matrices generales
El teorema de descomposición es una versión del teorema espectral en una clase concreta de matrices. Este teorema se explica normalmente en términos de transformación coordinada. Si U es una matriz invertible, puede verse como una transformación entre un sistema de coordenadas a otro, donde las columnas de U son las componentes de la nueva base de vectores expresados en términos de la base anterior. En este nuevo sistema las coordenadas del vector 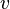 se representan por
se representan por 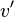 , que puede obtenerse mediante la relación
, que puede obtenerse mediante la relación  y, por otra parte, se tiene
y, por otra parte, se tiene 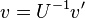 . Aplicando sucesivamente
. Aplicando sucesivamente  ,
,  y
y 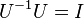 , a la relación
, a la relación  proporciona
proporciona 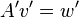 con
con 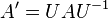 , la representación de A en la nueva base. En esta situación, se dice que las matrices A y
, la representación de A en la nueva base. En esta situación, se dice que las matrices A y 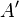 son semejantes.
son semejantes.
El teorema de descomposición declara que, si se eligen como columnas de 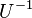 n vectores propios linealmente independientes de A, la nueva matriz
n vectores propios linealmente independientes de A, la nueva matriz 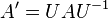 es diagonal y sus elementos en la diagonal son los valores propios de A. Si esto es posible, entonces A es una matriz diagonalizable. Un ejemplo de una matriz no diagonalizable es la matriz A ya mostrada:
es diagonal y sus elementos en la diagonal son los valores propios de A. Si esto es posible, entonces A es una matriz diagonalizable. Un ejemplo de una matriz no diagonalizable es la matriz A ya mostrada:
Hay muchas generalizaciones de esta descomposición que pueden tratar con el caso no diagonalizable, diseñadas con diferentes propósitos:
- la descomposición de Schur declara que toda matriz es equivalente a una matriz triangular.
- la descomposición en valores singulares,
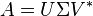 donde
donde  es diagonal con U y V matrices unitarias, los elementos de la diagonal de
es diagonal con U y V matrices unitarias, los elementos de la diagonal de 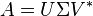 no son negativos y reciben el nombre de valores singulares de A. Esta descomposición también puede hacerse en matrices no cuadradas.
no son negativos y reciben el nombre de valores singulares de A. Esta descomposición también puede hacerse en matrices no cuadradas. - la forma normal de Jordan, donde
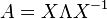 y
y 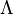 no es diagonal sino diagonal por bloques. El número y tamaño de los bloques de Jordan están determinados por las multiplicidades geométrica y algebraica de los valores propios. La descomposición de Jordan es un resultado fundamental. A partir de ella se puede deducir inmediatamente que una matriz cuadrada está descrita completamente por sus valores propios, incluyendo la multiplicidad. Esto muestra matemáticamente el importante papel que desempeñan los valores propios en el estudio de matrices.
no es diagonal sino diagonal por bloques. El número y tamaño de los bloques de Jordan están determinados por las multiplicidades geométrica y algebraica de los valores propios. La descomposición de Jordan es un resultado fundamental. A partir de ella se puede deducir inmediatamente que una matriz cuadrada está descrita completamente por sus valores propios, incluyendo la multiplicidad. Esto muestra matemáticamente el importante papel que desempeñan los valores propios en el estudio de matrices. - como consecuencia inmediata de la descomposición de Jordan, cualquier matriz A puede escribirse de forma única como A=S + N donde S es diagonalizable, N es nilpotente (por ejemplo, tal que Nq=0 para un cierto q), y S cumple la propiedad conmutativa del producto (SN=NS).
Otras propiedades de los valores propios
El espectro es invariante bajo transformaciones semejantes: las matrices A y P-1AP tienen los mismos valores propios para cualquier matriz A y cualquier matriz invertible P. El espectro es también invariante a la trasposición de las matrices: A y A T tienen los mismos valores propios.
Dado que una transformación lineal en espacios de dimensiones finitas es biyectiva si y solo si es inyectiva, una matriz es invertible si y solo si cero no es un valor propio de la matriz.
Otras consecuencias de la descomposición de Jordan son:
- una matriz es matriz diagonalizable si y solo si las multiplicidades geométrica y algebraica coinciden para todos sus valores propios. En particular una matriz n×n que tiene n valores propios diferentes es siempre diagonalizable;
- Dado que la traza, o la suma de elementos de la diagonal principal de una matriz se preserva en la equivalencia unitaria, la forma normal de Jordan constata que es igual a la suma de sus valores propios.
- De forma similar, dado que los valores propios de una matriz triangular son las entradas de la diagonal principal su determinante es igual al producto de los valores propios (contados de acuerdo con su multiplicidad algebraica).
Algunos ejemplos de la localización del espectro de ciertas subclases de matrices normales son:
- Todos los valores propios de una matriz hermítica (A = A*) son reales. Además, todos los valores propios de una matriz definida positiva son positivos;
- Todos los valores propios de una matriz antihermítica (A = −A*) son imaginarios puros;
- Todos los valores propios de una matriz unitaria (A-1 = A*) tienen valor absoluto uno;
Si A es una matriz m×n con m ≤ n, y B es una matriz n×m, entonces BA tiene los mismos valores propios de AB más n − m valores propios nulos.
A cada matriz se le puede asociar una norma vectorial, que depende de la norma de su dominio, el operador norma de una matriz cuadrada es una cota superior del módulo de sus valores propios, y por tanto de su radio espectral. Esta norma está directamente relacionada con el método de las potencias para calcular el valor propio de mayor módulo. Para matrices normales, el operador norma (la norma euclídea) es el mayor módulo entre de sus valores propios.
Vector propio conjugado
Un vector propio conjugado es un vector que tras la transformación pasa a ser un múltiple escalar de su conjugado, donde el escalar recibe el nombre de valor propio conjugado de la transformación lineal. Los vectores propios y valores propios conjugados representan esencialmente la misma información y significado que los vectores propios y valores propios, pero aparecen cuando se utiliza un sistema de coordenadas alternativo. La ecuación correspondiente es:
Por ejemplo, en teoría de electromagnetismo disperso, la transformación lineal A representa la acción efectuada por el objeto dispersor, y los vectores propios representan los estados de polarización de la onda electromagnética. En óptica, el sistema coordenado se define a partir del punto de vista de la onda, y lleva a una ecuación de valor propio regular, mientras que en radar, el sistema coordenado se define desde el punto de vista del radar, y da lugar a una ecuación de valor propio conjugado.
Problema de valor propio generalizado
Un problema de valor propio generalizado (2º sentido) es de la forma
donde A y B son matrices. Los valores propios generalizados (2º sentido) λ pueden obtenerse resolviendo la ecuación
El conjunto de matrices de la forma  , donde
, donde  es un número complejo, recibe el nombre de lápiz si B es invertible, entonces el problema original puede escribirse en la forma
es un número complejo, recibe el nombre de lápiz si B es invertible, entonces el problema original puede escribirse en la forma
que es un problema de valores propios estándar. Sin embargo, en la mayoría de situaciones es preferible no realizar la inversión, y resolver el problema de valor propio generalizado con la configuración original.
Si A y B son matrices simétricas con entradas reales, entonces los valores propios son reales. Esto se aprecia tan fácilmente a partir de la segunda formulación equivalente, pues la matriz 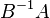 no es necesariamente simétrica si A y B lo son.
no es necesariamente simétrica si A y B lo son.
La aplicación de moleculares orbitales expuesta más adelante proporciona un ejemplo de este caso.
Entradas de un anillo
En una matriz cuadrada A con entradas de un anillo, λ recibe el nombre de valor propio por la derecha si existe un vector columna x tal que Ax=λx, o un valor propio por la izquierda si existe un vector fila no nulo y tal que yA=yλ.
Si el anillo es conmutativo, los valores propios por la izquierda son iguales a los valores propios por la derecha y se les llama simplemente valores propios.
Espacios de dimensión infinita

Si el espacio vectorial es de dimensión infinita, la noción de valores propios puede generalizarse al concepto de espectro. El espectro es el conjunto de escalares λ para el que 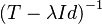 , no está definido, esto es, tal que
, no está definido, esto es, tal que 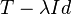 no tiene inversa acotada.
no tiene inversa acotada.
Si λ es un valor propio de T, λ está en el espectro de T. En general, el recíproco no es verdadero. Hay operadores en los espacios de Hilbert o Banach que no tienen vectores propios. Por ejemplo, tómese un desplazamiento bilateral en el espacio de Hilbert 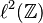 ; ningún vector propio potencial puede ser cuadrado-sumable, así que no existe ninguno. Sin embargo, cualquier operador lineal acotado en un espacio de Banach V tiene espectro no vacío. El espectro
; ningún vector propio potencial puede ser cuadrado-sumable, así que no existe ninguno. Sin embargo, cualquier operador lineal acotado en un espacio de Banach V tiene espectro no vacío. El espectro 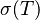 del operador T V → V se define como
del operador T V → V se define como
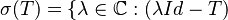 no es invertible
no es invertible
Entonces σ(T) es un conjunto compacto de números complejos, y es no vacío. Cuando T es un operador compacto (y en particular cuando T es un operador entre espacios finito-dimensionales como arriba), el espectro de T es igual que el conjunto de sus valores propios.
En espacios de dimensión infinita, el espectro de un operador acotado es siempre no vacío, lo que también se cumple para operadores adjuntos propios no acotados. A través de su medida espectral, el espectro de cualquier operador adjunto propio, acotado o no, puede descomponerse en sus partes absolutamente continua, discreta, y singular. El crecimiento exponencial proporciona un ejemplo de un espectro continuo, como en el caso anterior de la cuerda vibrante. El átomo de hidrógeno es un ejemplo en el que aparecen ambos tipos de espectro. El estado ligado del átomo de hidrógeno corresponde a la parte discreta del espectro, mientras que el proceso de ionización queda descrito por la parte continua.
Aplicaciones
- Ecuación de Schrödinger

Un ejemplo de una ecuación de valor propio donde la transformación 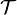 se representa en términos de un operador diferencial es la ecuación de Schrödinger independiente del tiempo de la mecánica cuántica:
se representa en términos de un operador diferencial es la ecuación de Schrödinger independiente del tiempo de la mecánica cuántica:

Donde H, el Hamiltoniano, es un operador diferencial de segundo orden y 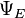 la función de onda, es una de las funciones propias correspondientes al valor propio E, interpretado como la energía.
la función de onda, es una de las funciones propias correspondientes al valor propio E, interpretado como la energía.
Sin embargo, en caso de que solo se busquen soluciones para los estados ligados de la ecuación de Schrödinger, como suele ser el caso en química cuántica, se buscará 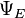 en el espacio de las funciones de cuadrado integrable. Dado que este espacio es un espacio de Hilbert, con un producto escalar bien definido, podemos introducir una base en la que se puede representar
en el espacio de las funciones de cuadrado integrable. Dado que este espacio es un espacio de Hilbert, con un producto escalar bien definido, podemos introducir una base en la que se puede representar 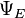 y H como un vector unidimensional y una matriz respectivamente. Esto permite representar la ecuación de Schrödinger en forma matricial.
y H como un vector unidimensional y una matriz respectivamente. Esto permite representar la ecuación de Schrödinger en forma matricial.
La notación bra-ket, utilizada a menudo en este contexto, pone énfasis en la diferencia entre el vector o estado 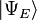 y su representación, la función
y su representación, la función 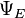 . En este contexto se escribe la ecuación de Schrödinger
. En este contexto se escribe la ecuación de Schrödinger
y se llama a 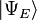 un estado propio de H (que a veces se representa como
un estado propio de H (que a veces se representa como 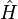 en algunos libros de texto) que puede interpretarse como una transformación en lugar de una representación particular en términos de operadores diferenciales. En la ecuación expuesta,
en algunos libros de texto) que puede interpretarse como una transformación en lugar de una representación particular en términos de operadores diferenciales. En la ecuación expuesta, 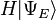 se interpreta como el vector obtenido por aplicación de la transformación H a
se interpreta como el vector obtenido por aplicación de la transformación H a 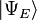 .
.
- Orbitales moleculares
En mecánica cuántica, y en particular en física atómica y molecular, y en el contexto de la teoría de Hartree-Fock, los orbitales atómicos y moleculares pueden definirse por los vectores propios del operador de Fock. Los valores propios correspondientes son interpretados como potenciales de ionización a través del teorema de Koopmans. En este caso, el término vector propio se usa con un significado más general, pues el operador de Fock es explícitamente dependiente de los orbitales y sus valores propios. Si se quiere subrayar este aspecto se habla de ecuación de valores propios implícitos. Tales ecuaciones se resuelven normalmente mediante un proceso iterativo, llamado método de campo consistente propio. En química cuántica a menudo se representa la ecuación de Hartree-Fock en una base no ortogonal. Esta representación particular es un problema de valor propio generalizado que tiene el nombre de ecuaciones de Roothaan.
- Análisis factorial
En análisis factorial, los valores propios de la matriz de covarianza corresponden a los factores, y los valores propios a las cargas. El análisis factorial es una técnica estadística usada en ciencias sociales y mercadotecnia, gestión de producto, investigación operativa y otras ciencias aplicadas que tratan con grandes cantidades de datos. El objetivo es explicar la mayor parte de la variabilidad entre varias variables aleatorias observables en términos de un número menor de variables aleatorias no observables llamadas factores. Las variables aleatorias no observables se modelan como combinaciones lineales de los factores más términos de errores.
- Caras propias
En procesado de imagen, las imágenes procesadas de caras pueden verse como vectores cuyas componentes son la luminancia de cada píxel. La dimensión de este espacio vectorial es el número de píxeles. Los vectores propios de la matriz de covarianza asociada a un conjunto amplio de imágenes normalizadas de rostros se llaman caras propias. Son muy útiles para expresar una imagen de un rostro como la combinación lineal de otras. Las caras propias proporcionan un medio de aplicar compresión de datos a los rostros, para propósitos de biometría.
- Tensor de inercia
En mecánica, los vectores propios del momento de inercia definen los ejes principales de un cuerpo rígido. El tensor de inercia es necesario para determinar la rotación de un cuerpo rígido alrededor de su centro de masa. Los valores propios definen los momentos máximos y mínimos obtenidos mediante el círculo de Mohr.
- Tensor de tensión
En mecánica de sólidos deformables, el tensor de tensión es simétrico, así que puede descomponerse en un tensor diagonal cuyos valores propios en la diagonal y los vectores propios forman una base.
En teoría espectral de grafos, un valor propio de un grafo se define como un valor propio de la matriz de adyacencia del grafo A, o de la matriz Laplaciana del grafo 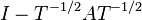 , donde T es una matriz diagonal que contiene el grado de cada vértice, y en
, donde T es una matriz diagonal que contiene el grado de cada vértice, y en 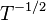 , 0 se substituye por
, 0 se substituye por 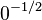 . El vector propio principal de un grafo se usa para medir la centralidad de sus vértices. Un ejemplo es el algoritmo PageRank de Google. El vector propio principal de una matriz de adyacencia modificada del grafo de la web da el page rank en sus componentes.
. El vector propio principal de un grafo se usa para medir la centralidad de sus vértices. Un ejemplo es el algoritmo PageRank de Google. El vector propio principal de una matriz de adyacencia modificada del grafo de la web da el page rank en sus componentes.
Véase también
 En inglés: Eigenvalues and eigenvectors Facts for Kids
En inglés: Eigenvalues and eigenvectors Facts for Kids
- Álgebra lineal
- Aplicación lineal
- Matriz (matemática)
- Operador lineal
- Teorema espectral
- Vector