Matriz definida positiva para niños

Una matriz definida positiva es un tipo especial de matriz que se usa en el álgebra lineal. Piensa en ella como si fuera un número real positivo, pero en el mundo de las matrices. Así como un número positivo es mayor que cero (como 5 o 100), una matriz definida positiva tiene propiedades que la hacen "positiva" en un sentido matemático.

Para que una matriz sea definida positiva, debe ser una matriz hermitiana (o una matriz simétrica si solo trabajamos con números reales). Una matriz hermitiana es una matriz cuadrada que es igual a su propia transpuesta conjugada. En términos más sencillos, es una matriz que tiene una simetría especial.

¿Cómo saber si una matriz es definida positiva?

Una matriz cuadrada M de tamaño n por n (es decir, con n filas y n columnas) se considera definida positiva si cumple con alguna de las siguientes condiciones, que son todas equivalentes:

La prueba del vector

• Si tomas cualquier vector z que no sea cero y haces una operación especial con la matriz M (multiplicando z por la matriz M y luego por el "conjugado transpuesto" de z), el resultado siempre será un número mayor que cero.

* Esto se escribe como: z* M z > 0. * El resultado de esta operación siempre es un número real.

Los autovalores son positivos

• Todos los autovalores de la matriz M son números positivos. Los autovalores son números especiales asociados a una matriz que nos dicen mucho sobre su comportamiento. Para las matrices hermitianas (o simétricas), estos autovalores siempre son números reales.

Define un producto interno

• La matriz M puede usarse para definir un "producto interno". Un producto interno es una forma de multiplicar dos vectores para obtener un número, y tiene propiedades similares a la multiplicación de números, como la propiedad de que el producto de un vector por sí mismo siempre es positivo (a menos que el vector sea cero).

El Criterio de Sylvester

• Todos los "menores principales" de la matriz M son positivos. Los menores principales son los determinantes de las submatrices cuadradas que se forman tomando las primeras filas y columnas de la matriz original.

* Por ejemplo, si tienes una matriz de 3x3, debes revisar: * El determinante de la matriz de 1x1 en la esquina superior izquierda. * El determinante de la matriz de 2x2 en la esquina superior izquierda. * El determinante de la matriz completa de 3x3. * Todos estos determinantes deben ser positivos.

Si la matriz es real y simétrica, las mismas ideas aplican, pero en lugar de usar el "conjugado transpuesto", se usa simplemente la "transpuesta".

Características Importantes

Las matrices definidas positivas tienen varias propiedades útiles:

• Son invertibles: Siempre puedes encontrar su matriz inversa, lo que significa que puedes "deshacer" la operación que la matriz realiza. Su determinante siempre es positivo.
• Su inversa también es definida positiva: Si una matriz es definida positiva, su inversa también lo será.
• Multiplicación por un número positivo: Si multiplicas una matriz definida positiva por un número real positivo, el resultado sigue siendo una matriz definida positiva.
• Suma de matrices: Si sumas dos matrices definidas positivas, el resultado también es una matriz definida positiva.
• Raíz cuadrada: Toda matriz definida positiva tiene una única "raíz cuadrada" matricial. Esto significa que existe otra matriz que, al multiplicarse por sí misma, da como resultado la matriz original.

Otros tipos de matrices

Además de las matrices definidas positivas, existen otras clasificaciones para las matrices hermitianas:

• Definida negativa: Si la operación x* M x siempre da un número negativo para cualquier vector x que no sea cero.
• Semidefinida positiva: Si la operación x* M x siempre da un número mayor o igual a cero para cualquier vector x que no sea cero.
• Semidefinida negativa: Si la operación x* M x siempre da un número menor o igual a cero para cualquier vector x que no sea cero.
• Indefinida: Si no cumple con ninguna de las clasificaciones anteriores. Esto significa que la operación x* M x puede dar resultados positivos para algunos vectores y negativos para otros.

Caso de matrices no simétricas

Una matriz real que no es simétrica también puede tener la propiedad de que x^T M x > 0 para cualquier vector real x que no sea cero. Por ejemplo, la matriz: 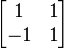cumple con esta propiedad. En general, esto ocurre si la parte simétrica de la matriz (que se calcula como (M + M^T) / 2) es definida positiva.

Véase también

En inglés: Positive-definite matrix Facts for Kids