Función inyectiva para Niños

En matemáticas, una función es como una máquina que toma un valor de entrada y produce un valor de salida. Imagina que tienes dos grupos de cosas: el grupo de "entradas" (llamado dominio) y el grupo de "salidas" (llamado codominio).

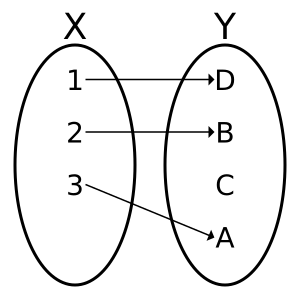
Una función es inyectiva (también conocida como uno a uno) si cada vez que le das una entrada diferente, siempre te da una salida diferente. Es decir, nunca dos entradas distintas producen la misma salida. Piensa en ello como si cada elemento del grupo de "salidas" tuviera como máximo una "entrada" que lo produjo.

Por ejemplo, la función que toma un número y lo eleva al cuadrado (como 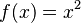$f(x) = x^2$ ) no es inyectiva. ¿Por qué? Porque si le das el número 2, la salida es 4 ( $2^2 = 4$ ). Pero si le das el número -2, la salida también es 4 (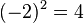 $(-2)^2 = 4$ ). Como 2 y -2 son entradas diferentes que dan la misma salida (4), esta función no es inyectiva.

Sin embargo, si solo consideramos los números positivos para esta función, entonces sí sería inyectiva. Por ejemplo, si solo trabajamos con números como 1, 2, 3, etc., entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1^2=1 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^2=4 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^2=9 , y así sucesivamente. Cada entrada positiva diferente da una salida diferente.

Ejemplo de función inyectiva. Cada punto de la izquierda se conecta con un punto único de la derecha.

Contenido

¿Qué significa que una función sea inyectiva?
Ejemplos de funciones inyectivas y no inyectivas
- La prueba de la línea horizontal
Relación con el tamaño de los conjuntos
Galería de imágenes
Véase también

¿Qué significa que una función sea inyectiva?

Para entenderlo mejor, podemos decir que una función $f$ es inyectiva si, para cualquier par de elementos $a$ y $b$ en el grupo de entradas, si sus salidas son iguales ( $f(a)=f(b)$ ), entonces las entradas también deben ser iguales ( $a=b$ ).

Dicho de otra manera, si las entradas son diferentes (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \neq b ), entonces sus salidas también deben ser diferentes (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(a) \neq f(b) ).

Para demostrar que una función NO es inyectiva, solo necesitas encontrar dos entradas diferentes que produzcan la misma salida.

Ejemplos de funciones inyectivas y no inyectivas

Aquí tienes algunos ejemplos para que lo veas más claro:

La función que toma un número y lo eleva al cubo ( 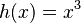$h(x)=x^3$ ) es inyectiva. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^3=8 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-2)^3=-8 . Entradas diferentes dan salidas diferentes.
La función 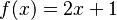$f(x)=2x+1$ es inyectiva. Si tienes dos números diferentes, al multiplicarlos por 2 y sumarles 1, siempre obtendrás resultados diferentes.
Como vimos antes, la función 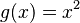$g(x)=x^2$ no es inyectiva porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(1)=1 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(-1)=1 . Las entradas 1 y -1 son diferentes, pero la salida es la misma.
La función exponencial ( 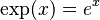$\exp(x)=e^x$ ) es inyectiva. Esto significa que si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^a = e^b , entonces $a$ debe ser igual a $b$ .
La función logaritmo natural ( 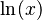$\ln(x)$ ) también es inyectiva.

La prueba de la línea horizontal

Si puedes dibujar la gráfica de una función, hay una forma sencilla de saber si es inyectiva: la prueba de la línea horizontal.

Si dibujas cualquier línea recta horizontal en la gráfica de la función y esta línea cruza la gráfica en más de un punto, entonces la función NO es inyectiva. Si ninguna línea horizontal cruza la gráfica más de una vez, entonces la función SÍ es inyectiva.

Relación con el tamaño de los conjuntos

Si existe una función inyectiva de un conjunto $A$ a un conjunto $B$ , esto nos dice algo sobre el tamaño de los conjuntos. Significa que el número de elementos en el conjunto $A$ (su cardinalidad) es menor o igual que el número de elementos en el conjunto $B$ .

Si además existe una función inyectiva de $B$ a $A$ , entonces podemos asegurar que ambos conjuntos tienen exactamente el mismo número de elementos, es decir, son del mismo tamaño.

Galería de imágenes

Ejemplo de función inyectiva no suprayectiva.

Véase también

En inglés: Injective function Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Función_inyectiva&oldid=4762104»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Función inyectiva para Niños. Enciclopedia Kiddle.

Función inyectiva para niños