Base (álgebra) para niños
En álgebra lineal, una base es como un conjunto especial de "ladrillos" o "vectores" que nos permiten construir cualquier otro vector en un espacio matemático. Imagina que tienes un juego de construcción: una base sería el conjunto mínimo de piezas que necesitas para armar cualquier figura posible en ese juego.
Para que un conjunto de vectores sea una base, debe cumplir dos condiciones importantes:
- Independencia: Ninguno de los vectores de la base puede ser creado combinando los otros vectores de esa misma base. Son únicos y no "dependen" entre sí.
- Generación: Con los vectores de la base, puedes formar cualquier otro vector del espacio combinándolos de diferentes maneras (sumándolos o multiplicándolos por números).
Cuando combinamos los vectores de una base para formar otro vector, los números que usamos para multiplicarlos se llaman "coordenadas" o "componentes" de ese vector en relación con esa base.
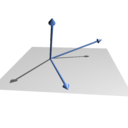
Algo muy interesante es que, aunque un espacio puede tener muchas bases diferentes, ¡todas ellas siempre tienen el mismo número de vectores! A este número lo llamamos la dimensión del espacio vectorial. Por ejemplo, el espacio donde vivimos (el espacio tridimensional) tiene una dimensión de 3, porque necesitamos 3 vectores para formar cualquier punto en él.
Contenido
¿Qué es una Base en Matemáticas?
Una base (a veces llamada "base de Hamel") de un espacio vectorial es un conjunto de vectores que cumple dos reglas fundamentales:
Vectores Independientes: La Clave de una Base
La primera regla es la independencia lineal. Esto significa que si tomas cualquier grupo de vectores de la base, no puedes escribir uno de ellos como una combinación de los otros. Son como piezas únicas que no se pueden reemplazar por otras. Si intentaras sumarlos o restarlos para obtener el vector cero, la única forma de lograrlo sería multiplicando cada vector por cero.
Vectores Generadores: Construyendo el Espacio
La segunda regla es la propiedad generadora. Esto quiere decir que cualquier vector que exista en el espacio puede ser "construido" o "generado" usando los vectores de la base. Es como si los vectores de la base fueran los ingredientes básicos y, al mezclarlos en las cantidades correctas, puedes crear cualquier "receta" (vector) que quieras.
Los números que usas para combinar los vectores de la base se llaman coordenadas o componentes del vector. Lo genial es que, gracias a la independencia lineal, estas coordenadas son siempre únicas para cada vector y cada base.
Bases Ordenadas: Cuando el Orden Importa
A veces, es útil tener un orden específico para los vectores de una base. Por ejemplo, si hablamos de la "primera coordenada" o la "segunda coordenada" de un vector, necesitamos saber a qué vector de la base se refiere cada número. Cuando los vectores de una base tienen un orden fijo, la llamamos base ordenada.
La Dimensión de un Espacio Vectorial
Un hecho muy importante en el álgebra lineal es que, aunque un espacio vectorial puede tener muchas bases diferentes, todas ellas tienen el mismo número de elementos. Este número es tan importante que le damos un nombre especial: la dimensión del espacio vectorial.
Por ejemplo, el plano cartesiano (donde dibujas gráficas con ejes X e Y) tiene una dimensión de 2, porque cualquier punto en él se puede describir con dos números (x, y) y se puede generar con dos vectores base. El espacio tridimensional tiene una dimensión de 3.
- Cualquier conjunto de vectores que pueda generar un espacio vectorial contiene una base.
- Cualquier conjunto de vectores que sea linealmente independiente en un espacio vectorial puede ser completado para formar una base.
Ejemplos de Bases en Diferentes Espacios
- Las bases son conjuntos ordenados. Esto significa que si tienes los vectores {a, b, c} y {b, a, c}, aunque generen el mismo espacio, como bases ordenadas no son iguales.
- Dado un vector y una base, siempre hay una única forma de escribir ese vector usando los elementos de la base.
- Las bases no son únicas. Generalmente, hay infinitas bases diferentes para un mismo espacio vectorial.
Por ejemplo, en el espacio tridimensional (R³), una base muy común y sencilla es la base canónica:
- B_u = {(1,0,0), (0,1,0), (0,0,1)}
Esta base es como los ejes X, Y y Z. Otros ejemplos de bases para R³ son:
- B' = {(2,0,0), (0,1,0), (0,0,1)}
- B = {(1,1,1), (1,1,0), (1,0,0)}
- B = {(504,0,0), (0,7,0), (0,0,1/2)}
En general, cualquier base de R³ estará formada por tres vectores que sean linealmente independientes y que pertenezcan a R³.
- Si un espacio vectorial tiene una dimensión finita, todas sus bases también serán finitas y tendrán la misma cantidad de elementos.
- No todas las bases tienen un número finito de elementos. Por ejemplo, el espacio de los polinomios (como x², x³, etc.) tiene bases con infinitos elementos, como {1, x, x², x³, ...}.
Espacios de Dimensión Finita
Un espacio vectorial de dimensión finita es aquel que puede ser generado por un número limitado de vectores. En estos casos, la dimensión del espacio es simplemente la cantidad de vectores que forman cualquiera de sus bases.
Los subespacios (partes más pequeñas de un espacio vectorial) de un espacio de dimensión finita también tienen bases, y su dimensión es menor que la del espacio más grande. Por ejemplo, una línea recta que pasa por el origen en un plano tiene dimensión uno, porque su base es un solo vector. Esta dimensión es menor que la del plano, que es dos.
Ejemplos de Cálculo de Bases
Veamos cómo encontrar la base de algunos subespacios:
- Ejemplo 1: Una recta en el plano
Consideremos la recta `r` en el plano cartesiano donde `y = x`. Si tomamos cualquier punto `(a,b)` en esta recta, sabemos que `b` debe ser igual a `a`. Entonces, el punto se ve como `(a,a)`. Podemos escribir esto como `a(1,1)`. Esto significa que cualquier punto en la recta `r` se puede obtener multiplicando el vector `(1,1)` por un número `a`. Por lo tanto, el conjunto `{(1,1)}` es una base para esta recta. La recta tiene como base el vector `(1,1)`, que la "dirige" a 45 grados de los ejes.
- Ejemplo 2: Un plano en el espacio tridimensional
Calculemos la base del plano `α` en el espacio tridimensional (R³) donde `x + y + z = 0`. Podemos despejar una variable, por ejemplo, `z = -x - y`. Si tomamos un punto `(a,b,c)` en este plano, podemos escribirlo como `(a,b,-a-b)`. Esto se puede separar en `a(1,0,-1) + b(0,1,-1)`. Así, el conjunto `{(1,0,-1), (0,1,-1)}` es una base para este plano.
- Ejemplo 3: Un subespacio en R⁴
Imagina un subespacio `S` en R⁴ (un espacio de cuatro dimensiones) definido por varias ecuaciones: `x₁ - x₂ = 0`, `x₁ - x₄ = 0` y `5x₁ - 6x₃ - 5x₄ = 0`. Para encontrar la base, resolvemos este sistema de ecuaciones. La solución nos dice que los puntos en `S` son de la forma `(t, t, 0, t)`. Esto se puede escribir como `t(1,1,0,1)`. Por lo tanto, el conjunto que contiene al único vector `{(1,1,0,1)}` es la base de `S`.
- Ejemplo 4: Polinomios
Consideremos un subespacio `P` de polinomios de grado 3, donde `a - b = 0` y `3c + d = 0`. De estas ecuaciones, sabemos que `b = a` y `d = -3c`. Entonces, un polinomio en `P` se ve así: `ax³ + ax² + cx - 3c`. Podemos agrupar los términos: `a(x³ + x²) + c(x - 3)`. Esto significa que cualquier polinomio en `P` se puede formar combinando `(x³ + x²)` y `(x - 3)`. Así, el conjunto `{x³ + x², x - 3}` es una base del espacio `P`.
- Ejemplo 5: Encontrar el espacio generado por una base
Ahora, hagamos lo contrario. Si tenemos una base, por ejemplo, `B = {(1,-1,1)}` para un subespacio de R³, ¿cómo encontramos el espacio que genera? El espacio generado por `B` son todos los puntos `(x,y,z)` que se pueden escribir como `t(1,-1,1)`, donde `t` es un número. Esto nos da un sistema de ecuaciones: `x = t` `y = -t` `z = t` Podemos eliminar `t` de estas ecuaciones. Por ejemplo, de la primera y segunda, `x = -y` (o `x + y = 0`). De la segunda y tercera, `y = -z` (o `y + z = 0`). Entonces, el espacio generado por `B` es el conjunto de todos los puntos `(x,y,z)` en R³ que cumplen `x + y = 0` y `y + z = 0`.
Galería de imágenes
-
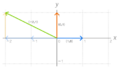
Base estándar en el plano cartesiano (generada a partir de los vectores azul y naranja). El vector verde, sea cual sea, puede ser descrito de forma única en función de los otros dos.
Véase también
 En inglés: Basis (linear algebra) Facts for Kids
En inglés: Basis (linear algebra) Facts for Kids