Operador diferencial para niños
En matemáticas, un operador diferencial es como una instrucción especial que toma una función (que es como una fórmula matemática) y la transforma en otra función. Imagina que es una máquina que, al recibir una función, le aplica una o varias veces la operación de derivada y te entrega una nueva función.
La derivada es una herramienta matemática que nos dice cómo cambia una función en cada punto. Por ejemplo, si tienes una función que describe la posición de un coche en el tiempo, su derivada te dirá la velocidad del coche en cada momento. Un operador diferencial es una forma de escribir y trabajar con estas operaciones de manera más organizada.
Contenido
¿Qué es un Operador Diferencial?
Un operador diferencial es una herramienta matemática que combina la operación de derivada con otras operaciones como la suma y la multiplicación. Se usa para transformar funciones. Piensa en ello como una receta que te dice cómo "cocinar" una función para obtener una nueva.
Por ejemplo, si tienes una función que describe la temperatura en diferentes puntos de una habitación, un operador diferencial podría ayudarte a encontrar cómo cambia la temperatura de un punto a otro.
Cómo se Representan los Operadores
Los operadores diferenciales se suelen escribir usando símbolos especiales. Uno de los más comunes es la letra "D" o "d/dx".
- D o d/dx: Estos símbolos significan "toma la derivada de lo que viene después".
- D² o d²/dx²: Esto significa "toma la derivada dos veces".
Estos operadores pueden ser más complejos, incluyendo varias derivadas y funciones multiplicando.
Operadores con una Sola Variable
Cuando trabajamos con funciones que dependen de una sola variable (por ejemplo, el tiempo o una posición en una línea), los operadores diferenciales son más sencillos.
Notaciones Comunes
Las notaciones más usadas para el operador diferencial son:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {d \over dx}
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): D_x
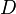
Las primeras dos se usan cuando queremos dejar claro respecto a qué variable estamos derivando (en este caso, 'x'). La última, 'D', se usa cuando ya sabemos por el contexto cuál es la variable.
Para derivadas de órdenes superiores (cuando derivamos varias veces), se usan notaciones como:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d^2}{dx^2}u (derivada de segundo orden)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u'' (otra forma de escribir la derivada de segundo orden)
El Operador Theta
Otro operador interesante es el operador Theta (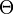 ), que se define como
), que se define como 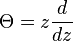 . Este operador es especial porque cuando lo aplicas a una potencia de 'z' (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z^k ), simplemente multiplica la potencia por el exponente: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Theta (z^k) = kz^k Por eso, a veces se le llama el operador de homogeneidad.
. Este operador es especial porque cuando lo aplicas a una potencia de 'z' (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z^k ), simplemente multiplica la potencia por el exponente: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Theta (z^k) = kz^k Por eso, a veces se le llama el operador de homogeneidad.
Operadores Lineales Ordinarios
Muchos operadores diferenciales son "lineales". Esto significa que cumplen dos propiedades importantes:
- Si aplicas el operador a la suma de dos funciones, es lo mismo que aplicar el operador a cada función por separado y luego sumar los resultados.
- Si aplicas el operador a una función multiplicada por un número, es lo mismo que aplicar el operador a la función y luego multiplicar el resultado por ese número.
Estas propiedades hacen que los operadores lineales sean muy útiles para resolver ecuaciones diferenciales, que son ecuaciones que involucran funciones y sus derivadas.
Características de los Operadores Diferenciales
Los operadores diferenciales tienen varias características importantes:
- Son lineales: Como ya mencionamos, cumplen con las propiedades de linealidad. Esto es muy útil en matemáticas y física.
- Se pueden combinar: Puedes aplicar un operador diferencial y luego otro. Por ejemplo, si tienes un operador
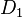 y otro
y otro 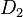 , puedes aplicar
, puedes aplicar 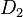 a una función y luego
a una función y luego 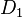 al resultado. Esto se escribe como
al resultado. Esto se escribe como 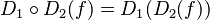 .
. - No siempre conmutan: A veces, el orden en que aplicas los operadores importa. Es decir, aplicar
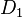 y luego
y luego 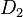 puede dar un resultado diferente a aplicar
puede dar un resultado diferente a aplicar 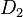 y luego
y luego 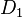 .
.
El Operador Del o Nabla
El operador diferencial "del", también conocido como nabla ( ), es muy importante en física y matemáticas. Se usa para describir cómo cambian las cosas en el espacio tridimensional.
), es muy importante en física y matemáticas. Se usa para describir cómo cambian las cosas en el espacio tridimensional.
En coordenadas cartesianas (x, y, z), se define como: 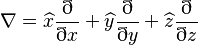
El operador nabla se usa para calcular:
- El gradiente de campos escalares (como la temperatura en una habitación, que tiene un valor en cada punto).
- La divergencia y el rotacional de campos vectoriales (como la dirección y fuerza del viento en diferentes puntos).
- El Laplaciano, que es otro operador importante en física.
Operadores con Varias Variables
Cuando las funciones dependen de varias variables (por ejemplo, la temperatura que depende de la posición x, y, z), usamos las derivadas parciales.
Derivadas Parciales
Las derivadas parciales nos dicen cómo cambia una función cuando solo una de sus variables cambia, manteniendo las otras constantes. Se escriben con el símbolo 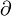 (una 'd' curvada):
(una 'd' curvada):
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\partial \over \partial x_i} o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \partial_i
Un operador muy conocido que usa derivadas parciales es el operador laplaciano (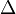 ), que se expresa como:
), que se expresa como: 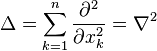 Este operador es fundamental en muchas áreas de la ciencia y la ingeniería.
Este operador es fundamental en muchas áreas de la ciencia y la ingeniería.
Cálculo Fraccional de Conjuntos
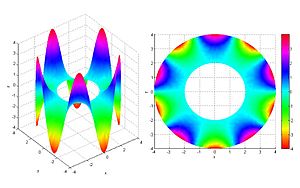
Existe una rama de las matemáticas llamada cálculo fraccional que estudia las derivadas e integrales de "orden no entero". Esto significa que, en lugar de tomar la primera o segunda derivada, podrías tomar una derivada de orden 0.5 o 1.3.
El Cálculo Fraccional de Conjuntos (FCS) es una forma de organizar y entender los muchos tipos de operadores fraccionales que existen. Se basa en la idea de que hay diferentes maneras de definir una derivada fraccional, y el FCS ayuda a clasificarlas.
La idea del cálculo fraccional surgió hace mucho tiempo, cuando el matemático L'Hopital le preguntó a Leibniz qué pasaría si se tomaba una derivada de orden 1/2. En ese momento, no había una respuesta clara, pero Leibniz predijo que algún día tendría usos importantes. Hoy en día, los operadores fraccionales se usan en campos como la física y la ingeniería para modelar sistemas complejos.
Véase también
 En inglés: Differential operator Facts for Kids
En inglés: Differential operator Facts for Kids
- Derivada
- Operador lineal
- Operador fraccional


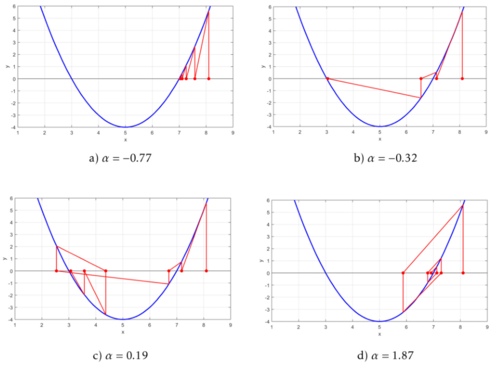
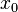 pero con diferentes órdenes
pero con diferentes órdenes  del operador fraccional implementado.
del operador fraccional implementado.