Centro de masas para niños
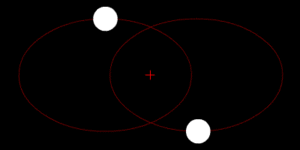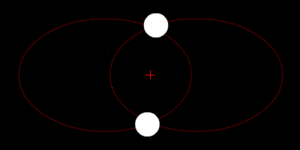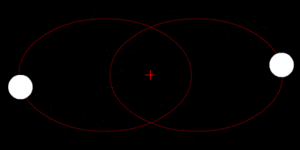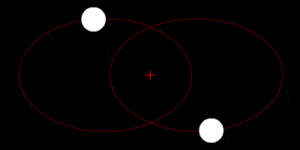
El centro de masas es un punto especial en un objeto o en un grupo de objetos. Imagina que es el lugar donde, si pudieras equilibrar todo el objeto o sistema, se mantendría perfectamente estable. Es como el punto de equilibrio de un objeto.
Este punto es muy importante en la física porque nos ayuda a entender cómo se mueven los objetos. Cuando estudiamos el movimiento de un objeto, a menudo podemos imaginar que toda su masa está concentrada en este único punto, lo que simplifica mucho los cálculos. Se abrevia como c.m.
Contenido
¿Cómo se relaciona el Centro de Masas con otros conceptos?
A veces, el centro de masas se confunde con otros conceptos como el centroide o el centro de gravedad. Aunque están relacionados, son diferentes:
- El centroide es un punto que solo depende de la forma de un objeto. No importa de qué material esté hecho o cómo esté distribuida su masa. Es un concepto puramente geométrico.
- El centro de gravedad es el punto donde parece que toda la fuerza de la gravedad actúa sobre un objeto. Depende de cómo está distribuida la masa y también de cómo es el campo gravitatorio (si la gravedad es igual en todas partes o no).
El centro de masas, el centroide y el centro de gravedad pueden coincidir en ciertas situaciones:
- El centro de masas es igual al centroide si el objeto tiene una densidad uniforme (es decir, el material está distribuido de manera igual por todo el objeto) o si tiene una forma muy simétrica.
- El centro de masas es igual al centro de gravedad si el objeto está en un campo gravitatorio uniforme, donde la fuerza de la gravedad es la misma en todas las direcciones y con la misma intensidad.
¿Cómo se calcula el Centro de Masas?
Calcular el centro de masas depende de si el objeto está formado por partes separadas o si es un objeto continuo.
Para objetos con partes separadas (distribución discreta)
Imagina que tienes varias pelotas pequeñas, cada una con su propia masa y posición. Para encontrar el centro de masas de este grupo de pelotas, usamos una fórmula que suma la masa de cada pelota multiplicada por su posición, y luego divide el resultado por la masa total de todas las pelotas.
La fórmula se ve así:
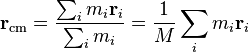
Donde:
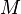 es la masa total de todas las pelotas juntas.
es la masa total de todas las pelotas juntas.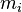 es la masa de cada pelota individual (la pelota "i").
es la masa de cada pelota individual (la pelota "i").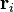 es la posición de cada pelota.
es la posición de cada pelota.
En palabras más sencillas, es como un promedio de las posiciones de todas las partes, pero dando más importancia a las partes que tienen más masa.
Para objetos continuos (distribución continua)
Cuando tienes un objeto que no está hecho de partes separadas, como una pelota de fútbol o un libro, su masa está distribuida de forma continua. Para calcular su centro de masas, necesitamos usar herramientas matemáticas más avanzadas, como las integrales.
La fórmula general es:
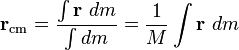
- Si la masa está distribuida de manera uniforme: Si el objeto tiene la misma densidad en todas sus partes (por ejemplo, una esfera de metal sólido y homogéneo), el centro de masas coincide con su centro geométrico (el centroide). La fórmula se simplifica:
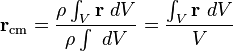
Aquí, V es el volumen total del objeto.
- Si la masa no está distribuida de manera uniforme: Si el objeto tiene partes más densas que otras (por ejemplo, una pelota con un peso en un lado), necesitamos conocer cómo varía la densidad en cada punto. La fórmula es:
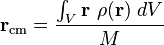
Donde 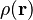 es la función que describe cómo cambia la densidad en el objeto.
es la función que describe cómo cambia la densidad en el objeto.
¿Para qué sirve el Centro de Masas?
El concepto de centro de masas es fundamental en muchas áreas de la física y la ingeniería:
- Movimiento de planetas: Los planetas y las estrellas orbitan alrededor de su centro de masas común, no solo alrededor del objeto más grande.
- Diseño de vehículos: Es crucial para la estabilidad de coches, aviones y barcos. Un centro de masas bajo ayuda a que un coche no se vuelque.
- Deportes: Los atletas, como los gimnastas o los saltadores de altura, manipulan su centro de masas para realizar movimientos complejos y mejorar su rendimiento.
- Robótica: Para que los robots puedan caminar o manipular objetos de forma estable, sus diseñadores deben calcular y controlar su centro de masas.
Para calcular el centro de masas de formas complejas, especialmente en objetos que giran, a veces se usa un teorema llamado teorema de Pappus-Guldin.
Ver también
Véase también
 En inglés: Center of mass Facts for Kids
En inglés: Center of mass Facts for Kids