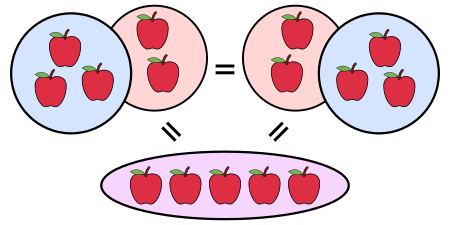
Conmutatividad para niños
En matemáticas, la propiedad conmutativa es una regla importante que tienen algunas operaciones. Significa que el resultado de una operación no cambia, aunque cambies el orden de los números o elementos que estás usando.
Piensa en la suma y la multiplicación. Si sumas 3 + 2, el resultado es 5. Si cambias el orden y sumas 2 + 3, el resultado sigue siendo 5. Lo mismo ocurre con la multiplicación: 2 x 3 es 6, y 3 x 2 también es 6. Por eso decimos que "el orden de los sumandos no altera la suma" y "el orden de los factores no altera el producto".
Esta idea de que el orden no importa en algunas operaciones se conoce desde hace mucho tiempo. Los matemáticos de la antigüedad ya la usaban, aunque no le dieron un nombre formal hasta el siglo XIX. A medida que se descubrieron más tipos de números (como los números negativos o las fracciones), la propiedad conmutativa siguió siendo válida para la suma y la multiplicación.
Sin embargo, no todas las operaciones son conmutativas. Por ejemplo, la resta y la división no lo son. Si restas 5 - 2, el resultado es 3, pero si restas 2 - 5, el resultado es -3. ¡Son diferentes!
La propiedad conmutativa es muy útil en matemáticas y en otras áreas, incluso en nuestra vida diaria.
Contenido
¿Qué significa la propiedad conmutativa?
La propiedad conmutativa se aplica a una operación que combina dos elementos. Si tienes dos elementos, digamos x e y, y una operación (que podemos llamar "estrella"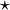 
), decimos que la operación es conmutativa si siempre se cumple que:
- x 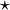y = y x
Esto significa que no importa si pones x primero y luego y, o si pones y primero y luego x; el resultado siempre será el mismo.
Ejemplos sencillos: Suma y multiplicación
La propiedad conmutativa es muy importante porque la suma y la multiplicación de números la cumplen.
Conmutatividad en la suma
Cuando sumas números, el orden no cambia el resultado. Por ejemplo:
- 2 + 3 = 5
- 3 + 2 = 5
En general, para cualquier par de números x e y:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + y = y + x
Conmutatividad en la multiplicación
Lo mismo ocurre con la multiplicación. El orden de los números no afecta el producto. Por ejemplo:
- 2
3 = 6 - 3 2 = 6
En general, para cualquier par de números x e y:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x \cdot y = y \cdot x
Esta propiedad se mantiene para diferentes tipos de números, como los números enteros (positivos y negativos), las fracciones y los números reales (todos los números que puedes imaginar en una línea).
Historia de la propiedad conmutativa
La idea de la conmutatividad se ha usado desde hace mucho tiempo.
Orígenes antiguos
Los egipcios ya usaban esta propiedad de la multiplicación para hacer sus cálculos más fáciles. En la Antigua Grecia, el famoso matemático Euclides también la consideró en sus escritos, como en su obra Elementos.
Nombramiento formal
El término "conmutativo" no se usó formalmente hasta principios del siglo XIX. Fue en 1814 cuando el matemático francés François Servois usó la expresión "conmutativas entre ellas" para describir funciones que se comportaban de esta manera. Más tarde, en 1841, Duncan Farquharson Gregory usó la frase "ley conmutativa" en inglés en un libro de cálculo.
Otros ejemplos de conmutatividad
En la lógica
La propiedad conmutativa también aparece en la lógica proposicional, que es una parte de la lógica que estudia cómo se combinan las afirmaciones. Por ejemplo, decir "P y Q" es lo mismo que decir "Q y P".
- (P y Q) es igual a (Q y P)
- (P o Q) es igual a (Q o P)
En la teoría de conjuntos
En la teoría de conjuntos, que estudia colecciones de elementos, la unión y la intersección de conjuntos son operaciones conmutativas.
- La unión de dos conjuntos A y B (A
B) es la misma que la unión de B y A (B A). - La intersección de dos conjuntos A y B (A
B) es la misma que la intersección de B y A (B A).
En la vida diaria
Puedes encontrar muchos ejemplos de la propiedad conmutativa en tu vida diaria:
- Ponerse los calcetines: No importa si te pones primero el calcetín derecho y luego el izquierdo, o al revés. El resultado final es el mismo: ¡tienes los dos calcetines puestos!
- Pagar con monedas: Si pagas algo con varias monedas, no importa el orden en que las entregues. El total de dinero que has pagado siempre será el mismo.
Ejemplos de operaciones no conmutativas
Es importante recordar que no todas las operaciones son conmutativas. Aquí tienes algunos ejemplos:
En matemáticas
- La resta: Como vimos antes, 5 - 2 no es lo mismo que 2 - 5.
- La división: 10 / 2 es 5, pero 2 / 10 es 0.2. Son resultados diferentes.
- La potenciación: 2 elevado a la 3 (23 = 8) no es lo mismo que 3 elevado a la 2 (32 = 9).
- La composición de funciones: Si tienes dos funciones, aplicar una y luego la otra puede dar un resultado diferente a aplicarlas en el orden inverso.
- La multiplicación de matrices: Las matrices son arreglos de números. Cuando las multiplicas, el orden sí importa.
En la vida diaria
También hay muchas acciones en la vida diaria que no son conmutativas:
- Lavar y planchar la ropa: Si lavas la ropa y luego la planchas, el resultado es ropa limpia y sin arrugas. Pero si planchas la ropa y luego la lavas, ¡el resultado es ropa arrugada y mojada! El orden importa.
- Concatenar textos: Si juntas las letras "C", "A", "S", "A", el resultado es "CASA". Pero si las juntas en otro orden, como "S", "A", "C", "A", el resultado es "SACA". El orden de las letras cambia la palabra.
- Movimientos del cubo de Rubik: Si haces un movimiento y luego otro en un cubo de Rubik, el resultado será diferente si haces esos mismos movimientos en el orden inverso.
Propiedades relacionadas
Asociatividad
La propiedad asociativa es otra regla importante en matemáticas. Dice que si tienes tres o más números con la misma operación, no importa cómo los agrupes (con paréntesis), el resultado será el mismo, siempre que el orden de los números no cambie. Por ejemplo, en la suma: (2 + 3) + 4 = 5 + 4 = 9. Y 2 + (3 + 4) = 2 + 7 = 9. La mayoría de las operaciones que son conmutativas también son asociativas, pero no siempre.
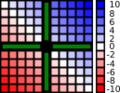
Simetría
La conmutatividad está relacionada con la simetría. Si una operación es conmutativa, puedes ver una especie de simetría en su representación. Por ejemplo, si dibujas un gráfico de la suma (como en la imagen de la derecha), verás que es simétrico.
Galería de imágenes
-
El primer uso conocido del término «conmutativo» fue en un artículo en francés, en 1814.
-
Gráfico que muestra la simetría de la función suma.
Véase también
En inglés: Commutative property Facts for Kids
