robot de la enciclopedia para niños

Momento de inercia para niños

Enciclopedia para niños

El momento de inercia (símbolo I) es una medida de lo difícil que es cambiar el movimiento de giro de un objeto. Imagina que quieres hacer girar algo o detener su giro; el momento de inercia te dice cuánta resistencia ofrece ese objeto a ese cambio.

Piensa en una bailarina de ballet: cuando gira con los brazos extendidos, gira más lento. Pero si los encoge y los pega al cuerpo, gira mucho más rápido. Esto sucede porque al extender los brazos, su masa se distribuye más lejos de su eje de giro, aumentando su momento de inercia. Al encogerlos, su masa está más cerca del eje, disminuyendo su momento de inercia y permitiéndole girar más rápido.

El momento de inercia nos muestra cómo está distribuida la masa de un objeto alrededor de un punto o línea por donde gira. Depende de la forma del objeto y de dónde esté el eje de giro, pero no de las fuerzas que lo hacen girar. Es como la masa en el movimiento en línea recta: la masa te dice qué tan difícil es mover un objeto en línea recta, y el momento de inercia te dice qué tan difícil es hacerlo girar.

¿Qué es el Momento de Inercia?

Cuando un objeto puede girar alrededor de un eje, necesitamos aplicar una fuerza de giro (llamada par o torque) para cambiar su cantidad de giro (su momento angular). La cantidad de fuerza de giro que se necesita para lograr una cierta aceleración de giro (qué tan rápido cambia su velocidad de giro) es proporcional al momento de inercia del objeto.

El momento de inercia se mide en unidades de kilogramo por metro cuadrado (kg·m²) en el Sistema Internacional de Unidades.

El momento de inercia es muy importante en el estudio del movimiento de giro, de la misma manera que la masa es importante en el estudio del movimiento en línea recta. Ambos nos dicen cuánto se resiste un cuerpo a cambiar su movimiento. El momento de inercia cambia si el eje de giro cambia, porque la distribución de la masa alrededor de ese eje también cambia.

Por ejemplo, para un punto de masa, el momento de inercia se calcula multiplicando la masa por el cuadrado de su distancia al eje de giro. Para un objeto más grande, es como sumar los momentos de inercia de todas sus pequeñas partes.

En 1673, Christiaan Huygens ya usaba una idea similar a esta al estudiar cómo oscilaban los objetos que colgaban y giraban, como un péndulo. El término "momento de inercia" fue introducido por Leonhard Euler en 1765.

El momento de inercia es clave para entender cómo se mueven los objetos que giran, como las ruedas de un coche o las aspas de un ventilador. Por ejemplo, el momento de inercia de un volante (una rueda pesada que gira) se usa en máquinas para mantener un giro suave, resistiendo los cambios en la fuerza de giro que se le aplica. También es fundamental para saber cómo un avión se mueve y gira en el aire.

¿Cómo se calcula el Momento de Inercia?

Para un sistema de partículas (muchos puntos pequeños de masa) y un eje de giro, el momento de inercia se calcula sumando el producto de la masa de cada partícula por el cuadrado de su distancia al eje.

Se expresa así: 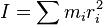I = \sum m_i r_i^2 \, Donde:

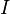  • I es el momento de inercia.
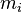  • m_i es la masa de cada pequeña parte del objeto.
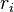  • r_i es la distancia de esa pequeña parte al eje de giro.

Para objetos que tienen una masa distribuida de forma continua (como una pelota o un cilindro), se usa una forma más avanzada de suma llamada integral, que considera todas las partes diminutas del objeto.

Este concepto es como la masa en la segunda ley de Newton para el movimiento en línea recta (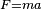\scriptstyle{F = m a}, donde la fuerza es igual a la masa por la aceleración). Para el movimiento de giro, la ley equivalente es: \tau = I \alpha\, Donde:

  • \scriptstyle{\tau} es la fuerza de giro (torque) aplicada al objeto.
  • \scriptstyle{I} es el momento de inercia del objeto respecto al eje de giro.
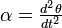  • \textstyle{\alpha={d^2\theta\over dt^2}} es la aceleración de giro (qué tan rápido cambia la velocidad de giro).

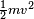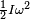La energía de movimiento de un objeto que gira también depende de su momento de inercia. Si un objeto se mueve en línea recta con velocidad v, su energía es \scriptstyle{{1\over 2}mv^2}. Si gira con velocidad de giro ω, su energía es \scriptstyle{{1\over 2}I\omega^2}.

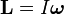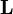La conservación del momento angular (la cantidad de giro de un objeto) también usa el momento de inercia: \mathbf{L} = I\boldsymbol{\omega} Donde \mathbf{L} es el momento angular e 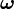\boldsymbol{\omega} es la velocidad de giro.

Teorema de Steiner: Un atajo para calcularlo

El Teorema de Steiner (nombrado así por Jakob Steiner) es una herramienta muy útil. Nos dice que si ya conoces el momento de inercia de un objeto respecto a un eje que pasa por su centro de masa (el punto donde se concentra toda su masa), puedes calcular fácilmente el momento de inercia respecto a cualquier otro eje que sea paralelo al primero.

La fórmula es: 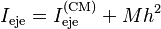I_{\rm eje} = I_{\rm eje}^{\rm (CM)} + Mh^2 \, Donde:

  • Ieje es el momento de inercia respecto al nuevo eje.
  • I(CM)eje es el momento de inercia respecto al eje que pasa por el centro de masa.
  • M es la masa total del objeto.
  • h es la distancia entre los dos ejes paralelos.

Este teorema es muy práctico porque a menudo es más fácil calcular el momento de inercia respecto al centro de masa, y luego usar esta fórmula para encontrarlo para cualquier otro eje paralelo.

Momentos de inercia de objetos simétricos

Aquí tienes algunos ejemplos de momentos de inercia para objetos comunes con masa distribuida de forma uniforme, cuando giran alrededor de un eje que pasa por su centro de masa:

Cuerpo Rígido Posición del eje de rotación Momento de Inercia (I)
Varilla delgada de longitud L y masa M CM 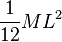\frac{1}{12}ML^2
Cono sólido de radio R (de la base) y masa M CM 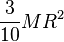\frac{3}{10}MR^2
Varilla delgada de longitud L y masa M Extremo de la varilla 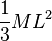\frac{1}{3}ML^2
Aro delgado de radio R y masa M CM 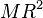MR^2
Cilindro sólido de radio R y masa M CM 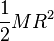\frac{1}{2}MR^2
Disco de radio R y masa M CM 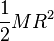\frac{1}{2}MR^2
Placa rectangular de lados a y b

con masa M

 CM 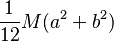\frac{1}{12}M(a^2+b^2)
Esfera sólida de radio R y masa M CM 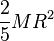\frac{2}{5}MR^2
Cascarón esférico de radio R y masa M CM 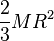\frac{2}{3}MR^2
Cilindro hueco de radios R1 y R2 con

masa M

 CM 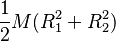\frac{1}{2}M(R_1^2+R_2^2)
Partícula de masa M a una distancia R

del eje de rotación

 Distancia R de la partícula 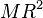MR^2

Galería de imágenes

  • Inertie balai

    ¿Cuál de estos giros resulta más difícil?
    El momento de inercia de un cuerpo indica su resistencia a adquirir una aceleración angular.

Véase también

Kids robot.svg En inglés: Moment of inertia Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Momento_de_inercia&oldid=4966497»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Momento de inercia para Niños. Enciclopedia Kiddle.