Sucesión (matemática) para niños

Enciclopedia para niños

Una sucesión en matemáticas es como una lista ordenada de números o de otros objetos. Imagina que tienes una fila de cosas donde el orden importa mucho. Por ejemplo, la lista de números (3, 5, 7, 9...) es una sucesión de números impares. Otro ejemplo es (2, 4, 8, 16...), que es una sucesión de las potencias de 2.

En una sucesión, cada elemento tiene una posición específica. Al primer elemento se le llama el primer término, al segundo el segundo término, y así sucesivamente. A diferencia de un grupo de objetos donde el orden no importa, en una sucesión sí es importante. Por ejemplo, la sucesión (A, B, C) es diferente de (C, A, B).

Las sucesiones pueden ser finitas, si tienen un número limitado de elementos (como la lista de letras (A, B, C)), o infinitas, si continúan sin fin (como los números pares: 2, 4, 6, 8...).

Contenido

Historia de las Sucesiones
Cómo se escriben las Sucesiones
Tipos de Sucesiones y sus Propiedades
Límites y Convergencia
- Sucesiones Convergentes
- Sucesiones de Cauchy
Generalización en distintas áreas
Galería de imágenes
Véase también

Historia de las Sucesiones

Las sucesiones que siguen una regla especial siempre han fascinado a los matemáticos. Aunque se conocían desde hace mucho tiempo, no se estudiaron a fondo hasta el siglo XVIII, cuando las matemáticas tuvieron un gran desarrollo. En esa época, se entendió mejor el concepto de "límite" de una sucesión, que es el valor al que se acercan sus términos.

Un matemático muy importante de esa época fue Leonhard Euler, quien hizo grandes aportaciones al estudio de las sucesiones. También es importante mencionar a Leonardo de Pisa, conocido como Fibonacci. En el siglo XII, él introdujo en Europa una de las sucesiones más famosas, los números de Fibonacci, que aparecen en muchos fenómenos de la naturaleza.

Las sucesiones se usan para organizar listas de elementos y son muy útiles en diferentes áreas, como la ciencia de la computación y la teoría de juegos.

Cómo se escriben las Sucesiones

Notación de las Sucesiones

Para escribir una sucesión, se usa una notación especial. Por ejemplo, se puede usar 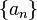$\{ a_n \}$ para representar una sucesión. Aquí, 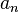$a_n$ es el elemento que está en la posición n. A este se le llama el término general. El pequeño número n (llamado subíndice) nos dice qué lugar ocupa el elemento en la sucesión.

Por ejemplo, para la sucesión de números pares positivos: 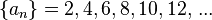$\{ a_n \}=2,4,6,8,10,12,\,...$

Esto significa que: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1 =2 (el primer término es 2) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_2=4 (el segundo término es 4) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_3=6 (el tercer término es 6) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_4=8 (el cuarto término es 8) ...y así sucesivamente.

Si los elementos de la sucesión siguen una regla, podemos escribir una fórmula para el término general. Para la sucesión de números pares, la fórmula es $a_n=2n$ . Así, si queremos saber el quinto término (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_5 ), solo tenemos que reemplazar n por 5: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_5 = 2 \times 5 = 10 .

A veces, las sucesiones empiezan con el término en la posición 0 (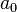 $a_0$ ) en lugar de la posición 1 ( 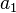$a_1$ ), especialmente en informática.

Sucesiones por Recurrencia

Algunas sucesiones se definen usando los términos anteriores. Esto se llama una relación de recurrencia. El ejemplo más famoso es la sucesión de Fibonacci. En esta sucesión, cada término (a partir del tercero) se obtiene sumando los dos términos anteriores.

La fórmula general para la sucesión de Fibonacci es: $a_n = a_{n-1} + a_{n-2}\,$

Esto significa que para encontrar el término 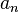$a_n$ , sumas el término anterior ( 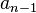$a_{n-1}$ ) y el término antes de ese ( 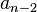$a_{n-2}$ ). Si los primeros dos términos son 1 y 1, la sucesión de Fibonacci sería: 1, 1, 2, 3, 5, 8, 13, ...

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_3 = a_2 + a_1 = 1 + 1 = 2
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_4 = a_3 + a_2 = 2 + 1 = 3
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_5 = a_4 + a_3 = 3 + 2 = 5

Las sucesiones por recurrencia son muy útiles para resolver problemas como calcular el interés compuesto o el número de movimientos en el juego de las Torres de Hanói.

Ejemplos Comunes de Sucesiones

Dos tipos de sucesiones muy comunes son las progresiones aritméticas y las progresiones geométricas.

Progresión Aritmética: En este tipo de sucesión, para pasar de un término al siguiente, siempre se suma la misma cantidad (una constante). Por ejemplo: 2, 5, 8, 11, ... (aquí se suma 3 cada vez).
Progresión Geométrica: Aquí, para pasar de un término al siguiente, siempre se multiplica por la misma cantidad (una constante). Por ejemplo: 3, 6, 12, 24, ... (aquí se multiplica por 2 cada vez).

Tipos de Sucesiones y sus Propiedades

Sucesiones Finitas e Infinitas

Como ya vimos, una sucesión puede tener un número limitado de elementos (finita) o un número ilimitado (infinita).

Una sucesión finita tiene una longitud específica. Por ejemplo, la sucesión de números primos menores que 10 es (2, 3, 5, 7). Su longitud es 4.
Una sucesión infinita continúa sin fin. Por ejemplo, la sucesión de todos los números naturales (1, 2, 3, 4, ...).

Subsucesiones

Una subsucesión es como una "sucesión dentro de otra sucesión". Se forma tomando algunos elementos de una sucesión original, pero manteniendo el orden en que aparecen. Por ejemplo, la sucesión de números pares (2, 4, 6, ...) es una subsucesión de los números naturales (1, 2, 3, 4, 5, 6, ...).

Sucesiones Monótonas

Una sucesión monótona es aquella en la que los términos siempre van en la misma dirección: o siempre crecen o siempre decrecen.

Sucesión Creciente: Cada término es igual o mayor que el anterior. Por ejemplo: 1, 3, 5, 7, ... o 2, 2, 4, 4, 6, 6, ...
Sucesión Estrictamente Creciente: Cada término es siempre mayor que el anterior. Por ejemplo: 1, 3, 5, 7, ...
Sucesión Decreciente: Cada término es igual o menor que el anterior. Por ejemplo: 10, 8, 6, 4, ... o 5, 5, 3, 3, 1, 1, ...
Sucesión Estrictamente Decreciente: Cada término es siempre menor que el anterior. Por ejemplo: 10, 8, 6, 4, ...

Ejemplo de una sucesión creciente
Ejemplo de una sucesión decreciente

Sucesiones Acotadas

Una sucesión está acotada si sus valores no se van al infinito, sino que se mantienen dentro de ciertos límites.

Acotada superiormente: Si hay un número M que es mayor o igual que todos los términos de la sucesión. Por ejemplo, en (1, 2, 3, 4, 5), el número 5 (o cualquier número mayor) la acota superiormente.
Acotada inferiormente: Si hay un número N que es menor o igual que todos los términos de la sucesión. Por ejemplo, en (1, 2, 3, 4, 5), el número 1 (o cualquier número menor) la acota inferiormente.
Acotada: Si está acotada tanto superior como inferiormente. Por ejemplo, la sucesión (1, 2, 3, 4, 5) está acotada.

Límites y Convergencia

Gráfica de una sucesión convergente {a_n} que se muestra en azul. Del gráfico se puede ver que la sucesión es convergente al límite cero cuando se incrementa n.

Sucesiones Convergentes

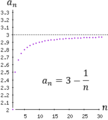
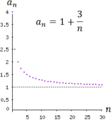
Una propiedad muy importante de las sucesiones es la convergencia. Si una sucesión converge, significa que sus términos se acercan cada vez más a un valor específico, llamado límite. Si una sucesión tiene un límite, decimos que es convergente. Si no tiene un límite, es divergente.

Imagina que los términos de la sucesión son como pasos que das. Si esos pasos te llevan cada vez más cerca de un punto fijo y te quedas muy, muy cerca de él, entonces la sucesión converge a ese punto.

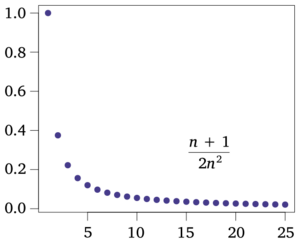
Por ejemplo, la sucesión (1/2, 1/3, 1/4, 1/5, ...) se acerca cada vez más a 0. Decimos que su límite es 0.

Las sucesiones oscilantes son un tipo de sucesiones divergentes. Sus términos suben y bajan sin acercarse a un solo valor. Un ejemplo es la sucesión (1, -1, 1, -1, ...), que alterna entre 1 y -1.

Sucesiones de Cauchy

Gráfica de una sucesión de Cauchy {x_n}.

Una sucesión de Cauchy es un tipo especial de sucesión donde los términos se acercan mucho entre sí a medida que avanzamos en la sucesión. No es que se acerquen a un límite específico, sino que la distancia entre ellos se hace cada vez más pequeña.

En el mundo de los números reales, si una sucesión es de Cauchy, ¡siempre es convergente! Esto es una propiedad muy útil en matemáticas.

Generalización en distintas áreas

Las sucesiones son herramientas muy versátiles y se usan en muchas ramas de las matemáticas y otras ciencias. Por ejemplo, un polinomio puede verse como una sucesión finita de números. También se usan en el estudio de matrices y en la ciencia de la computación.

Galería de imágenes

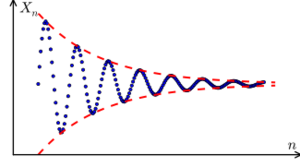
Una sucesión infinita de números reales (en azul). La sucesión no es ni creciente, ni decreciente, ni convergente, ni es una sucesión de Cauchy. Sin embargo, sí es una sucesión acotada.
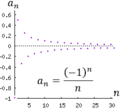
Ejemplo de una sucesión alternada.
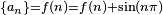Compruébese que $\scriptstyle \{ a_n^{}\} =f(n)=f(n)+\sin(n \pi)$ , ilustrando que dos funciones reales diferentes pueden corresponder a una misma sucesión sobre los enteros.

Véase también

En inglés: Sequence Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Sucesión_(matemática)&oldid=5005191»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Sucesión (matemática) para Niños. Enciclopedia Kiddle.