Espacio de Hilbert para niños

Enciclopedia para niños

En matemáticas, un espacio de Hilbert es un tipo especial de espacio que generaliza la idea de un espacio euclídeo. Piensa en el espacio euclídeo como el espacio de dos o tres dimensiones que usamos para dibujar o construir cosas. Los espacios de Hilbert extienden las herramientas del álgebra lineal y el cálculo que usamos en esos espacios a dimensiones mucho más grandes, ¡incluso infinitas!

Esto nos permite usar ideas geométricas como el ángulo entre "vectores" (que son como puntos o direcciones), la perpendicularidad, el teorema de Pitágoras, la proyección ortogonal (encontrar la parte de un vector que va en cierta dirección) y la distancia entre elementos. También nos ayuda a entender cómo las sucesiones de elementos se acercan a un punto.

Estos espacios llevan el nombre del matemático David Hilbert, quien los usó para estudiar ecuaciones integrales. Son muy importantes para entender las series de Fourier (que descomponen señales en ondas más simples) y son fundamentales en la mecánica cuántica, la rama de la física que estudia el mundo a escala muy pequeña.

Los espacios de Hilbert se estudian en una parte de las matemáticas llamada análisis funcional.

Contenido

¿Qué es un Espacio de Hilbert?
- ¿Para qué se usan los Espacios de Hilbert?
Ejemplos Sencillos de Espacios de Hilbert
Bases Ortonormales: Los "Ladrillos" del Espacio
- Dimensión de Hilbert
Operaciones con Espacios de Hilbert
- Suma Directa y Producto Tensorial
- Complementos y Proyecciones Ortogonales
Reflexividad
Operadores en Espacios de Hilbert
- Operadores Acotados
- Operadores No Acotados
Galería de imágenes
Véase también

¿Qué es un Espacio de Hilbert?

Para entender un espacio de Hilbert, primero necesitamos saber qué es un "producto interno" y una "norma".

Un producto interno es una operación que, en un espacio vectorial (que puede usar números reales o números complejos), nos permite "multiplicar" dos elementos para obtener un número. Este número nos da información sobre el ángulo y la longitud. Se escribe como <.,.>.

A partir de este producto interno, podemos definir una "norma" (||.||), que es como la longitud o el tamaño de un elemento. Se calcula así:

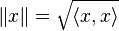
$\|x\| = \sqrt{\langle x,x \rangle}$

Un espacio vectorial H es un espacio de Hilbert si es "completo" con respecto a esta norma. Ser "completo" significa que no tiene "agujeros". Imagina una secuencia de puntos que se acercan cada vez más a un lugar; en un espacio completo, ese lugar al que se acercan siempre estará dentro del espacio.

Todos los espacios con producto interno que tienen un número finito de dimensiones (como el espacio euclídeo que conoces) son espacios de Hilbert. Esto es genial porque nos permite usar las ideas geométricas que ya conocemos en espacios con infinitas dimensiones.

¿Para qué se usan los Espacios de Hilbert?

Los espacios de Hilbert son herramientas muy poderosas en muchas áreas de la ciencia y la ingeniería. Aquí te mostramos algunos de sus usos más importantes:

Representaciones de grupos: Ayudan a entender cómo los grupos (conjuntos de elementos con una operación) pueden ser representados por transformaciones.
Procesos aleatorios: Se usan para estudiar procesos que cambian de forma impredecible, como el ruido en una señal.
Ecuaciones diferenciales: Son clave para resolver ecuaciones diferenciales parciales, que describen fenómenos como el calor, el sonido o la electricidad.
Análisis de señales: Permiten descomponer funciones complejas en partes más simples, como las wavelets, que son útiles para analizar imágenes o sonidos.
Mecánica cuántica: Son el lenguaje matemático principal para describir el comportamiento de las partículas subatómicas. En esta área, los elementos del espacio de Hilbert representan los posibles estados de un sistema físico.

Gracias al producto interno, podemos pensar en los espacios de Hilbert de una manera "geométrica", usando el lenguaje que ya conocemos de los espacios de pocas dimensiones. De todos los espacios vectoriales con infinitas dimensiones, los espacios de Hilbert son los que mejor se comportan y los más parecidos a los espacios de dimensión finita.

Los elementos de un espacio de Hilbert a veces se llaman "vectores", aunque en las aplicaciones suelen ser sucesiones de números complejos o funciones.

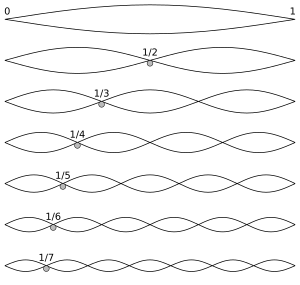
Una de las metas del análisis de Fourier es encontrar una forma de escribir una función como la suma (posiblemente infinita) de funciones más simples. Los espacios de Hilbert nos dan una forma abstracta de hacer esto: cada espacio de Hilbert tiene una base ortonormal, y cualquier elemento del espacio se puede escribir de forma única como una suma de múltiplos de estos elementos de la base.

Aunque David Hilbert los estudió, fue Hermann Weyl quien usó el término "espacio de Hilbert" en 1931, y John von Neumann fue quien más reconoció su importancia.

Ejemplos Sencillos de Espacios de Hilbert

Aquí veremos algunos ejemplos de espacios de Hilbert. Para simplificar, asumiremos que los números que usamos son números complejos, aunque las ideas son similares si usamos números reales.

Espacios Euclídeos (los que ya conoces)

El ejemplo más básico son los espacios de dimensión finita con el producto escalar normal. Por ejemplo, el espacio 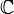$\mathbb{C}$ ⁿ (que es como el espacio 2D o 3D, pero con números complejos y más dimensiones) es un espacio de Hilbert con el siguiente producto interno:

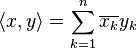
$\langle x, y \rangle = \sum_{k=1}^n \overline{x_k} y_k$

Aquí, la barra sobre un número complejo significa su "conjugado complejo", que es como su imagen en un espejo.

Espacios de Sucesiones

Los espacios de Hilbert no tienen por qué tener una dimensión finita; de hecho, muchos de los más útiles tienen infinitas dimensiones. Un ejemplo es el espacio 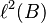$\ell^2(B)$ , que contiene sucesiones de números complejos. Una sucesión es una lista infinita de números. Para que una sucesión esté en este espacio, la suma de los cuadrados de los valores absolutos de sus elementos debe ser finita.

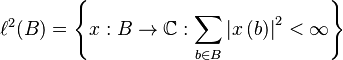
$\ell^2(B) =\left\{ x:B \rightarrow \mathbb{C}:\sum_{b \in B} \left|x \left(b\right)\right|^2 < \infty \right\}$

El producto interno para este espacio se define como:

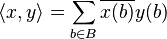
$\langle x, y \rangle = \sum_{b \in B} \overline{x(b)} y(b)$

Un ejemplo de una sucesión en 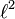$\ell^2$ (cuando B es el conjunto de números naturales) es:

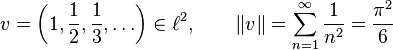
$v = \left(1, \frac{1}{2}, \frac{1}{3}, \dots \right)\in \ell^2, \qquad \|v\| = \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}$

Pero esta sucesión no está en 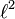$\ell^2$ :

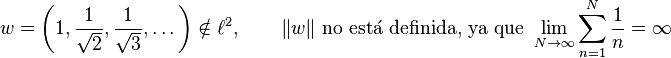
$w = \left(1, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{3}}, \dots \right)\notin \ell^2, \qquad \|w\|\text{ no está definida, ya que } \lim_{N\to \infty}\sum_{n=1}^N \frac{1}{n} = \infty$

Espacios de Funciones (Espacios de Lebesgue)

Otro ejemplo importante son los espacios L^p, que son espacios de funciones. Si p es igual a 2, estos espacios también son de Hilbert. El espacio L² _μ(X) contiene funciones que, al elevarlas al cuadrado y sumarlas (integrarlas), dan un resultado finito. El producto interno de dos funciones f y g en este espacio se calcula así:

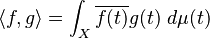
$\langle f,g\rangle=\int_X \overline{f(t)} g(t) \ d \mu(t)$

La integral de Lebesgue asegura que este espacio sea "completo".

Bases Ortonormales: Los "Ladrillos" del Espacio

Un concepto clave en los espacios de Hilbert es el de una base ortonormal. Piensa en ella como un conjunto de "ladrillos" especiales con los que puedes construir cualquier elemento del espacio. Una base ortonormal {e_k} cumple tres condiciones:

Normalizados: Cada "ladrillo" tiene una longitud de 1 (||e_k|| = 1).
Ortogonales: Cualquier par de "ladrillos" son perpendiculares entre sí (<e_k, e_j> = 0 si j ≠ k).
Expansión densa: Puedes combinar estos "ladrillos" para acercarte tanto como quieras a cualquier elemento del espacio.

Ejemplos de bases ortonormales:

En el espacio 3D normal (R³), el conjunto {(1,0,0), (0,1,0), (0,0,1)} es una base ortonormal.
Para el espacio de funciones L²([0, 1]), las funciones f_n(x) = exp(2πinx) forman una base ortonormal.

En los espacios de Hilbert de dimensión infinita, una base ortonormal no es una base en el sentido del álgebra lineal tradicional. Para distinguirlas, a la base tradicional se le llama "base de Hamel".

Se ha demostrado que cada espacio de Hilbert tiene al menos una base ortonormal, y todas las bases ortonormales de un mismo espacio tienen el mismo "tamaño" (el mismo número de elementos). Un espacio de Hilbert es "separable" si tiene una base ortonormal que se puede contar (como los números naturales).

Casi todos los espacios de Hilbert que se usan en la física son separables. Por eso, cuando los físicos hablan de "espacio de Hilbert", suelen referirse a un espacio separable.

Si {e_k} es una base ortonormal de un espacio H, entonces cualquier elemento x de H se puede escribir como una suma de los elementos de la base, multiplicados por ciertos números:

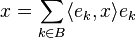
$x = \sum_{k \in B} \langle e_k , x \rangle e_k$

Esta suma se conoce como la expansión de Fourier de x.

Además, si tienes una base ortonormal, el espacio H es "isomorfo" a l²(B). Esto significa que son matemáticamente equivalentes, aunque se vean diferentes. Hay una función especial que transforma los elementos de H en elementos de l²(B) manteniendo sus propiedades de producto interno.

Dimensión de Hilbert

La "dimensión de Hilbert" de un espacio es el número de elementos que tiene cualquiera de sus bases ortonormales. Se escribe así:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \dim_{Hil} \mathcal{H} = \# \mathcal{B}_\mathcal{H}

Esta dimensión puede ser diferente de la dimensión "normal" (dimensión de Hamel) de un espacio vectorial. De hecho, la dimensión de Hilbert siempre es menor o igual que la dimensión de Hamel. En el caso de dimensiones finitas, son iguales.

Operaciones con Espacios de Hilbert

Suma Directa y Producto Tensorial

Podemos combinar dos o más espacios de Hilbert para crear uno más grande.

La suma directa (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): H_1 \oplus H_2 ) es como juntar los dos espacios sin que se superpongan, creando un espacio donde la dimensión es la suma de las dimensiones individuales.

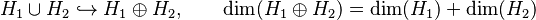
$H_1 \cup H_2 \hookrightarrow H_1 \oplus H_2, \qquad \mbox{dim}(H_1 \oplus H_2) = \mbox{dim}(H_1) + \mbox{dim}(H_2)$

El producto tensorial (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): H_1 \otimes H_2 ) es una forma más compleja de combinarlos, donde la dimensión del nuevo espacio es el producto de las dimensiones individuales.

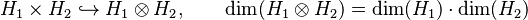
$H_1 \times H_2 \hookrightarrow H_1 \otimes H_2, \qquad \mbox{dim}(H_1 \otimes H_2) = \mbox{dim}(H_1) \cdot \mbox{dim}(H_2)$

Complementos y Proyecciones Ortogonales

Si tenemos un subconjunto S dentro de un espacio de Hilbert H, podemos definir el conjunto de todos los vectores que son perpendiculares a cada elemento de S. A este conjunto se le llama 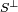$\scriptstyle S^\bot$ (se lee "S-perp"):

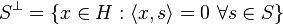
$S^\bot = \left\{ x \in H : \langle x, s \rangle = 0\ \forall s \in S \right\}$

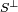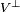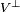$\scriptstyle S^\bot$ es también un espacio de Hilbert. Si V es un subespacio cerrado de H, entonces $\scriptstyle V^\bot$ es su "complemento ortogonal". Esto significa que cualquier elemento x en H se puede escribir de forma única como la suma de un elemento de V y un elemento de $\scriptstyle V^\bot$ .

El operador P_V que toma un elemento x y lo convierte en su parte v (la que está en V) se llama la proyección ortogonal sobre V. Piensa en ello como la "sombra" de x sobre el subespacio V. Esta proyección es el elemento de V que está más cerca de x.

Reflexividad

Una propiedad importante de los espacios de Hilbert es su "reflexividad". Esto significa que el espacio "dual" (el espacio de todas las funciones lineales continuas que van del espacio a los números) es muy parecido al espacio original. De hecho, el teorema de representación de Riesz nos dice que para cada función en el espacio dual, hay un único elemento en el espacio de Hilbert original que la representa. Esta conexión es muy útil en física, especialmente en la notación bra-ket de la mecánica cuántica.

Operadores en Espacios de Hilbert

Los "operadores" son como funciones que transforman elementos de un espacio de Hilbert en otros elementos del mismo espacio.

Operadores Acotados

Los operadores lineales "continuos" A: H → H son de especial interés. Un operador continuo es "acotado", lo que significa que no "estira" los elementos de forma infinita. Podemos definir su "norma" (su "tamaño" máximo) así:

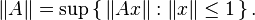
$\lVert A \rVert = \sup \left\{\,\lVert Ax \rVert : \lVert x \rVert \leq 1\,\right\}.$

La suma y la composición de operadores continuos también son continuas. Para cada operador A, existe otro operador llamado su "adjunto" (A^*), que cumple una relación especial con el producto interno.

El conjunto de todos los operadores lineales continuos en H forma una estructura matemática llamada C^*-álgebra.

Un operador A se llama "auto-adjunto" o "hermitiano" si A^* = A. Estos operadores se parecen mucho a los números reales y son muy importantes en física.

Un operador U se llama "unitario" si es "reversible" y su inverso es igual a su adjunto (U^*). Los operadores unitarios conservan el producto interno, es decir, no cambian las longitudes ni los ángulos.

Operadores No Acotados

En mecánica cuántica, también se usan operadores lineales que no son necesariamente continuos ni están definidos en todo el espacio H. Solo se requiere que estén definidos en una parte "densa" del espacio (una parte que está "cerca" de todos los puntos del espacio). Es posible definir operadores no acotados auto-adjuntos, y estos representan las "observables" (cosas que se pueden medir) en la mecánica cuántica.

Ejemplos de operadores no acotados auto-adjuntos en el espacio de Hilbert L²(R) (un espacio de funciones):

El operador diferencial:

$[A f](x) = - i \frac{d}{dx} f(x), \quad$

donde i es la unidad imaginaria. Este operador se relaciona con el "momento" (cantidad de movimiento) de una partícula.

El operador de multiplicación por x:

$[B f] (x) = xf(x).\quad$

Este operador se relaciona con la "posición" de una partícula.

Estos operadores no están definidos para todas las funciones, pero sí para un conjunto muy grande de ellas.

Los espacios de Hilbert se pueden utilizar para estudiar los armónicos de cuerdas vibrantes.

Galería de imágenes

Los espacios de Hilbert se pueden utilizar para estudiar los armónicos de cuerdas vibrantes.

Véase también

En inglés: Hilbert space Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Espacio_de_Hilbert&oldid=4747329»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Espacio de Hilbert para Niños. Enciclopedia Kiddle.