Orbital atómico para niños
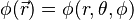 son funciones de tres variables (la distancia al núcleo, r, y los dos ángulos,
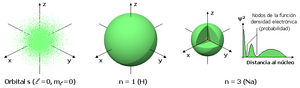
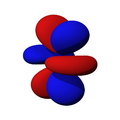
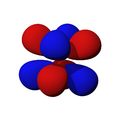
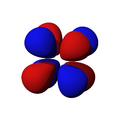
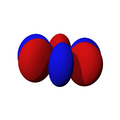
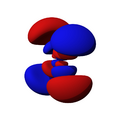
son funciones de tres variables (la distancia al núcleo, r, y los dos ángulos, 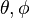 ). Las imágenes mostradas representan únicamente la componente angular de cada orbital que define su forma. El cambio de color en la escala de grises indica un cambio de signo en el OA y, según el caso, evidencia la presencia de superficies nodales, donde la función de onda se anula.
). Las imágenes mostradas representan únicamente la componente angular de cada orbital que define su forma. El cambio de color en la escala de grises indica un cambio de signo en el OA y, según el caso, evidencia la presencia de superficies nodales, donde la función de onda se anula.Un orbital atómico (OA) es una descripción matemática que nos ayuda a entender dónde es más probable encontrar un solo electrón dentro de un átomo. Imagina que no podemos saber exactamente dónde está un electrón en un momento dado, pero sí podemos saber en qué región del espacio es más probable que se encuentre. Esa región es lo que llamamos un orbital atómico.
Este concepto viene de la Mecánica cuántica, una rama de la física que estudia el comportamiento de las partículas muy pequeñas, como los electrones. Los orbitales atómicos son como las "casas" o "espacios" que los electrones pueden ocupar alrededor del núcleo atómico.
Cada orbital atómico se define por tres números especiales, llamados números cuánticos. Estos números nos dicen la energía del electrón, la forma del orbital y cómo se orienta en el espacio.
La idea de un orbital atómico nos permite calcular la probabilidad de encontrar un electrón en un lugar específico del átomo. Si juntamos todas las probabilidades de todos los electrones, podemos entender cómo se distribuyen alrededor del núcleo, formando lo que se conoce como la corteza electrónica o las capas electrónicas de un átomo.
Contenido
¿Qué es un Orbital Atómico?
El orbital atómico 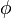 nos da toda la información sobre cómo se mueve un electrón en el espacio dentro de un átomo. Esta información está definida por los tres números cuánticos
nos da toda la información sobre cómo se mueve un electrón en el espacio dentro de un átomo. Esta información está definida por los tres números cuánticos  ,
,  y
y 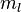 .
.
Gracias a la mecánica cuántica, que describe a los electrones como ondas, podemos definir el tamaño, la forma y la orientación de la región del espacio donde un electrón puede estar. Cada orbital con un valor diferente de n tiene una energía específica para el electrón.
La probabilidad de encontrar un electrón en un punto del espacio se describe usando sus coordenadas. En los átomos, que suelen tener una forma esférica, usamos coordenadas especiales para describir esta probabilidad.
Descubriendo los Fundamentos Físicos de los Orbitales
La Función de Onda y la Ecuación de Schrödinger
En el modelo atómico moderno, que surgió después de otros como el modelo atómico de Bohr, los orbitales atómicos son funciones que describen cómo se comportan los electrones en un átomo. Son como "estados" estables que un electrón puede tener.
Estas funciones se obtienen al resolver una ecuación muy importante llamada ecuación de Schrödinger. Esta ecuación nos ayuda a entender dónde es más probable encontrar un electrón alrededor del núcleo. No nos dice la posición exacta del electrón, porque en el mundo cuántico no podemos saberlo con total precisión. En cambio, nos da una región del espacio donde la probabilidad de encontrar al electrón es muy alta.
Los Números Cuánticos: Las Claves de los Electrones
Para el átomo de hidrógeno, que es el más simple, la ecuación de Schrödinger se puede resolver de forma exacta. Las soluciones de esta ecuación nos muestran que las funciones de onda de los electrones están determinadas por tres números cuánticos:  ,
,  y
y 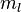 . Estos números surgen de las reglas que rigen el movimiento de los electrones dentro del átomo. No todos los estados y energías son posibles.
. Estos números surgen de las reglas que rigen el movimiento de los electrones dentro del átomo. No todos los estados y energías son posibles.
Veamos qué significan estos números:
- Número cuántico principal (n): Este número (1, 2, 3...) define el nivel de energía total del electrón y el tamaño del orbital. Cuanto mayor sea n, más grande será el orbital y mayor la energía del electrón. Si
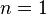 , el electrón está en su estado de energía más baja, que es el más estable.
, el electrón está en su estado de energía más baja, que es el más estable. - Número cuántico azimutal (l): Este número (0, 1, 2... hasta n-1) define la forma del orbital y el "giro" del electrón alrededor del núcleo (su momento angular). Para cada valor de
 , los orbitales tienen un nombre especial:
, los orbitales tienen un nombre especial:
- Si
 = 0, son orbitales s (esféricos).
= 0, son orbitales s (esféricos). - Si
 = 1, son orbitales p (con forma de dos lóbulos).
= 1, son orbitales p (con forma de dos lóbulos). - Si
 = 2, son orbitales d (con formas más complejas).
= 2, son orbitales d (con formas más complejas). - Si
 = 3, son orbitales f (aún más complejas).
= 3, son orbitales f (aún más complejas). - Si
 = 4, son orbitales g, y así sucesivamente siguiendo el orden alfabético.
= 4, son orbitales g, y así sucesivamente siguiendo el orden alfabético.
- Si
- Número cuántico magnético (ml): Este número (0, ±1, ±2... hasta ±
 ) define la orientación del orbital en el espacio, especialmente cuando hay un campo magnético externo.
) define la orientación del orbital en el espacio, especialmente cuando hay un campo magnético externo.
Además de estos tres, se añadió un cuarto número cuántico, 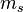 , para describir completamente el estado de un electrón. Este número se refiere al "espín" del electrón, que es como si el electrón girara sobre su propio eje. El espín puede tener dos valores: +1/2 o -1/2.
, para describir completamente el estado de un electrón. Este número se refiere al "espín" del electrón, que es como si el electrón girara sobre su propio eje. El espín puede tener dos valores: +1/2 o -1/2.
Un orbital atómico se puede dividir en dos partes: una que depende de la distancia al núcleo (parte radial) y otra que depende de los ángulos (parte angular). La parte angular es la que le da la forma característica a cada orbital.
Más Allá del Átomo de Hidrógeno: Átomos con Muchos Electrones
Los orbitales atómicos son ideales para describir el átomo de hidrógeno porque solo tiene un electrón. Pero, ¿qué pasa con los átomos que tienen muchos electrones?
En átomos con más de un electrón, los electrones se repelen entre sí. Esto hace que la ecuación de Schrödinger sea mucho más difícil de resolver de forma exacta. Por eso, para estos átomos, usamos los orbitales atómicos como una buena aproximación. Imaginamos que cada electrón se mueve bajo la influencia del núcleo y de un "campo promedio" creado por los otros electrones.
Aunque es una aproximación, los orbitales atómicos son increíblemente útiles en la química para entender cómo se comportan los electrones no solo en los átomos con muchos electrones, sino también en las moléculas. Los químicos a menudo dicen que "en un orbital caben dos electrones", lo que es una forma sencilla de recordar una de las reglas básicas de cómo se llenan los orbitales.
Las Formas de los Orbitales Atómicos
Podemos representar en 3D la forma de los orbitales atómicos. Estas imágenes nos muestran la región donde es más probable encontrar un electrón. A veces, las imágenes solo muestran la parte angular, que es la que define la forma.
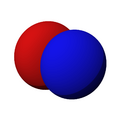
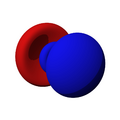
Orbitales s
Los orbitales "s" tienen una forma de esfera alrededor del núcleo atómico. La probabilidad de encontrar el electrón es mayor cerca del centro y disminuye a medida que nos alejamos.
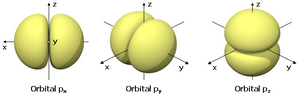
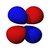
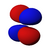
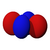
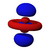
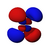
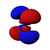
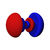
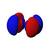
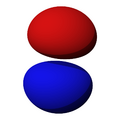
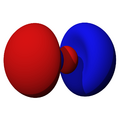
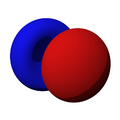
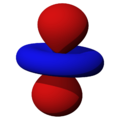
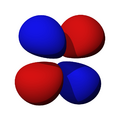
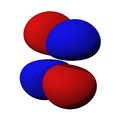
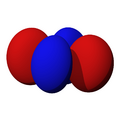
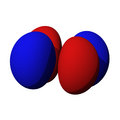
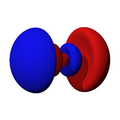
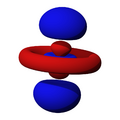
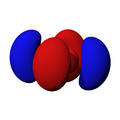
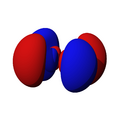
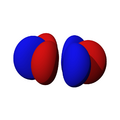
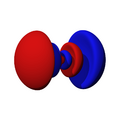
Orbitales p
Los orbitales "p" tienen una forma como de dos esferas unidas por el centro (el núcleo), orientadas a lo largo de los ejes X, Y o Z. Hay tres orbitales "p" diferentes, cada uno apuntando en una dirección. A medida que el número cuántico principal aumenta, la probabilidad de encontrar el electrón se aleja más del núcleo.
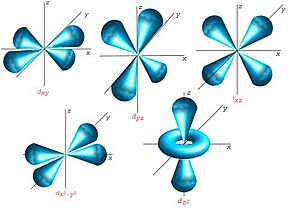
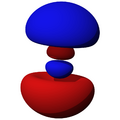
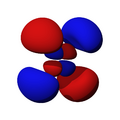
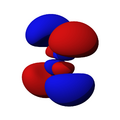
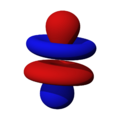
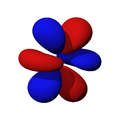
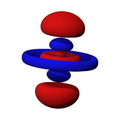
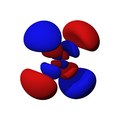
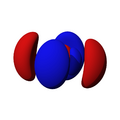
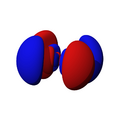
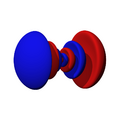
Orbitales d
Los orbitales "d" tienen formas más variadas y complejas. Cuatro de ellos parecen tréboles de cuatro hojas, y el quinto tiene forma de dos lóbulos con un anillo alrededor. Hay cinco orbitales "d" diferentes.
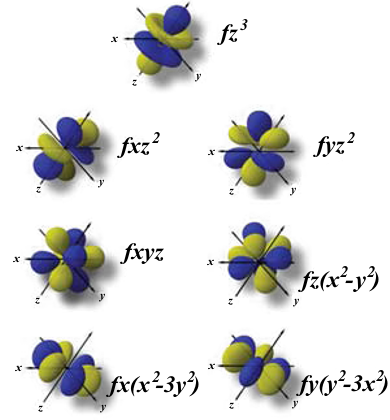
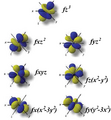
Orbitales f
Los orbitales "f" tienen formas aún más complejas y exóticas. Hay siete orbitales "f" diferentes.
Orbitales g
Los orbitales "g" son teóricos para elementos con muchos electrones. Tendrían formas aún más complicadas.
Tabla de Orbitales
La siguiente tabla muestra las formas de los orbitales para el átomo de hidrógeno, desde el 1s hasta el 8s. En átomos con muchos electrones, estos se van acomodando en estos grupos de orbitales.
Galería de imágenes
-
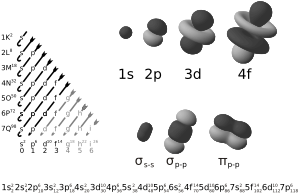
Representaciones 3D de Orbitales atómicos (arriba a la derecha) y moleculares (abajo a la derecha). A la izquierda se muestra el Diagrama de Moeller, gráfica mnemotécnica que ayuda a seguir la regla de Madelung a fin de construir la configuración electrónica (orden de llenado y ocupación de los orbitales, mostrado al pie de la figura) a partir del conocimiento del número atómico Z, siguiendo el Principio de Aufbau. Nota: se debe tener en cuenta que los orbitales atómicos
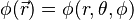 son funciones de tres variables (la distancia al núcleo, r, y los dos ángulos,
son funciones de tres variables (la distancia al núcleo, r, y los dos ángulos, 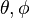 ). Las imágenes mostradas representan únicamente la componente angular de cada orbital que define su forma. El cambio de color en la escala de grises indica un cambio de signo en el OA y, según el caso, evidencia la presencia de superficies nodales, donde la función de onda se anula.
). Las imágenes mostradas representan únicamente la componente angular de cada orbital que define su forma. El cambio de color en la escala de grises indica un cambio de signo en el OA y, según el caso, evidencia la presencia de superficies nodales, donde la función de onda se anula.
Véase también
 En inglés: Atomic orbital Facts for Kids
En inglés: Atomic orbital Facts for Kids
- Mecánica cuántica
- Química cuántica
- Configuración electrónica
- Orbital molecular