Norma vectorial para niños
Una norma es como una regla especial que nos permite medir el "tamaño" o la "longitud" de un vector en matemáticas y física. Imagina que un vector es una flecha que apunta en una dirección y tiene un cierto largo. La norma nos dice qué tan larga es esa flecha.
No todos los vectores son iguales, y no siempre se miden de la misma manera. Por eso, existen diferentes tipos de normas, pero todas deben cumplir ciertas reglas para ser consideradas una "norma".
La norma más conocida es la norma euclídea, que es la forma en que medimos las distancias en el mundo real, como la distancia en línea recta entre dos puntos. Pero en el mundo de las matemáticas, un mismo espacio de vectores puede tener varias formas de medir su longitud.
Cada norma nos ayuda a entender mejor cómo se comportan los vectores y cómo se relacionan entre sí.
Plantilla:Ficha de concepto matemático
Contenido
¿Qué es la Norma Euclídea?
La norma euclídea es la forma más común y fácil de entender para medir la longitud de un vector. Piensa en ella como la distancia en línea recta que hay desde el punto de inicio de un vector hasta su punto final. Es como usar una cinta métrica para saber cuánto mide algo.
Norma Euclídea en dos dimensiones
Si tienes un vector en un plano (como un dibujo en una hoja de papel), puedes usar sus coordenadas para calcular su longitud. Imagina que el vector va del punto A al punto B. Si el punto A está en (a1, a2) y el punto B en (b1, b2), la longitud del vector se calcula así: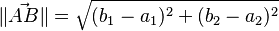 
Esto es muy parecido al Teorema de Pitágoras, que usas para calcular la hipotenusa de un triángulo rectángulo.
Norma Euclídea en tres dimensiones
Si el vector está en un espacio tridimensional (como el mundo real, con alto, ancho y profundidad), la fórmula es similar, pero con una coordenada más: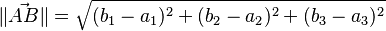 
Aquí, el punto A está en (a1, a2, a3) y el punto B en (b1, b2, b3).
Norma Euclídea en general
Para cualquier número de dimensiones, la idea es la misma: sumas los cuadrados de las diferencias de las coordenadas y luego sacas la raíz cuadrada. Si un vector tiene componentes (v1, v2, ..., vn), su norma euclídea es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \|\mathbf{v}\| = \sqrt{v_1^2+v_2^2+\cdots+v_n^2}
Reglas para cualquier Norma
Para que una forma de medir la longitud de un vector sea considerada una "norma", debe cumplir tres reglas importantes. Estas reglas aseguran que la medida sea lógica y útil:
- Siempre es positiva (o cero): La longitud de un vector nunca puede ser un número negativo. Solo es cero si el vector es el "vector nulo", que es como un punto sin longitud ni dirección.
- Cambia de tamaño proporcionalmente: Si multiplicas un vector por un número (por ejemplo, lo haces el doble de largo), su norma también se multiplicará por ese número. Si un vector mide 5 unidades y lo multiplicas por 2, ahora medirá 10 unidades.
- La regla del triángulo: Imagina que tienes dos vectores que, al sumarse, forman un tercer vector. La longitud del vector resultante siempre será igual o menor que la suma de las longitudes de los dos vectores originales. Piensa en un triángulo: la suma de las longitudes de dos lados siempre es mayor o igual que la longitud del tercer lado.
Cuando un espacio vectorial tiene una norma definida, se le llama espacio normado.
Ejemplos de otras Normas
Además de la norma euclídea, existen otras formas de medir la longitud de un vector. Aquí te mostramos algunas:
- Norma-p: Esta es una forma general de calcular la norma. La norma euclídea es un caso especial de la norma-p, cuando p es igual a 2. Si p es igual a 1, se llama norma del taxista, porque es como la distancia que recorrería un taxi en una ciudad con calles en cuadrícula (solo puede ir en horizontal o vertical, no en diagonal).
- Norma infinito: Esta norma mide la longitud de un vector tomando el valor absoluto más grande de sus componentes. Por ejemplo, si un vector es (3, -5, 2), su norma infinito sería 5 (porque es el valor absoluto más grande).
Distancia que crea una Norma
Cualquier norma que definamos en un espacio de vectores nos permite también calcular la distancia entre dos vectores. Simplemente restamos un vector del otro y luego calculamos la norma del resultado. Esto nos ayuda a saber qué tan "cerca" o "lejos" están los vectores entre sí.
Gracias a las normas, podemos entender conceptos como la "cercanía" y los "límites" en el mundo de las matemáticas, lo cual es muy importante para muchas áreas de la ciencia y la ingeniería.
Véase también
En inglés: Norm (mathematics) Facts for Kids
