robot de la enciclopedia para niños

Matriz transpuesta para niños

Enciclopedia para niños
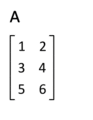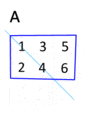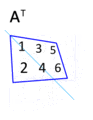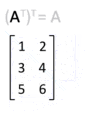
Archivo:Matrix transpose
La traspuesta AT de una matriz A puede ser obtenida reflejando los elementos a lo largo de su diagonal. Repitiendo el proceso en la matriz traspuesta devuelve los elementos a su posición original. Así, la traspuesta de una traspuesta es la matriz original, (AT)T = A.

Sea A una matriz con m filas y n columnas. La matriz traspuesta, denotada con A^t.

Está dada por:

(A^t)_{ij} = A_{ji},\ 1\le i\le n,\ 1\le j\le m

En donde el elemento a_{ji} de la matriz original A se convertirá en el elemento a_{ij} de la matriz traspuesta A^t.

Ejemplos

\begin{bmatrix} a & b \\ c & d \\ e & f \\ \end{bmatrix}^t = \begin{bmatrix} a & c & e \\ b & d & f \\ \end{bmatrix}
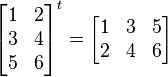
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix}^t = \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}

Otro ejemplo un poco más grande es el siguiente:

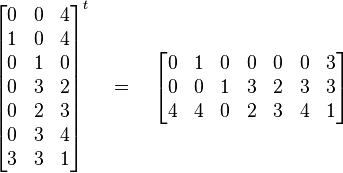
\begin{bmatrix} 0 & 0 & 4 \\ 1 & 0 & 4 \\ 0 & 1 & 0 \\ 0 & 3 & 2 \\ 0 & 2 & 3 \\ 0 & 3 & 4 \\ 3 & 3 & 1 \end{bmatrix}^t \quad = \quad \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 3 \\ 0 & 0 & 1 & 3 & 2 & 3 & 3 \\ 4 & 4 & 0 & 2 & 3 & 4 & 1 \end{bmatrix}

Propiedades

  • Para toda matriz A,
(A^t)^t = A \,
Demostración
Se recurre a la definición de trasposición elemento a elemento, sean aij dichos elementos, denotando por A = (aij)ij a la matriz, se tiene

(A^t)^t = \left( \left(a_{ij}\right)_{ij}^t \right)^t=\left( \left(a_{ji}\right)_{ij} \right)^t=\left(a_{ij}\right)_{ij}=A ∎
  • Sean A y B matrices con elementos en un anillo \mathcal{A} y sea c \in \mathcal{A} :
(A + B)^t = A^t + B^t \,
Demostración
Denotando por A = (aij)ij, B = (bij)ij y A+B = (cij)ij, donde cij = aij+bij, se tiene

(A+B)^t = \left(c_{ij}\right)_{ij}^t = \left(c_{ji}\right)_{ij} = \left(a_{ji}+b_{ji}\right)_{ij} = \left(a_{ji}\right)_{ij} + \left(b_{ji}\right)_{ij} = A^t + B^t ∎
(c \, A)^t = c \, A^t
Demostración
Se recurre a la definición de producto por escalar como operación externa

c A = c \left(a_{ij}\right)_{ij} = \left( c a_{ij}\right)_{ij}

sea dij = c aij, con esta notación se tiene c A = (dij)ij, por trasposición queda

(c A)^t = \left(d_{ij}\right)_{ij}^t = \left( d_{ji}\right)_{ij} = \left( c a_{ji}\right)_{ij} = c A^t ∎
  • Para el producto usual de las matrices A y B,
(AB)^t = B^tA^t \,
Demostración
Se recurre a la definición de producto matricial, sean A = (aij)ij, B = (bij)ij y A B = (cij)ij entonces por definición

c_{ij}=\sum_{k=1}^r a_{ik}b_{kj}

por trasposición queda

c_{ji}=\sum_{k=1}^r a_{jk}b_{ki}=\sum_{k=1}^r b_{ki}a_{jk}

que coincide con la definición de producto para Bt At∎
  • Si A es una matriz cuadrada cuyas entradas son números reales, entonces
A^t A \,

es semidefinida positiva.

Demostración
Sean A una matriz de tamaño m × n y x un vector columna de n componentes perteneciente a un espacio normado, con \scriptstyle\|\cdot\| denotando la norma euclídea.

x^t A^t A x = (A x)^t A x = \| A x \|^2

de las propiedades de la norma se deduce xt At A x ≥ 0 para todo x, luego At A es semidefinida positiva. ∎

Definiciones asociadas

Una matriz cuadrada A es simétrica si coincide con su traspuesta:

A^t = A \,

Una matriz cuadrada A es antisimétrica si su traspuesta coincide con su inverso aditivo.

A^t = -A \,

Si los elementos de la matriz A son números complejos y su traspuesta coincide con su conjugada, se dice que la matriz es hermítica.

A^t = \bar{A}, \quad A = (\bar{A})^t = A^\dagger

y antihermítica si

A^t = -\bar{A}

Vale la pena observar que si una matriz es hermítica (matriz simétrica en el caso de matriz real) entonces es diagonalizable y sus autovalores son reales. (El recíproco es falso).

Véase también

Kids robot.svg En inglés: Transpose Facts for Kids

  • La definición de matriz traspuesta se usa en la definición de Matriz ortogonal.
  • Escítala : Instrumento antiguo para cifrar mensajes basado en la trasposición de matrices.

de:Matrix (Mathematik)#Die transponierte Matrix

Obtenido de «https://ninos.kiddle.co/index.php?title=Matriz_transpuesta&oldid=3779702»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Matriz transpuesta para Niños. Enciclopedia Kiddle.