Matriz invertible para niños

En matemáticas, especialmente en el álgebra lineal, una matriz cuadrada es como una tabla de números organizada en filas y columnas, donde el número de filas es igual al número de columnas. Una matriz cuadrada, por ejemplo, una de 3x3 (3 filas y 3 columnas), se llama invertible (o también no singular o regular) si existe otra matriz especial que, al multiplicarla por la primera, da como resultado una matriz identidad. La matriz identidad es como el número 1 en la multiplicación normal: no cambia nada. Se representa con la letra I. Si una matriz no es invertible, se le llama singular o degenerada.

Una matriz es singular si su determinante es cero. El determinante es un número especial que se calcula a partir de los elementos de la matriz y nos da información importante sobre ella. El proceso de encontrar la matriz inversa se llama inversión de matrices.

¿Qué es una Matriz Inversa?

Una matriz inversa de una matriz A se escribe como A^-1. Si multiplicamos A por A^-1 (en cualquier orden), el resultado siempre será la matriz identidad (I). Esto es similar a cómo 5 multiplicado por 1/5 (su inverso) es igual a 1.

¿Cómo se calcula la inversa de una matriz 2x2?

Para una matriz pequeña de 2x2, calcular su inversa es más sencillo. Imagina que tienes una matriz A con estos números: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} Su determinante se calcula como ad - bc. Si este número no es cero, la matriz tiene inversa. La fórmula para encontrar su inversa es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A^{-1}= \frac{1}{ad - bc} \begin{bmatrix} \,\,\,d & \!\!-b \\ -c & \,a \\ \end{bmatrix}

Por ejemplo, si tenemos la matriz: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{bmatrix} 2 & 1 \\ 5 & 3 \end{bmatrix} Primero calculamos su determinante: (2 * 3) - (1 * 5) = 6 - 5 = 1. Como el determinante es 1 (no cero), la matriz es invertible. Ahora aplicamos la fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{1} \begin{bmatrix} \,\,\,3 & \!\!-1 \\ -5 & \,2 \\ \end{bmatrix} = \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix} Si multiplicamos la matriz original por su inversa, obtenemos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{bmatrix} 2 & 1 \\ 5 & 3 \end{bmatrix} \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix} = \begin{bmatrix} (2 \cdot 3 + 1 \cdot (-5)) & (2 \cdot (-1) + 1 \cdot 2) \\ (5 \cdot 3 + 3 \cdot (-5)) & (5 \cdot (-1) + 3 \cdot 2) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} ¡Que es la matriz identidad!

¿Cómo se calcula la inversa de matrices más grandes?

Para matrices de 3x3 o más grandes, el cálculo de la inversa es más complejo. Se usa una fórmula que involucra el determinante y algo llamado la "matriz de adjuntos" (o cofactores). Sin embargo, para matrices muy grandes, esta fórmula es muy lenta. Por eso, se usan otros métodos más eficientes.

Propiedades importantes de la Matriz Inversa

Las matrices inversas tienen algunas propiedades interesantes:

• Es única: Si una matriz tiene una inversa, solo tiene una. No puede tener dos inversas diferentes.
• Inversa de un producto: Si multiplicas dos matrices (B y C) y luego buscas la inversa de ese resultado, es lo mismo que multiplicar las inversas de C y B en orden inverso:

• Inversa de la transpuesta: La transpuesta de una matriz es cuando sus filas se convierten en columnas y sus columnas en filas. Si una matriz es invertible, su transpuesta también lo es. Además, la inversa de la transpuesta es igual a la transpuesta de la inversa:

• Doble inversa: Si calculas la inversa de una matriz y luego la inversa de esa inversa, ¡vuelves a la matriz original!

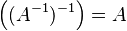
• Relación con el determinante: Una matriz solo tiene inversa si su determinante es diferente de cero.

Métodos para encontrar la Matriz Inversa

Además de las fórmulas analíticas (como la que vimos para matrices 2x2), existen otros métodos para calcular la inversa de una matriz, especialmente para las más grandes:

Método de Eliminación de Gauss-Jordan

Este es un método muy popular. Consiste en colocar la matriz original junto a una matriz identidad del mismo tamaño. Luego, se realizan una serie de operaciones matemáticas en las filas de ambas matrices al mismo tiempo, con el objetivo de transformar la matriz original en la matriz identidad. Cuando la matriz original se convierte en la identidad, la matriz que estaba al lado (la identidad original) se habrá transformado en la inversa de la matriz original.

Descomposición LU

Otro método es la descomposición LU. Este método "descompone" la matriz original en el producto de dos matrices más simples: una matriz triangular inferior (L) y una matriz triangular superior (U). Estas matrices triangulares son mucho más fáciles de invertir, lo que simplifica el proceso general.

Grupo Lineal

El conjunto de todas las matrices cuadradas que tienen inversa forma lo que se conoce como un "grupo lineal". Este concepto es muy importante en matemáticas avanzadas y en física, ya que ayuda a entender transformaciones y simetrías.

Galería de imágenes

• 

  Una forma de ver una matriz 3x3 es como 3 planos que se cruzan en un solo punto.

Véase también

En inglés: Invertible matrix Facts for Kids