Combinación lineal para niños
En matemáticas, especialmente en el álgebra lineal, una combinación lineal es una forma de juntar cosas. Imagina que tienes varios elementos, como vectores (flechas con dirección y tamaño). Una combinación lineal es cuando multiplicas cada uno de esos elementos por un número y luego sumas todos los resultados.
Por ejemplo, si tienes vectores Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_1, v_2, \dots, v_n y números Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): k_1, k_2, \dots, k_n , su combinación lineal se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v=k_1v_1+k_2v_2+\cdots+k_nv_n
Aquí, los números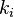 
se llaman escalares. Este concepto es muy importante para entender otras ideas en matemáticas, como la independencia lineal y las bases de un espacio vectorial.
Contenido
Combinación Lineal: ¿Qué es y para qué sirve?
La combinación lineal es una herramienta fundamental en el álgebra lineal. Nos permite expresar un elemento (como un vector) a partir de otros elementos más simples. Es como construir algo complejo usando piezas básicas.
¿Cómo se define una combinación lineal?
De manera sencilla, decimos que un elemento es una combinación lineal de otros si podemos obtenerlo multiplicando esos otros elementos por números y luego sumándolos.
Combinación lineal en espacios vectoriales
En un espacio vectorial (un conjunto de vectores donde puedes sumarlos y multiplicarlos por números), si tienes un grupo de vectores Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=\{ v_1, v_2, \dots, v_n \} , un vector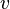 
es una combinación lineal de 
si puedes escribirlo como:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v = k_1 v_1 + k_2 v_2 + \dots + k_n v_n
donde Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): k_1, \dots, k_n son números (escalares). Esto significa que 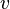se puede "formar" a partir de los vectores de .
Ejemplos de combinaciones lineales
Para entenderlo mejor, veamos algunos ejemplos:
- Imagina el punto (20, 12, 37) en un espacio tridimensional. Este punto es una combinación lineal de los puntos (1, 3, 5) y (6, 2, 9). Podemos escribirlo así:
:
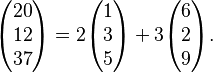Esto significa que si multiplicamos el primer vector por 2 y el segundo por 3, y luego los sumamos, obtenemos el vector (20, 12, 37).
- Si tienes un vector 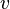, cualquier múltiplo de él, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2v o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -5v , es una combinación lineal de 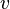. En un plano, estos múltiplos son vectores que apuntan en la misma dirección que 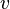(son paralelos).
- Si un vector 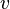en un espacio tridimensional es una combinación lineal de otros dos vectores
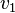y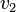 
que no son paralelos entre sí, significa que los tres vectores (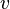, 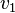y 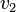) están en el mismo plano.
- En una ecuación como
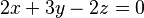, podemos decir que 
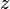es una combinación lineal de 
y 
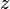. Si despejamos , obtenemos 
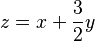. Esto muestra cómo 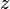se forma a partir de e .
Espacio generado: ¿Qué es y cómo se forma?
Cuando tienes un conjunto de vectores, puedes formar muchas combinaciones lineales con ellos. El espacio generado por un conjunto de vectores es el grupo de todos los vectores que puedes crear usando combinaciones lineales de esos vectores. Se escribe como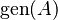 
.
En otras palabras, el espacio generado es el conjunto de todos los resultados posibles al combinar linealmente los vectores de un grupo. Este conjunto es el subespacio vectorial más pequeño que contiene a todos los vectores originales.
Galería de imágenes
-
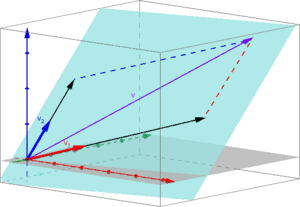
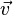es la combinación lineal de los vectores Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \vec{u}_1 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \vec{u}_2 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \vec{v} = 2 \cdot \vec{u}_1 + 1.5 \cdot \vec{u}_2
Véase también
En inglés: Linear combination Facts for Kids
