Vector, valor y espacio propios para niños

Vectores Propios: ¡Los Vectores Especiales de las Transformaciones!

En el mundo de las matemáticas, especialmente en una rama llamada álgebra lineal, existen unos vectores muy especiales conocidos como vectores propios (también llamados eigenvectores o autovectores). Imagina que tienes una flecha (un vector) y le aplicas una transformación, como girarla, estirarla o reflejarla. Los vectores propios son esas flechas que, después de la transformación, siguen apuntando en la misma dirección (o exactamente en la dirección opuesta). Lo único que cambia es su longitud, se hacen más grandes o más pequeños.

El número por el que se multiplica la longitud del vector propio se llama valor propio (o autovalor). Es como el "factor de escala" de esa transformación para ese vector en particular. A veces, una transformación se entiende mucho mejor si conocemos sus vectores y valores propios.

Un espacio propio es un grupo de vectores propios que comparten el mismo valor propio. Piensa en ello como una "familia" de vectores que se comportan de la misma manera bajo una transformación.

Fig. 1. En esta transformación de la Mona Lisa, la imagen se ha deformado de tal forma que su eje vertical no ha cambiado. El vector rojo no ha cambiado de dirección, por lo que es un vector propio de la transformación. Como no cambió de longitud, su valor propio es 1.

¿De dónde viene la palabra "Eigen"?

La palabra "eigen" viene del idioma alemán y significa "propio" o "característico". Fue usada por primera vez en este contexto por un matemático llamado David Hilbert en 1904. La idea es que estos vectores y valores son "propios" o "característicos" de una transformación específica, ayudando a entender su naturaleza única.

¿Cómo funcionan las transformaciones y los vectores?

Las transformaciones lineales son como "cambios" que se aplican a los objetos en un espacio. Por ejemplo, girar una figura, reflejarla como en un espejo o estirarla. Los vectores son como flechas que tienen una longitud y una dirección.

• Los vectores propios son esas flechas que, al aplicarles una transformación, no cambian su dirección. Solo se estiran o encogen.
• El valor propio es el número que nos dice cuánto se estira o encoge el vector propio. Si el valor propio es 2, el vector se duplica en longitud. Si es 0.5, se reduce a la mitad. Si es -1, mantiene su longitud pero apunta en la dirección opuesta.
• Un espacio propio es el conjunto de todos los vectores propios que tienen el mismo valor propio.
• La multiplicidad geométrica de un valor propio nos dice cuántas "direcciones" independientes tiene un espacio propio.
• El espectro de una transformación es el conjunto de todos sus valores propios.

Por ejemplo, si giras un objeto en el espacio, el eje de rotación es un "vector propio". Los vectores que están sobre ese eje no cambian de dirección. Su "valor propio" es 1, porque su longitud no cambia. El "espacio propio" es todo el eje de rotación.

Ejemplos de Vectores Propios en la Vida Real

• La Tierra girando: Imagina la Tierra rotando. Una flecha que va desde el centro de la Tierra hasta el Polo Norte (o Sur) no cambia de dirección mientras la Tierra gira. Esa flecha es un vector propio de la rotación de la Tierra. Su valor propio es 1, porque su longitud no cambia. Sin embargo, una flecha que va del centro al ecuador sí cambia de dirección.
• Una lámina de metal que se expande: Si una lámina de metal se expande uniformemente desde un punto central, de modo que todas las distancias desde ese punto se duplican, entonces cualquier flecha que salga del punto central es un vector propio. Su valor propio sería 2, porque todas las longitudes se duplican.
• Cuerdas vibrantes: Piensa en una cuerda de guitarra. Cuando la tocas, vibra de ciertas maneras especiales llamadas "ondas estacionarias". Estas ondas son como los "vectores propios" de la vibración de la cuerda. Mantienen su forma, pero su amplitud (su "longitud") cambia con el tiempo.

Una onda estacionaria en una cuerda fija en sus cabos. A medida que varía el tiempo, la onda estacionaria varía en amplitud, pero su forma no se modifica. Es un ejemplo de "función propia".

Casos Especiales de Transformaciones

Para entender mejor, veamos cómo se comportan los vectores propios en algunas transformaciones comunes en un plano (dos dimensiones):

• Rotación: Si giras algo, generalmente no hay vectores que mantengan su dirección original (a menos que el giro sea de 0 o 360 grados).
• Reflexión: Si reflejas algo (como en un espejo), los vectores que son paralelos al "eje del espejo" mantienen su dirección (su valor propio es 1). Los vectores que son perpendiculares al eje del espejo también mantienen su dirección, pero apuntan en sentido contrario (su valor propio es -1).
• Escalado uniforme: Si estiras o encoges todo por igual, ¡todos los vectores son vectores propios! El valor propio es el factor de escala.
• Proyección sobre una línea: Si proyectas todos los puntos sobre una línea, los vectores que ya están sobre esa línea son vectores propios (su valor propio es 1). Los vectores que son perpendiculares a esa línea se "encogen" hasta convertirse en el vector cero (su valor propio es 0).

La Ecuación de los Vectores Propios

Matemáticamente, la idea de un vector propio se expresa con una ecuación sencilla:

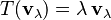
Esto significa que cuando aplicas una transformación T a un vector Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}_\lambda , el resultado es el mismo vector Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}_\lambda multiplicado por un número . Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}_\lambda es el vector propio y es su valor propio.

A menudo, las transformaciones se representan con matrices. En ese caso, la ecuación se ve así:

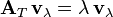
Donde Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{A}_T es la matriz que representa la transformación.

A veces, los vectores propios no son solo flechas, sino también funciones. Por ejemplo, en el caso de la cuerda vibrante, las "funciones propias" son las ondas estacionarias.

Cálculo de Valores y Vectores Propios

Para encontrar los valores y vectores propios de una matriz, los matemáticos usan algo llamado "polinomio característico". Es una ecuación especial que, al resolverla, nos da los valores propios. Una vez que tenemos los valores propios, podemos encontrar los vectores propios correspondientes.

Para matrices muy grandes, no se usa el cálculo simbólico (con ecuaciones), sino métodos numéricos que usan computadoras para encontrar aproximaciones.

Propiedades Importantes

• La multiplicidad algebraica de un valor propio nos dice cuántas veces aparece ese valor propio como solución del polinomio característico.
• Una matriz es "diagonalizable" si podemos encontrar suficientes vectores propios para formar una base completa del espacio. Esto es muy útil porque simplifica mucho el trabajo con la matriz.
• La suma de los valores propios de una matriz es igual a la suma de los elementos de su diagonal principal (llamada "traza").
• El producto de los valores propios de una matriz es igual a su "determinante", un número que nos da información sobre cómo la transformación estira o encoge el espacio.
• Si una matriz tiene un valor propio de cero, significa que la transformación "aplasta" el espacio, haciendo que algunos vectores se conviertan en el vector cero. En este caso, la matriz no tiene una transformación inversa.

Aplicaciones de los Vectores Propios

Los vectores y valores propios son herramientas muy poderosas y se usan en muchísimos campos:

• Mecánica Cuántica: En la física de lo muy pequeño, la ecuación de Schrödinger usa valores propios para representar los niveles de energía de los átomos y las moléculas. Los vectores propios son las "funciones de onda" que describen cómo se comportan las partículas.

La función de onda asociada a los estados ligados de un electrón en un átomo de hidrógeno puede verse como los vectores propios del átomo de hidrógeno. Están asociadas a los valores propios interpretados como sus energías.

• Ingeniería: Se usan para analizar la estabilidad de estructuras, el comportamiento de vibraciones en puentes o edificios, y el diseño de sistemas de control.
• Ciencia de Datos y Aprendizaje Automático: Son fundamentales en técnicas como el Análisis de Componentes Principales (PCA), que ayuda a reducir la complejidad de grandes conjuntos de datos, encontrando las "direcciones" más importantes en los datos.
• Gráficos por Computadora: Se usan para animaciones, modelado 3D y procesamiento de imágenes.
• Economía: Para analizar modelos económicos y el comportamiento de sistemas financieros.
• Biología: En modelos de poblaciones para entender cómo crecen o decrecen las especies.

Galería de imágenes

• 

  Fig. 3. Espectro de absorción de un átomo de calcio. Los picos corresponden al espectro discreto del hamiltoniano.

Véase también

En inglés: Eigenvalues and eigenvectors Facts for Kids