Vector unitario para niños
Un vector unitario o versor es como una flecha especial en matemáticas y física. Lo que lo hace especial es que su largo o tamaño (que llamamos módulo) es siempre igual a uno. Imagina que es una regla que mide exactamente 1 centímetro, 1 metro o 1 cualquier unidad que uses. Su principal función es indicar una dirección en el espacio.
Contenido
¿Cómo se escribe un vector unitario?
Para que sea fácil reconocer un vector unitario, a menudo se le pone un pequeño "sombrerito" o "techo" encima de la letra que lo representa. Por ejemplo, si un vector normal se escribe como v, su versión unitaria se escribe como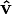 
. Esto se lee como "v gorro" o "vector v unitario".
También es común ver la notación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf u_{\text{v}} \, para indicar el vector unitario en la dirección de 
.
¿Qué es el módulo de un vector unitario?
Un vector unitario, por definición, siempre tiene un módulo igual a 1. Esto significa que su "largo" o "tamaño" es exactamente una unidad.
¿Cómo se obtiene un vector unitario?
Normalización de un vector
A veces tenemos un vector que tiene un largo diferente de 1, pero queremos encontrar un vector unitario que apunte en la misma dirección. A este proceso se le llama normalización del vector.
Para normalizar un vector, simplemente lo dividimos entre su propio módulo. Es como "encogerlo" o "estirarlo" hasta que su largo sea 1, pero sin cambiar la dirección en la que apunta.
La fórmula para hacer esto es:
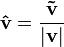
Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{\vec v} es el vector original, y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |\mathbf{v}| es su módulo (su largo). El resultado, 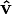, es el vector unitario que apunta en la misma dirección.
¿Para qué sirven los vectores unitarios?
Los vectores unitarios son muy útiles en física y matemáticas para simplificar cálculos y entender mejor las direcciones.
Producto escalar de vectores unitarios
Cuando multiplicamos dos vectores unitarios de una forma especial llamada producto escalar, el resultado es el coseno del ángulo que hay entre ellos. Esto es muy práctico para saber qué tan "alineados" están dos vectores.
Si tienes dos vectores unitarios, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{\hat u} y 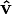, su producto escalar se calcula así:
Donde θ es el ángulo entre los dos vectores.
Proyección escalar
Los vectores unitarios también nos ayudan a encontrar la proyección escalar de un vector sobre una dirección específica. Imagina que tienes una linterna y un vector. Si apuntas la linterna en la dirección de un vector unitario, la sombra que proyecta el vector original sobre esa dirección es su proyección escalar.
Esto es muy útil en física, por ejemplo, para calcular la parte de una fuerza que actúa en una dirección particular.
Versores cartesianos: los más conocidos
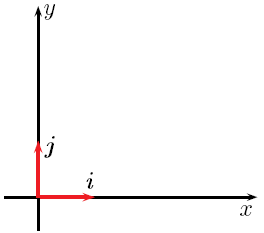
En el sistema de coordenadas cartesianas (los ejes x, y, z que usas para ubicar puntos), existen unos vectores unitarios muy famosos:
- i (o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{\hat i} ): Es el vector unitario que apunta en la dirección positiva del eje x.
- j (o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{\hat j} ): Es el vector unitario que apunta en la dirección positiva del eje y.
- k (o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{\hat k} ): Es el vector unitario que apunta en la dirección positiva del eje z.
Estos versores cartesianos nos permiten escribir cualquier vector de una manera muy sencilla usando sus componentes. Por ejemplo, un vector que va 1 unidad en x, -2 unidades en y y 3 unidades en z, se puede escribir como:
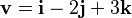
Véase también
En inglés: Unit vector Facts for Kids
- Vector
- Coordenadas cartesianas
- Módulo de un vector
