Análisis real para niños
El análisis real es una parte de las matemáticas que estudia los números reales y las funciones que trabajan con ellos. Se enfoca en entender cómo se comportan estas funciones, especialmente cuando hablamos de su límite, si son continuas (sin saltos) y cómo se relacionan con el cálculo.
El análisis real es diferente del análisis complejo, que estudia los números complejos, que son otro tipo de números.
Contenido
¿Qué estudia el análisis real?
El análisis real es una rama del análisis matemático que se dedica a entender conceptos importantes como las sucesiones (listas de números en orden), los límites (a qué valor se acerca algo), la continuidad (si una función no tiene interrupciones), la derivación (cómo cambian las funciones) y la integración (cómo calcular áreas o acumulaciones). Todo esto se hace usando los números reales.
Algunos resultados importantes en el análisis real incluyen el teorema de Bolzano-Weierstrass, el teorema de Heine-Borel, el teorema del valor medio y el teorema fundamental del cálculo. Estos teoremas son como reglas fundamentales que nos ayudan a entender mejor las funciones y los números.
Conceptos clave en el análisis real
Para empezar a estudiar el análisis real, primero se entienden los números reales. Estos números se pueden pensar como todos los puntos en una línea infinita, sin ningún hueco. Una propiedad muy importante de los números reales es la desigualdad triangular, que nos ayuda a medir distancias.
Sucesiones y series: ¿Cómo se comportan los números en orden?
Después de entender los números reales, se estudian las sucesiones. Una sucesión es una lista ordenada de números. Por ejemplo, 1, 2, 3, 4... es una sucesión. Se investiga si estas sucesiones se acercan a un valor específico, lo que se llama convergencia.
También se estudian las series, que son la suma de los términos de una sucesión. Por ejemplo, 1 + 1/2 + 1/4 + ... es una serie.
Funciones continuas: ¿Qué significa que una gráfica no tenga saltos?
Una función de variable real es como una regla que relaciona un número real con otro. Una función es continua si su gráfica se puede dibujar sin levantar el lápiz del papel. Es decir, no tiene saltos ni agujeros.
Algunos teoremas importantes sobre funciones continuas son el teorema de Bolzano, el teorema del valor intermedio y el teorema de Weierstrass. Estos teoremas nos dicen cosas interesantes sobre el comportamiento de las funciones continuas en ciertos intervalos.
Derivación: ¿Cómo medimos el cambio?
La derivada de una función nos dice qué tan rápido cambia la función en un punto específico. Es como calcular la pendiente de una curva en un punto. Con la derivada, podemos entender si una función está subiendo o bajando, y a qué velocidad.
Teoremas como el teorema de Rolle y el teorema del valor medio son fundamentales en la derivación. También se pueden construir las series de Taylor, que nos permiten aproximar funciones complicadas con polinomios más sencillos.
Integración: ¿Cómo calculamos áreas?
La integración definida nos permite calcular el "área debajo de la gráfica" de una función. Es como sumar muchas áreas pequeñas para encontrar el área total. La integración es la operación inversa de la derivación.
La integral de Riemann es una forma de calcular esta área dividiendo el espacio en pequeños rectángulos y sumando sus áreas. El teorema fundamental del cálculo es muy importante porque conecta la derivación y la integración, mostrando que son operaciones opuestas.
Los números reales: La base del análisis
Los teoremas del análisis real se basan en las propiedades de los números reales. Los números reales son un conjunto de números que incluye a los números enteros, las fracciones y los números irracionales (como pi). Se pueden representar como todos los puntos en una línea recta infinita.
Una propiedad clave de los números reales es que no tienen "huecos". Esto significa que entre dos números reales, siempre hay otro número real. Esta propiedad es fundamental para demostrar muchas cosas en el análisis real.
Propiedades de los números reales
Los números reales tienen un orden, lo que significa que podemos compararlos (saber si uno es mayor o menor que otro). Además, tienen una propiedad muy importante llamada la propiedad del límite superior mínimo. Esto significa que si tienes un conjunto de números reales que no se extienden infinitamente hacia arriba, siempre habrá un número real que es el más pequeño de todos los límites superiores posibles para ese conjunto.
Estas propiedades nos llevan a resultados importantes como el teorema de convergencia monótona y el teorema del valor intermedio.
Límites y convergencia: ¿A qué se acercan las cosas?
Un límite es el valor al que una función o una sucesión "se acerca" a medida que su entrada o su posición en la lista se aproxima a un valor específico. Esta idea es fundamental en el cálculo y el análisis matemático.
Por ejemplo, si tienes una sucesión de números como 0.9, 0.99, 0.999, 0.9999..., esta sucesión se acerca cada vez más al número 1. Decimos que el límite de esta sucesión es 1.
La idea de límite fue introducida por matemáticos como Isaac Newton y Gottfried Wilhelm Leibniz hace mucho tiempo. Más tarde, Augustin-Louis Cauchy, Bernard Bolzano y Karl Weierstrass la hicieron más precisa con una definición formal.
Definición de límite para funciones: Imagina una función f(x). Decimos que f(x) se acerca a un valor L cuando x se acerca a un número x₀ si, no importa cuán pequeño sea un número positivo que elijamos (llamado ε), siempre podemos encontrar otro número positivo (llamado δ) tal que si x está muy cerca de x₀ (a menos de δ de distancia), entonces f(x) estará muy cerca de L (a menos de ε de distancia).
Esto se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle \lim_{x\to x_0} f(x) = L}
Definición de límite para sucesiones: Para una sucesión de números (a_n), decimos que se acerca a un valor a si, para cualquier número positivo ε (por pequeño que sea), podemos encontrar un número natural N tal que todos los términos de la sucesión después de la posición N están a menos de ε de distancia de a.
Esto se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle \lim_{n \to \infty} a_n = a} Si una sucesión no se acerca a ningún valor, decimos que diverge.
Compacidad: Conjuntos "bien portados"
La compacidad es un concepto importante en matemáticas que nos ayuda a describir conjuntos de números que están "bien portados". En el caso de los números reales, un conjunto es compacto si está cerrado y acotado.
- Un conjunto cerrado significa que incluye todos sus puntos límite (los puntos a los que se pueden acercar las sucesiones dentro del conjunto).
- Un conjunto acotado significa que no se extiende infinitamente; hay un número máximo y un número mínimo que lo limitan.
Ejemplos de conjuntos compactos en los números reales incluyen un intervalo cerrado como [0, 1] (que incluye el 0 y el 1 y todos los números entre ellos). El Conjunto de Cantor es otro ejemplo interesante de un conjunto compacto.
Relación con otras áreas de las matemáticas
Las ideas del análisis real se pueden aplicar y generalizar a otros campos de las matemáticas. Por ejemplo:
- La generalización de funciones continuas y compacidad a espacios métricos y espacios topológicos conecta el análisis real con la topología general.
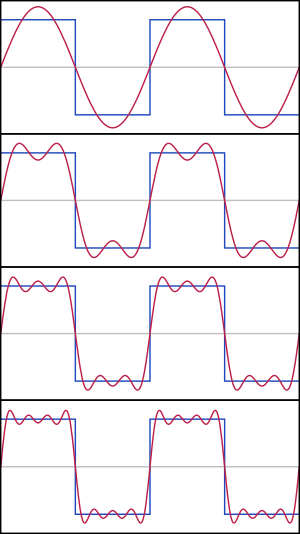
- El estudio de las sucesiones de funciones llevó al análisis de Fourier, que es útil para descomponer funciones en ondas más simples.
- La generalización de la integración a curvas y superficies en espacios de mayor dimensión dio origen al cálculo vectorial, que es importante en la geometría diferencial.
Véase también
 En inglés: Real analysis Facts for Kids
En inglés: Real analysis Facts for Kids
- Análisis complejo
- Análisis no estándar

