Espacio euclídeo para niños
El espacio euclidiano es un tipo de espacio geométrico que sigue las reglas de la geometría clásica, la que aprendemos en la escuela. Piensa en la línea recta, el plano donde dibujas o el espacio tridimensional donde vivimos; todos ellos son ejemplos de espacios euclidianos. Se les llama así por el antiguo matemático griego Euclides, quien estableció las bases de esta geometría.
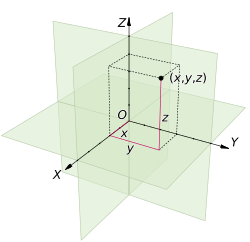
En matemáticas, el espacio euclidiano se puede describir de forma más precisa usando números. Por ejemplo, un punto en el espacio tridimensional se puede ubicar con tres números (sus coordenadas), como (x, y, z). Estos números nos ayudan a entender dónde está cada punto y cómo se relacionan entre sí.
El término "euclidiano" se usa para diferenciar estos espacios "planos" de otros espacios que son "curvos", como los que se estudian en la teoría de la relatividad de Albert Einstein. Para indicar cuántas dimensiones tiene un espacio euclidiano, se usa la letra "n", así que hablamos de un "espacio euclidiano n-dimensional", que se representa como 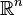 .
.
Contenido
¿Qué es el Espacio Euclidiano?
El espacio euclidiano es una forma de entender el espacio que nos rodea. Es donde las líneas son rectas, los ángulos se suman a 180 grados en un triángulo y se cumple el famoso teorema de Pitágoras. Es el modelo matemático que los antiguos griegos usaron para describir el mundo físico.
Las Dimensiones del Espacio Euclidiano
Podemos pensar en el espacio euclidiano con diferentes números de dimensiones:
- Una dimensión (1D): Es como una línea recta. Para ubicar un punto, solo necesitas un número.
- Dos dimensiones (2D): Es como un plano, una superficie plana. Para ubicar un punto, necesitas dos números (coordenadas x, y).
- Tres dimensiones (3D): Es el espacio que conocemos, donde podemos movernos hacia adelante/atrás, izquierda/derecha y arriba/abajo. Necesitas tres números (coordenadas x, y, z) para ubicar un punto.
- Más dimensiones (n-D): Aunque no podemos imaginarlos fácilmente, los matemáticos trabajan con espacios euclidianos de cuatro, cinco o más dimensiones. Esto es útil para resolver problemas complejos en ciencia e ingeniería.
Coordenadas Cartesianas y Puntos
En el espacio euclidiano, cada punto se identifica con un conjunto de números llamados coordenadas. Por ejemplo, en un plano (2D), un punto puede ser (3, 5). En el espacio (3D), podría ser (1, 2, 4). Estas coordenadas nos permiten describir la posición de cualquier objeto de manera precisa.
La Historia del Espacio Euclidiano
El concepto de espacio euclidiano tiene sus raíces en la antigua Grecia. Los geómetras de esa época, especialmente Euclides, fueron los primeros en organizar y probar las propiedades de este espacio.
Euclides y sus "Elementos"
Euclides fue un matemático griego que vivió hace más de 2000 años. Su obra más famosa, "Los Elementos", es uno de los libros más influyentes de la historia. En él, Euclides presentó la geometría de una manera muy lógica. Partió de unas pocas ideas básicas, llamadas postulados o axiomas, que se consideraban verdades evidentes. A partir de ellas, demostró todas las demás propiedades del espacio como teoremas.
Por ejemplo, uno de sus postulados dice que "por dos puntos distintos pasa exactamente una línea recta". A partir de estas ideas sencillas, Euclides construyó todo un sistema de geometría.
La Evolución de la Definición
Durante muchos siglos, la geometría de Euclides fue la única forma de entender el espacio. Sin embargo, en el siglo XVII, un matemático llamado René Descartes introdujo las coordenadas cartesianas. Esto fue un gran cambio, porque permitió usar el álgebra (cálculos con números) para resolver problemas de geometría.
Más tarde, en el siglo XIX, los matemáticos comenzaron a estudiar espacios con más de tres dimensiones y a desarrollar nuevas formas de definir el espacio euclidiano usando conceptos de álgebra, como los espacios vectoriales. Esta definición moderna es la que se usa más comúnmente hoy en día en matemáticas avanzadas.
Midiendo en el Espacio Euclidiano
Una de las cosas más importantes que podemos hacer en el espacio euclidiano es medir distancias y ángulos.
La Distancia Euclidiana
La distancia entre dos puntos en el espacio euclidiano se calcula usando una fórmula que es una generalización del teorema de Pitágoras. Si tienes dos puntos, puedes encontrar la distancia entre ellos elevando al cuadrado la diferencia de sus coordenadas, sumando esos resultados y luego sacando la raíz cuadrada. Esta es la "distancia euclidiana".
Por ejemplo, para dos puntos (x1, y1) y (x2, y2) en un plano, la distancia es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
Ángulos en el Espacio Euclidiano
También podemos definir ángulos entre líneas o vectores en el espacio euclidiano. Esto se hace usando el "producto escalar", que es una operación matemática que nos ayuda a entender cómo se relacionan las direcciones de dos objetos.
Más Allá del Espacio Euclidiano
Aunque el espacio euclidiano es muy útil y describe bien nuestro mundo a escala humana, los matemáticos y físicos han descubierto otros tipos de espacios.
Espacios Curvos
Existen las "geometrías no euclidianas", donde las reglas son diferentes. Por ejemplo, en una superficie curva como la de una esfera, la suma de los ángulos de un triángulo no es 180 grados. Estos espacios curvos son importantes para entender fenómenos como la gravedad en la teoría de la relatividad.
Espacios de Dimensión Infinita
Aunque es difícil de imaginar, los matemáticos también estudian espacios euclidianos con un número infinito de dimensiones. Estos espacios son muy abstractos, pero son herramientas poderosas en áreas como el análisis matemático y la física teórica.
Galería de imágenes
Véase también
 En inglés: Euclidean space Facts for Kids
En inglés: Euclidean space Facts for Kids