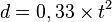Función (matemática) para niños

Enciclopedia para niños

En matemáticas, una función es como una máquina especial que toma un valor de "entrada" y lo transforma en un único valor de "salida". Piensa en ella como una regla que conecta elementos de un grupo con elementos de otro grupo.

Por ejemplo, el área de un círculo depende de su radio. Si conoces el radio, puedes calcular el área. Aquí, el área es la "salida" y el radio es la "entrada". A la entrada se le llama variable independiente y a la salida se le llama variable dependiente.

Otro ejemplo: cada número entero tiene un único número cuadrado.

...	−2 → +4,	−1 → +1,	0 → 0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

Esta es una función que toma un número entero y te da su cuadrado.

También puede haber funciones que no usan números. Por ejemplo, una función que a cada palabra en español le asigna su primera letra:

...,

Estación → E,

Museo → M,

Arroyo → A,

Rosa → R,

Avión → A,

...

Esta función toma una palabra y te da su letra inicial.

Una función se suele escribir así:

f: A → B

a → f(a),

Aquí, f es el nombre de la función. A es el conjunto de todas las posibles "entradas" (se llama dominio), y B es el conjunto de todas las posibles "salidas" (se llama codominio). f(a) es el resultado que obtienes cuando pones a en la función.

¿Qué es una Función?

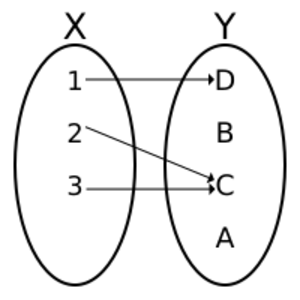
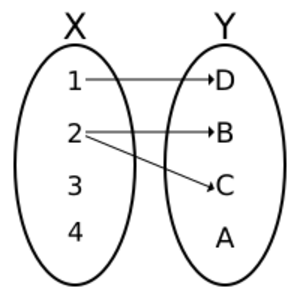
Una función es una regla que asigna a cada elemento de un primer conjunto (el dominio) un único elemento de un segundo conjunto (el codominio). Es como una relación especial donde cada entrada tiene solo una salida.

Variables en las Funciones

Cuando hablamos de funciones, usamos el término variable independiente para la entrada (el valor que tú eliges o que cambia libremente). La variable dependiente es la salida, cuyo valor "depende" de la variable independiente.

Ejemplos Cotidianos de Funciones

Imagina un coche que se mueve. La distancia que recorre el coche depende del tiempo que ha estado en movimiento.

La distancia es la variable dependiente.
El tiempo es la variable independiente.

Si el coche acelera a 0.66 metros por segundo al cuadrado, la distancia d que recorre en un tiempo t se puede calcular con la fórmula:

d=0,33 \times t^2

Cómo se Escribe una Función

Las funciones se pueden escribir de varias maneras:

Con una fórmula o ecuación: Como 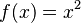$f(x) = x^2$ para la función "cuadrado".
Con una tabla de valores: Donde se muestran algunas entradas y sus salidas correspondientes.

Tiempo t (s)	Distancia d (m)
0,0	0,0
0,5	0,1
1,0	0,3
1,5	0,7
2,0	1,3
2,5	2,0

Con pares ordenados: Como {(-2, 0), (-1, 1), (0, 2), (1, 3), ...} para la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = x+2 .

Formas de Representar Funciones

Las funciones se pueden visualizar de diferentes maneras:

Expresión matemática: Una fórmula como $y=f(x)$ .
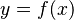Tabulación: Una tabla con valores de entrada y salida.
Pares ordenados: Listas de (entrada, salida).
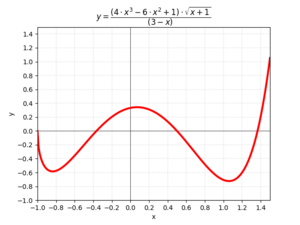
Gráfica: Un dibujo en un plano de coordenadas que muestra cómo se relacionan las entradas y salidas. Esto es muy útil para ver el comportamiento de la función.

La curva roja es la gráfica de una función, porque cualquier línea vertical tiene exactamente un punto de cruce con la curva.

Un Poco de Historia de las Funciones

El concepto de función, tal como lo conocemos hoy, no apareció hasta el siglo XVII. Matemáticos como René Descartes, Isaac Newton y Gottfried Leibniz empezaron a pensar en las funciones como una relación entre dos cantidades que cambian. Leibniz fue quien usó por primera vez palabras como "función", "variable" y "constante". La forma de escribir f(x) fue usada por primera vez por Alexis Claude Clairaut y Leonhard Euler en el siglo XVIII.

Al principio, una función se veía como una fórmula. Pero en 1837, el matemático alemán Peter Gustav Lejeune Dirichlet propuso la definición moderna: una función es cualquier correspondencia entre dos conjuntos de números, donde cada número del primer conjunto se asocia con un único número del segundo. Con el tiempo, la idea de función se hizo más abstracta y se aplicó a cualquier tipo de objetos, no solo números.

Partes Clave de una Función

Dominio y Codominio: Los Conjuntos de una Función

El dominio (o conjunto de partida) es el grupo de todas las entradas posibles que la función puede aceptar.
El codominio (o conjunto de llegada) es el grupo de todas las posibles salidas que la función podría producir.

Diagrama de una función.

Diagrama de una relación que no es una función. Una razón es que 2 es el primer elemento en más de un par ordenado. Otra razón es que ni 3 ni 4 son primeros elementos (entrada) de ningún par ordenado.

Imagen y Preimagen: Los Resultados de una Función

La imagen de un elemento es el resultado específico que la función produce para esa entrada. Por ejemplo, si 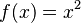$f(x) = x^2$ , la imagen de 3 es 9.
El rango o recorrido de la función es el conjunto de todas las imágenes posibles que la función realmente produce. Es un subconjunto del codominio.
La preimagen (o imagen inversa) de un elemento del codominio es el conjunto de todas las entradas del dominio que producen esa salida específica. Por ejemplo, la preimagen de 4 para 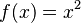$f(x) = x^2$ sería {-2, 2}.

La anti-imagen de cada partido es el conjunto de los electores que lo votaron.

¿Cuándo son Iguales Dos Funciones?

Dos funciones son iguales si cumplen tres cosas:

Tienen el mismo dominio (las mismas entradas posibles).
Tienen el mismo codominio (las mismas salidas posibles).
Para cada entrada, producen exactamente la misma salida.

Tipos Especiales de Funciones

Las funciones se pueden clasificar según cómo se relacionan sus entradas y salidas.

Funciones Inyectivas: Sin Repeticiones

Una función es inyectiva si cada salida diferente proviene de una entrada diferente. Es decir, si dos entradas son distintas, sus salidas también lo serán. No hay dos entradas que den la misma salida.

Funciones Sobreyectivas: Cubriendo Todo

Una función es sobreyectiva si su rango (todas las salidas que produce) es igual a su codominio (todas las salidas posibles). Esto significa que cada elemento del codominio es la imagen de al menos una entrada del dominio.

Funciones Biyectivas: El Emparejamiento Perfecto

Una función es biyectiva si es inyectiva y sobreyectiva al mismo tiempo. Esto significa que cada entrada tiene una única salida, y cada salida tiene una única entrada que la produce. Es como un emparejamiento uno a uno perfecto.

Operaciones con Funciones

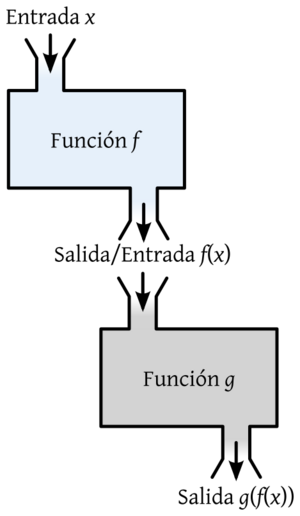
Composición de Funciones: Una Función Dentro de Otra

La composición g ∘ f actúa sobre el objeto x transformándolo según f, y después transformando f(x) mediante g.

La composición de funciones es cuando aplicas una función y luego aplicas otra función al resultado de la primera. Si tienes una función f y luego una función g, la composición se escribe g ∘ f. Esto significa que primero aplicas f y luego g al resultado de f.

Por ejemplo, si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h_1(x) = x^2 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h_2(x) = x+1 :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (h_1 \circ h_2)(x) significa Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h_1(x+1) = (x+1)^2 .
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (h_2 \circ h_1)(x) significa Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h_2(x^2) = x^2+1 .

Como ves, el orden importa.

La Función Identidad: El "No Hago Nada"

La función identidad es una función que toma una entrada y devuelve exactamente la misma entrada. Es como si no hiciera nada. Si tienes un conjunto A, la función identidad de A se escribe id_A y hace que id_A(a) = a.

La Función Inversa: Deshaciendo el Camino

Una función inversa es como la función que "deshace" lo que hizo la función original. Si una función f toma a y lo convierte en b, su inversa f⁻¹ toma b y lo convierte de nuevo en a. No todas las funciones tienen inversa; solo las funciones biyectivas la tienen.

Por ejemplo, si la función "cubo" es 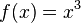$f(x) = x^3$ , su inversa es la función "raíz cúbica", Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f^{-1}(x) = \sqrt[3]{x} .

Restricción y Extensión de Funciones

La función que asigna a cada mujer del electorado su voto es una restricción de la función que a cada miembro del electorado le asigna su voto.

La restricción de una función es cuando tomas una función y la aplicas solo a una parte de su dominio original. Es como si tuvieras una regla para todo un grupo, pero decides aplicarla solo a un subgrupo. La función original se llama entonces una extensión de la función restringida.

Funciones con Varias Entradas

Algunas funciones necesitan más de una entrada para dar una salida. A estas se les llama funciones multivariables o funciones de varias variables.

Por ejemplo, el tiempo de viaje en coche depende de la distancia y de la velocidad. Aquí, la distancia y la velocidad son las dos variables independientes. La función toma una pareja de valores (distancia, velocidad) y te da un único valor (tiempo).

Galería de imágenes

En la imagen de una relación entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados.
Una función vista como una «caja negra», que transforma los valores u objetos de «entrada» en los valores u objetos de «salida».
Representación gráfica de la posición de un cuerpo acelerado a 0,66 m/s².
Gottfried Leibniz acuñó el término «función» en el siglo XVII.

Véase también

En inglés: Function (mathematics) Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Función_(matemática)&oldid=4762105»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Función (matemática) para Niños. Enciclopedia Kiddle.