Serie (matemática) para niños
En matemática, una serie es como una suma muy larga, ¡tan larga que nunca termina! Imagina que tienes una lista de números, uno tras otro, que nunca se acaba. Una serie es el resultado de sumar todos esos números.
Se escribe con un símbolo especial llamado sumatorio, que parece una letra "E" grande:
Aquí, cada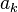 
es un número de la lista, y los puntos suspensivos (
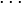) significan que la suma sigue y sigue para siempre.
Para entender una serie, no podemos sumar todos los números de golpe porque son infinitos. En cambio, usamos un truco: sumamos los primeros números, luego los primeros dos, luego los primeros tres, y así sucesivamente. A estas sumas las llamamos sumas parciales.
Por ejemplo, si nuestra lista de números es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{a_1, a_2, a_3, \ldots\} :
- La primera suma parcial es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_1 = a_1 .
- La segunda suma parcial es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_2 = a_1 + a_2 .
- La tercera suma parcial es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_3 = a_1 + a_2 + a_3 .
- Y así, la suma parcial número
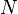es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_N = a_1 + a_2 + \cdots + a_N .
Lo que hacemos es ver qué pasa con estas sumas parciales a medida que sumamos más y más números.
Contenido
¿Qué es una Serie Matemática?
Una serie matemática es una forma de sumar una lista infinita de números. Cada número en la lista se llama "término". Por ejemplo, si tienes la lista de números 1, 2, 3, 4, y así hasta el infinito, la serie sería 1 + 2 + 3 + 4 + ...
¿Cómo se calcula una serie?
Como no podemos sumar infinitos números uno por uno, los matemáticos usan una idea llamada "límite". Imagina que las sumas parciales (S1, S2, S3...) se acercan cada vez más a un número específico. Si se acercan a un número, decimos que la serie es convergente y ese número es su "suma total". Si las sumas parciales no se acercan a un número (por ejemplo, crecen sin parar o saltan de un lado a otro), decimos que la serie es divergente.
La suma de una serie convergente se escribe así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S = \lim_{N \to \infty} S_N = \lim_{N \to \infty} \sum_{n=1}^{N} a_n = \sum_{n=1}^\infty a_n = a_1+a_2+a_3+\cdots +a_N+ \cdots
Esto significa que la suma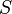 
es el límite al que se acercan las sumas parciales 
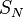cuando 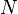(el número de términos que sumamos) se hace infinitamente grande.
La paradoja de Aquiles y la tortuga
Hace mucho tiempo, el filósofo Zenón de Elea propuso una paradoja para mostrar lo extraño que puede ser el infinito. En su historia, Aquiles (un corredor muy rápido) persigue a una tortuga. Zenón decía que Aquiles nunca alcanzaría a la tortuga.
¿Por qué? Porque para que Aquiles alcance a la tortuga, primero debe llegar al punto donde la tortuga estaba al principio. Pero cuando Aquiles llega a ese punto, la tortuga ya se ha movido un poco más. Luego, Aquiles debe llegar a ese nuevo punto, pero la tortuga ya se habrá movido otra vez, y así sucesivamente. Parece que siempre habrá una pequeña distancia que Aquiles debe cubrir.
Zenón dividió la carrera en infinitas partes. Cada parte toma un poco de tiempo. La suma de todos esos pequeños tiempos es una serie infinita. La solución a la paradoja es que, aunque hay infinitas partes, la suma total de los tiempos es un número finito. ¡Así que Aquiles sí alcanza a la tortuga! Esta paradoja ayudó a los matemáticos a entender mejor cómo las sumas infinitas pueden tener un resultado finito.
Tipos de Series
Existen muchos tipos de series, y cada una tiene características especiales.
Serie Geométrica
Una serie geométrica es una serie donde cada término se obtiene multiplicando el anterior por un número fijo, llamado "razón" (
). Por ejemplo, si la razón es 
:
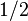Esta serie es convergente y su suma es 2. Piensa en un pastel: si te comes la mitad, luego la mitad de lo que queda, luego la mitad de lo que queda, y así sucesivamente, ¡al final te habrás comido todo el pastel!
Una serie geométrica es convergente si el valor absoluto de la razón (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |r| ) es menor que 1. Si es así, la suma es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S = \frac{1}{1 - r} .
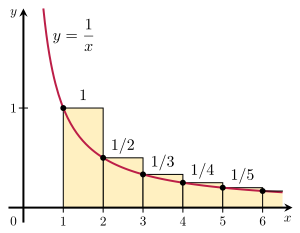
Serie Armónica
La serie armónica es:
Aunque los términos se hacen cada vez más pequeños, esta serie es divergente. Esto significa que si sigues sumando, el resultado crecerá sin límite, ¡hasta el infinito!
Series Alternadas
Una serie alternada es una serie donde los signos de los términos van cambiando, de positivo a negativo y viceversa:
Esta serie es un ejemplo de serie convergente.
Representación Decimal
Los números decimales que conoces también pueden verse como series. Por ejemplo, el número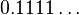 
(que es lo mismo que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1/9 ) se puede escribir como una serie:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{n=1}^\infty \frac{1}{10^n} = \frac{1}{10} + \frac{1}{100} + \frac{1}{1000} + \cdots
Estas series siempre convergen a un número real.
¿Cómo saber si una serie converge o diverge?
Los matemáticos han desarrollado "criterios de convergencia" para saber si una serie es convergente o divergente sin tener que calcular su suma exacta.
Criterio del término general
Una regla importante es que si una serie es convergente, entonces sus términos individuales (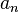
) deben acercarse a cero a medida que 
se hace muy grande. Si los términos no se acercan a cero, ¡la serie definitivamente es divergente! Sin embargo, si los términos sí se acercan a cero, no significa automáticamente que la serie sea convergente (como vimos con la serie armónica).
Otros criterios
Existen otros métodos para determinar la convergencia, como el criterio del cociente o el Criterio de la raíz, que analizan qué tan rápido disminuyen los términos de la serie. También se pueden comparar series desconocidas con series que ya sabemos si convergen o divergen.
).Operaciones con Series
Podemos sumar series o multiplicarlas por un número.
- Suma de series: Si tienes dos series convergentes, puedes sumarlas término a término para obtener una nueva serie que también converge.
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{n=1}^\infty a_n + \sum_{n=1}^\infty b_n = \sum_{n=1}^\infty (a_n + b_n)
- Multiplicación por un número: Si multiplicas todos los términos de una serie convergente por un número, la nueva serie también será convergente.
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c \sum_{n=1}^\infty a_n = \sum_{n=1}^\infty (c \cdot a_n)
Véase también
En inglés: Series Facts for Kids
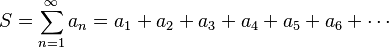
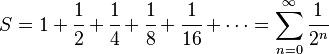
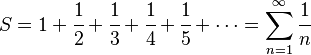
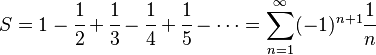
