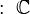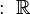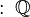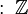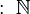Número para niños
Un número es una idea matemática que usamos para contar cosas, medir tamaños y poner etiquetas. Los números más fáciles de entender y que usamos todos los días son los números naturales: 1, 2, 3, y así sucesivamente. Se representan con el símbolo 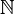 y también nos ayudan a ordenar cosas (primero, segundo, etc.). A veces, cuando decimos "número", en realidad nos referimos a un símbolo o cifra, como los números arábigos que usamos. En matemáticas, un número puede ser cualquier elemento dentro de un sistema numérico.
y también nos ayudan a ordenar cosas (primero, segundo, etc.). A veces, cuando decimos "número", en realidad nos referimos a un símbolo o cifra, como los números arábigos que usamos. En matemáticas, un número puede ser cualquier elemento dentro de un sistema numérico.
Los números son muy importantes en las ciencias. No solo los naturales, sino muchos otros tipos de números que estudian las matemáticas. El conjunto de números enteros (representados por 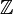 ) incluye los números naturales y también los negativos. Los números negativos nos sirven para representar, por ejemplo, deudas o temperaturas bajo cero. Si añadimos los números que son fracciones (como 1/3, 0.75 o -3.25), obtenemos los números racionales, cuyo símbolo es
) incluye los números naturales y también los negativos. Los números negativos nos sirven para representar, por ejemplo, deudas o temperaturas bajo cero. Si añadimos los números que son fracciones (como 1/3, 0.75 o -3.25), obtenemos los números racionales, cuyo símbolo es 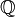 .
.
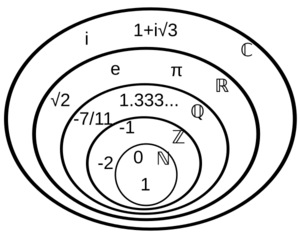
Hace mucho tiempo, se descubrió que hay números que no son racionales. Por ejemplo, la diagonal de un cuadrado con lado 1 mide raíz de 2, un número que no se puede escribir como un número entero ni como una fracción. A estos se les llama números irracionales. Los números racionales junto con los irracionales forman el conjunto de los números reales, que se representan con 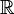 . Más tarde, se han añadido otros tipos de números, como los imaginarios y los complejos.
. Más tarde, se han añadido otros tipos de números, como los imaginarios y los complejos.
La teoría de números es una parte de las matemáticas que estudia principalmente los números enteros. Los primeros números que el ser humano inventó fueron los naturales, que se usaban para contar elementos de un grupo.
Contenido
- Tipos de números: ¿Cuáles existen?
- Estructura de los sistemas numéricos
- Números naturales especiales
- Historia del concepto de número
- Las fracciones unitarias egipcias
- Fracciones sexagesimales babilónicas
- Descubrimiento de los números inconmensurables
- Creación del cero
- Números negativos
- Transmisión del sistema indo-arábigo a Occidente
- Las fracciones continuas
- Primera formulación de los números complejos
- Generalización de las fracciones decimales
- El principio de inducción matemática
- Descubrimiento de los números trascendentes
- Teorías de los irracionales
- Álgebras hipercomplejas
- Teoría de conjuntos
- Importancia social de los números
- Sistemas de representación de los números
- Véase también
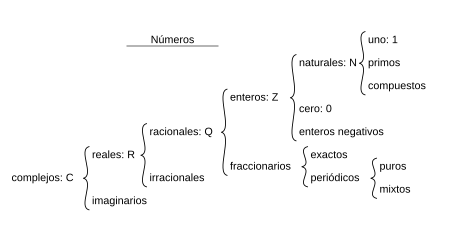
Tipos de números: ¿Cuáles existen?
Los números naturales son los más conocidos. Se representan con 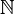 y son los más sencillos, usados para contar unidades. Si a estos les añadimos los números negativos, formamos el conjunto de los números enteros, que se representan con
y son los más sencillos, usados para contar unidades. Si a estos les añadimos los números negativos, formamos el conjunto de los números enteros, que se representan con 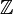 . Los números enteros negativos nos permiten, por ejemplo, representar deudas o calcular restas como 3 - 5 = -2.
. Los números enteros negativos nos permiten, por ejemplo, representar deudas o calcular restas como 3 - 5 = -2.
Otro tipo de números muy usados son los fraccionarios, que representan partes de una unidad o números mixtos. Los números fraccionarios siempre se pueden escribir como la división de dos números enteros. El conjunto de todos los números fraccionarios se llama números racionales y se representa con 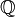 . Con los racionales, podemos hacer divisiones que no dan un resultado entero, como 15 dividido por 2, que es 7.5.
. Con los racionales, podemos hacer divisiones que no dan un resultado entero, como 15 dividido por 2, que es 7.5.
Los números racionales nos ayudan a resolver muchos problemas, pero desde la antigua Grecia se sabe que algunas medidas geométricas, como la diagonal de un cuadrado de lado 1, no son números enteros ni racionales. Estos son los números irracionales. Los números racionales y los irracionales juntos forman el conjunto de los números reales, que se representa con 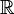 . Dentro de los números reales, hay algunos que no son soluciones de ecuaciones sencillas, y a esos se les llama números trascendentes. Los más famosos son el número π (Pi) y el número e.
. Dentro de los números reales, hay algunos que no son soluciones de ecuaciones sencillas, y a esos se les llama números trascendentes. Los más famosos son el número π (Pi) y el número e.
Un problema con los números reales es que no todas las ecuaciones tienen solución dentro de ellos. Por eso se crearon los números complejos, representados con 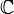 . Estos números son muy útiles en la física y en otras áreas de las matemáticas. Todos estos conjuntos de números (
. Estos números son muy útiles en la física y en otras áreas de las matemáticas. Todos estos conjuntos de números (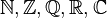 ) se han "descubierto" o sugerido al intentar resolver problemas de la vida real o de las matemáticas.
) se han "descubierto" o sugerido al intentar resolver problemas de la vida real o de las matemáticas.
Además de los números reales y complejos, existen otros tipos de números más abstractos, creados por matemáticos para generalizar el concepto de número. La mayoría de estas generalizaciones se usan solo en matemáticas, aunque algunas han encontrado aplicaciones en la física. Entre ellos están los números hipercomplejos, como los cuaterniones, que son útiles para representar giros en el espacio.
También se han creado conjuntos de números para trabajar con cantidades infinitas o muy pequeñas, como los hiperreales y los transfinitos.
Lista de los tipos de números más comunes
La teoría de los números estudia las propiedades de los números naturales y enteros. El álgebra y el cálculo nos ayudan a definir la mayoría de los sistemas numéricos, entre los que se encuentran:
- Números naturales
- Números enteros
- Números racionales
- Números reales
- Extensiones de los números reales
- Números complejos
- Números hipercomplejos
- Cuaterniones
- Octoniones
- Números hiperreales
- Números superreales
- Números surreales
- Números usados en teoría de conjuntos
- Números ordinales
- Números cardinales
- Números transfinitos
Estructura de los sistemas numéricos
En matemáticas avanzadas, un sistema numérico se define por cómo se relacionan sus elementos. Esto incluye:
- Estructura algebraica: Cómo se combinan los números con operaciones como la suma y la multiplicación.
- Estructura de orden: Cómo se comparan los números entre sí (cuál es mayor o menor). Los números naturales, enteros, racionales y reales tienen un orden claro, pero los complejos no.
- Estructura topológica: Cómo se agrupan los números y qué tan "cerca" están unos de otros.
Muchos conjuntos de números se pueden representar con diagramas de Hasse, diagramas de Euler y diagramas de Venn. Históricamente, los diferentes conjuntos numéricos se han construido desde los más simples hasta los más complejos.
Números naturales especiales
El estudio de las propiedades de los números ha llevado a descubrir muchos tipos de números interesantes, algunos de ellos más por diversión matemática que por su utilidad práctica. Aquí te mostramos algunos:
- Perfecto: Un número que es igual a la suma de sus divisores (incluyendo el 1). Por ejemplo: 6 = 1 + 2 + 3.
- Sheldon: El número 73. Es el 21º número primo, y si multiplicas sus dígitos (7 × 3) obtienes 21. Además, si inviertes sus dígitos, obtienes 37, que es el 12º número primo.
- Narcisista: Un número de "n" dígitos que es igual a la suma de cada uno de sus dígitos elevado a la potencia "n". Ejemplo: 153 = 1³ + 5³ + 3³.
- Omirp: Un número primo que, al invertir sus dígitos, da otro número primo. Ejemplo: 1597 y 7951 son primos.
- Vampiro: Un número que es el resultado de multiplicar dos números que se forman con sus propios dígitos. Ejemplo: 2187 = 27 × 81.
- Pitagórico: Una terna pitagórica son tres números enteros que cumplen que el cuadrado de uno más el cuadrado de otro es igual al cuadrado del tercero. Por ejemplo: (3, 4, 5) porque 3² + 4² = 9 + 16 = 25 = 5².
Una vez que se entendió qué son los números, surgió el desafío de cómo escribirlos. El sistema que usamos hoy, la numeración posicional, se hizo popular gracias a la invención del cero.
El matemático Gottlob Frege (1848-1925) dio una definición de "número" que fue muy importante. Dijo que "n" es un número si existe un concepto para el cual "n" se aplica, es decir, si se puede establecer una relación "uno a uno" entre los elementos.
El matemático Giuseppe Peano (1858-1932) estableció cinco reglas básicas para los números naturales:
- 0 es un número natural.
- Todo número natural tiene un sucesor (el siguiente número).
- Dos números diferentes no tienen el mismo sucesor.
- 0 no es el sucesor de ningún número.
- Y la propiedad inductiva (si una propiedad es cierta para 0 y para el sucesor de cualquier número que la cumpla, entonces es cierta para todos los números naturales).
Historia del concepto de número
La idea de número está relacionada con nuestra capacidad de contar y comparar qué grupo de cosas tiene más elementos. Las primeras sociedades humanas necesitaban saber cuántos elementos había en una colección. Esto se resolvía simplemente contando. Aunque la mayoría de las culturas tienen sistemas para contar hasta cientos, algunos pueblos antiguos solo tenían palabras para 1, 2 y 3, y usaban "muchos" para cantidades mayores.
El conteo comenzó usando objetos físicos, como montones de piedras, o marcas en huesos. Se han encontrado huesos tallados con muescas de hace unos 37,000 años, que podrían estar relacionados con el registro de las fases de la luna. Los sistemas de conteo de muchas lenguas muestran que contar se hacía con los dedos, por eso los sistemas de base 10 (decimal) y base 20 (vigesimal) son los más comunes.
El paso a usar símbolos para los números, al igual que la escritura, se relaciona con el surgimiento de sociedades más complejas que necesitaban llevar registros de impuestos y propiedades. Los símbolos numéricos más antiguos se encontraron en las civilizaciones de Mesopotamia, donde se usaban para contabilidad, comercio, agrimensura y astronomía.
En general, desde hace unos 5,000 años, la mayoría de las civilizaciones han contado de forma similar a como lo hacemos hoy, aunque la manera de escribir los números ha sido muy variada. Se pueden clasificar en tres tipos:
- Sistemas de notación aditiva. Se sumaban los símbolos de unidades, decenas, centenas, etc. para formar el número. Por ejemplo, los sistemas egipcio y romano.
- Sistemas de notación híbrida. Combinaban la suma con la multiplicación. Por ejemplo, para 500, en lugar de cinco símbolos de 100, usaban una combinación del 5 y el 100. El orden de los símbolos era importante. Ejemplos son el sistema chino clásico y el maya. El sistema maya fue el primero en usar el cero como lo conocemos hoy (alrededor del año 36 a. C.).
- Sistemas de notación posicional. La posición de cada cifra indica su valor (unidades, decenas, centenas, etc.). Solo tres culturas, además de la india, desarrollaron este sistema: el sistema chino (300 a. C.) que no tenía cero, el sistema babilónico (2000 a. C.) que usaba base 60 y no tenía cero hasta el 300 a. C., y el sistema indio, que es la base de nuestros números actuales.
Las fracciones unitarias egipcias
En el Papiro de Ahmes/Rhind, que data de 2000 a 1800 a. C., se muestra cómo los egipcios trabajaban con fracciones. Ellos usaban principalmente fracciones unitarias (como 1/2, 1/3, 1/4), representadas con un signo ovalado sobre el número. La fracción 2/3 tenía un signo especial. Para calcular, usaban "duplicaciones" y "mediaciones" en lugar de nuestra multiplicación y división.
Fracciones sexagesimales babilónicas
En las tablillas de arcilla de la dinastía Hammurabi (1800-1600 a. C.), los babilonios usaban un sistema posicional que también incluía fracciones. Su sistema era de base 60. Para hacer cálculos, usaban muchas tablas (de multiplicar, de inversos, de raíces, etc.).
Descubrimiento de los números inconmensurables
No se sabe con exactitud cuándo ni cómo se descubrieron, pero se atribuye a la escuela pitagórica. Aristóteles (384-322 a. C.) mencionó una prueba de que la diagonal de un cuadrado no se puede medir exactamente con su lado usando números racionales. Esto causó un gran problema para la idea pitagórica de que "todo es número".
El matemático Eudoxo de Cnido (408-355 a. C.) resolvió este problema con una definición que se parece mucho a la de los números reales que se usaría mucho después.
Creación del cero
En los sistemas de numeración posicional, a veces faltaba un valor para indicar la ausencia de unidades en una posición. Por ejemplo, en el sistema babilónico, el número 32 podía significar 3x60 + 2 o 3x60² + 0x60 + 2. A veces dejaban un espacio vacío, pero era fácil confundirse.
En Grecia, alrededor del siglo III a. C., se usaba una "o" para representar la nada, pero no era el concepto de cero que tenemos hoy. La idea del cero como un concepto matemático parece haber surgido en la India.
En América, la primera vez que se usó el cero fue en una estela olmeca tardía del siglo III a. C. Los mayas también inventaron varios símbolos para el cero.
Números negativos
Brahmagupta, en el año 628 d. C., fue el primero en sistematizar la aritmética de los números positivos, negativos y el cero. Él los llamaba "los bienes" (positivos), "las deudas" (negativos) y "la nada" (cero). Por ejemplo, estableció reglas para la división, como "positivo dividido por positivo es afirmativo" o "positivo dividido por negativo es negativo". Él usó los negativos en los cálculos sin necesidad de relacionarlos con la geometría.
Los chinos también tenían la idea de números negativos y los usaban en sus cálculos con varillas de diferentes colores.
Transmisión del sistema indo-arábigo a Occidente
Varios autores del siglo XIII ayudaron a difundir el sistema numérico que usamos hoy. Destaca Fibonacci (1180-1250), quien viajó por Oriente y aprendió de los árabes el sistema posicional hindú. Escribió un libro llamado El Liber abaci, donde explicaba la numeración posicional y las operaciones básicas. Sin embargo, no incluyó los números negativos, ya que los árabes tampoco los consideraban importantes en ese momento.
Las fracciones continuas
Pietro Antonio Cataldi (1548-1626) desarrolló una forma de calcular raíces cuadradas usando fracciones continuas, similar a como lo hacemos hoy. Esto ayudó a que los números irracionales fueran aceptados, ya que se podían aproximar fácilmente con números racionales.
Primera formulación de los números complejos
Los números complejos al principio no eran muy aceptados. Se les llamaba "ficticios" o "imaginarios" porque no se creía que tuvieran una existencia real. Sin embargo, matemáticos como Gerolamo Cardano (1501-1576) y Rafael Bombelli (1526-1573) los usaron para resolver ecuaciones, aunque los consideraban solo herramientas matemáticas. Bombelli fue quien estableció las reglas para operar con ellos.
Generalización de las fracciones decimales
Aunque las fracciones decimales se usaban ocasionalmente en la Edad Media, su uso se hizo popular con la obra de Simon Stevin en 1585, De Thiende (La Disme). Él propuso un sistema para escribir números decimales sin usar fracciones. Esta notación fue simplificada más tarde por otros matemáticos, usando un punto o una coma para separar la parte entera de la decimal.
El principio de inducción matemática
Este es un método de demostración matemática. Blaise Pascal (1623-1662) lo usó para probar propiedades del triángulo numérico que lleva su nombre. La inducción matemática tiene dos partes:
- Paso base: Demostrar que una propiedad es cierta para el primer número (por ejemplo, 0 o 1).
- Paso inductivo: Demostrar que si la propiedad es cierta para un número cualquiera, entonces también es cierta para el siguiente número.
Si se cumplen estas dos partes, la propiedad es cierta para todos los números. Imagina una fila de fichas de dominó: el paso base es empujar la primera ficha, y el paso inductivo es que si una ficha cae, la siguiente también caerá. Así, todas las fichas caerán.
Descubrimiento de los números trascendentes
La diferencia entre números irracionales algebraicos y trascendentes se empezó a entender en el siglo XVIII. Matemáticos como Leonhard Euler y Lambert demostraron que números como e y π son irracionales. Más tarde, Liouville, Hermite y Lindeman probaron la existencia de los números trascendentes, que son aquellos que no pueden ser la solución de una ecuación algebraica con coeficientes racionales.
Teorías de los irracionales
Hasta mediados del siglo XIX, los matemáticos tenían una idea intuitiva de los números. Luego, se buscó una base lógica más sólida para los números reales. Varios matemáticos, como Richard Dedekind y Georg Cantor, desarrollaron teorías para definir los números reales de manera más precisa, basándose en la continuidad de la recta numérica o en sucesiones de números racionales.
Álgebras hipercomplejas
La forma en que se construyeron los números complejos a partir de los reales llevó a los matemáticos a crear otras generalizaciones llamadas números hipercomplejos. Estos sistemas numéricos incluyen a los números complejos, pero su multiplicación no siempre es conmutativa (el orden de los factores altera el producto).
Teoría de conjuntos
La teoría de conjuntos dio nuevas formas de extender los números naturales y reales. La idea de conjuntos con un número infinito de elementos llevó a la aritmética de números transfinitos, introducidos por Georg Cantor en 1873.
Los números hiperreales son otra extensión de los números reales, usados en un área llamada análisis no estándar. Aunque no siempre dan resultados nuevos, a veces simplifican las demostraciones matemáticas.
Importancia social de los números
- Los números naturales surgieron por la necesidad de contar.
- Los números fraccionarios, por la necesidad de medir partes de un todo y compartir.
- Los enteros negativos, para representar situaciones con doble sentido, como ganancias y pérdidas.
- Los números reales, para medir segmentos y distancias.
- Los números complejos, para resolver ecuaciones algebraicas que no tenían solución con los números reales.
Sistemas de representación de los números
Cifra, dígito y numeral
Una forma común de escribir números es usando un conjunto limitado de símbolos, llamados dígitos. Al combinarlos, formamos cifras que representan números. Cuando una secuencia específica de signos se usa para representar un número, se le llama numeral.
Base numérica
Tanto los idiomas como la mayoría de los sistemas de escritura de números usan un número limitado de símbolos para expresar una cantidad mucho mayor de números. Una forma importante de lograr esto es usando una base aritmética. En estos sistemas, un número se expresa sumando o multiplicando valores. En los sistemas posicionales, cada símbolo tiene un valor diferente según su posición. Por ejemplo, en el número 13568 (base 10):
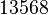
El 8 está en la posición de las unidades, el 6 en las decenas, el 5 en las centenas, el 3 en los millares y el 1 en las decenas de millares. Esto significa que el número es:
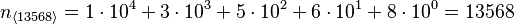
Muchos idiomas usan una base decimal (base 10), como nuestro sistema arábigo. También son comunes los sistemas vigesimales (base 20). La idea de usar un número limitado de dígitos para representar números muy grandes funciona para cualquier base b, siempre que b sea un número entero igual o mayor que 2. Las computadoras usan la base binaria (b = 2), y a veces la base octal (b = 8) o hexadecimal (b = 16).
Números en las lenguas naturales
Los idiomas usan nombres o numerales para los números, a menudo basados en el conteo con los dedos. Por eso, la mayoría de los idiomas usan sistemas de numeración en base 10 (dedos de las manos) o base 20 (dedos de manos y pies).
Véase también
 En inglés: Number Facts for Kids
En inglés: Number Facts for Kids
- Sistema de numeración
- Cifra
- Anexo:Números
- Anexo:Nombres de los números en español
|