Conjunto vacío para niños
El conjunto vacío es un concepto muy importante en las matemáticas, especialmente en la teoría de conjuntos. Imagina una caja que está completamente vacía, sin ningún objeto dentro. Eso es exactamente lo que es un conjunto vacío: una colección que no tiene ningún elemento.
Como lo único que hace que un conjunto sea único es lo que contiene, el conjunto vacío es uno solo. No puede haber dos conjuntos vacíos diferentes, porque ambos no tendrían nada. En las teorías matemáticas que usan reglas muy claras (llamadas axiomas), se acepta que el conjunto vacío existe.
Contenido
- ¿Cómo surgió la idea del conjunto vacío?
- ¿Cómo se define y se escribe el conjunto vacío?
- Propiedades importantes del conjunto vacío
- Otras características del conjunto vacío
- El conjunto vacío en otras áreas de las matemáticas
- ¿Se ha cuestionado la existencia del conjunto vacío?
- Galería de imágenes
- Véase también
¿Cómo surgió la idea del conjunto vacío?
La idea de un "conjunto vacío" es clave para entender cómo se desarrollaron las matemáticas, especialmente la teoría de conjuntos. Esta teoría nos ayuda a pensar en los números y las colecciones de una manera más formal y abstracta.
Los primeros pasos de la teoría de conjuntos
La historia del conjunto vacío se remonta al XIX. La teoría de conjuntos empezó a tomar forma con el trabajo de Georg Cantor a finales de 1800. Cantor es famoso por estudiar los tamaños de los conjuntos infinitos. Aunque él no definió el conjunto vacío directamente, sus ideas sentaron las bases para que otros lo hicieran. Cantor veía los conjuntos como colecciones de objetos y se interesaba en sus características.
La formalización del concepto
Más tarde, Richard Dedekind y Giuseppe Peano tomaron las ideas de Cantor y las usaron para definir de forma más precisa los números y el álgebra. Dedekind, por ejemplo, definió el número cero (0) como el conjunto vacío (∅). Esto fue un momento importante, ya que conectó el conjunto vacío con la idea de "nada", representando la ausencia de elementos en una colección.
Sin embargo, fue a principios del XX, con el trabajo de Ernst Zermelo y Abraham Fraenkel, cuando el conjunto vacío se convirtió en una parte fundamental de las matemáticas. Sus reglas (llamadas axiomas de Zermelo-Fraenkel o ZFC) incluyen un axioma que asegura la existencia de un conjunto sin elementos.
Importancia en las matemáticas modernas
Incluir el conjunto vacío como un objeto básico en la teoría de conjuntos tuvo un gran impacto. Es como un ladrillo fundamental para construir conjuntos más complejos. Es esencial para entender la estructura de muchos objetos matemáticos, como las funciones y las relaciones. Su utilidad se extiende a casi todas las ramas de las matemáticas, desde la lógica hasta la topología.
¿Cómo se define y se escribe el conjunto vacío?
El conjunto vacío es el conjunto que no contiene ningún elemento.
Símbolos para el conjunto vacío
El conjunto vacío se representa con los símbolos: ∅ o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \emptyset \, . Estos símbolos vienen de la letra Ø, usada en idiomas como el danés y el noruego. André Weil introdujo esta notación en 1939.
Otra forma común de escribir el conjunto vacío es usando llaves sin nada dentro:
También podemos definir el conjunto vacío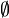 
como el conjunto de todos los elementos 
tales que 
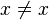. Esto significa que no hay ningún elemento que sea diferente de sí mismo, lo cual es imposible.
Propiedades importantes del conjunto vacío
Es correcto decir "el conjunto vacío" (en singular) porque es único. El conjunto vacío tiene algunas propiedades especiales:
- El único subconjunto del conjunto vacío es él mismo. Esto significa que si tienes un conjunto que es parte del conjunto vacío, ese conjunto debe ser el conjunto vacío.
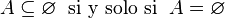
- El número de elementos (o número cardinal) del conjunto vacío es cero.
Esto significa que el conjunto vacío es un conjunto finito.
Muchas afirmaciones sobre el conjunto vacío son ciertas de forma muy sencilla, porque no tiene elementos. Por ejemplo, si decimos "todos los elementos del conjunto vacío tienen la propiedad de volar", esto es cierto porque no hay ningún elemento en el conjunto vacío que no vuele.
El conjunto vacío actúa como el "cero" en las operaciones de los conjuntos:
- Para cualquier conjunto
, el conjunto vacío es un subconjunto de .
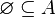
- Para cualquier conjunto , si unes con el conjunto vacío, el resultado es .
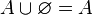
- Para cualquier conjunto , si encuentras los elementos que están tanto en como en el conjunto vacío (intersección), el resultado es el conjunto vacío.
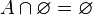
- Para cualquier conjunto , si combinas con el conjunto vacío en un producto cartesiano, el resultado es el conjunto vacío.
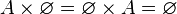
Además, el conjunto potencia (el conjunto de todos los subconjuntos) del conjunto vacío es un conjunto que contiene solo al propio conjunto vacío. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{\varnothing\} . Por lo tanto, el número de elementos de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{P}(\varnothing) es 1.
Otras características del conjunto vacío
- La intersección de un conjunto y su complemento (todo lo que no está en el conjunto) es el conjunto vacío.
- El conjunto vacío es considerado tanto un conjunto abierto como un conjunto cerrado en topología (una rama de las matemáticas).
- Si restas un conjunto de sí mismo, el resultado es el conjunto vacío.
- En probabilidad, el conjunto vacío representa un suceso imposible, y su probabilidad es 0.
El conjunto vacío en otras áreas de las matemáticas
Topología
En cualquier espacio topológico (un tipo de espacio matemático), el conjunto vacío es abierto por definición, al igual que el espacio completo. Como el complemento de un conjunto abierto es cerrado, y el conjunto vacío y el espacio completo son complementarios, el conjunto vacío también es cerrado. Esto lo convierte en un conjunto "abierto-cerrado". Además, el conjunto vacío es compacto porque todos los conjuntos finitos son compactos.
Teoría de categorías
Si es un conjunto, solo hay una forma de crear una función desde el conjunto vacío hacia . Por eso, el conjunto vacío es un "objeto inicial" único en la categoría de conjuntos y funciones.
Teoría de conjuntos
En la forma en que se construyen los números ordinales (que son una forma de contar), el número 0 se define como el conjunto vacío. Luego, los siguientes números se construyen a partir de este. Por ejemplo, 1 es el conjunto que contiene al conjunto vacío, y 2 es el conjunto que contiene al conjunto vacío y al conjunto que contiene al conjunto vacío.
¿Se ha cuestionado la existencia del conjunto vacío?
Aunque el conjunto vacío es un concepto matemático estándar y muy aceptado, a veces ha generado curiosidad y debate entre filósofos y lógicos sobre su significado.
El conjunto vacío no es "nada"
Es importante entender que el conjunto vacío no es lo mismo que "nada". Es un conjunto que no tiene nada dentro, pero un conjunto siempre es algo. Imagina una bolsa: una bolsa vacía sigue existiendo, aunque no contenga nada.
El conjunto vacío es como "el conjunto de todos los triángulos con cuatro lados", o "el conjunto de todos los números que son mayores que nueve pero menores que ocho". Estos conjuntos no tienen elementos, por lo tanto, son el conjunto vacío.
Galería de imágenes
-
El conjunto vacío es aquel que no tiene elementos.
-
Símbolo del conjunto vacío
Véase también
En inglés: Empty set Facts for Kids
