Función continua para niños
Plantilla:Ficha de concepto matemático
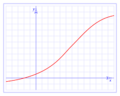
En el mundo de las matemáticas, especialmente en el cálculo, una función continua es como un camino que puedes dibujar sin levantar el lápiz del papel. Imagina que estás dibujando una línea o una curva: si puedes hacerlo de principio a fin sin interrupciones, "saltos" o "agujeros", entonces esa función es continua.
Si una función no es continua, decimos que es discontinua. Esto significa que en algún punto hay un cambio brusco, un salto o un agujero en su gráfica.
Los matemáticos han estudiado las funciones continuas durante mucho tiempo. Al principio, las entendían de forma intuitiva. Pero en el siglo XIX, lograron definir la continuidad de una manera muy precisa usando el concepto de límite.
La continuidad es una idea fundamental en el análisis matemático y en la topología, que son ramas de las matemáticas. Este artículo se centrará principalmente en las funciones que trabajan con números reales.
Contenido
¿Qué es una función continua?
Una función es continua si su gráfica no tiene interrupciones. Esto significa que si tomas dos puntos muy cercanos en el eje X (la entrada de la función), sus resultados en el eje Y (la salida de la función) también estarán muy cerca. No hay sorpresas ni cambios repentinos.
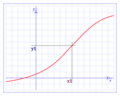
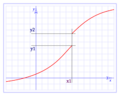
Continuidad en un punto específico
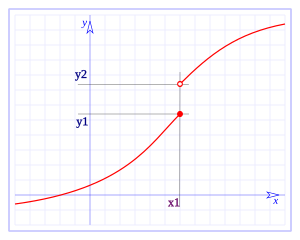
Para que una función sea continua en un punto, deben cumplirse tres cosas importantes:
- La función debe tener un valor definido en ese punto. Es decir, puedes calcular su resultado.
- El límite de la función debe existir en ese punto. Esto significa que, si te acercas al punto por la izquierda o por la derecha, la función se acerca al mismo valor.
- El valor de la función en ese punto debe ser igual al valor de su límite.
Si alguna de estas condiciones no se cumple, la función es discontinua en ese punto.
Por ejemplo, la función  no está definida en
no está definida en 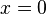 . Por lo tanto, no podemos decir que sea continua en
. Por lo tanto, no podemos decir que sea continua en 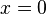 , porque no existe un valor para
, porque no existe un valor para 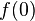 . Sin embargo, es continua en todos los demás puntos de su dominio, es decir, para cualquier número real que no sea cero.
. Sin embargo, es continua en todos los demás puntos de su dominio, es decir, para cualquier número real que no sea cero.
Continuidad en un intervalo
Una función es continua en un intervalo (un rango de números) si es continua en cada uno de los puntos que forman ese intervalo.
- Intervalo abierto (a,b): Si la función es continua en todos los puntos entre 'a' y 'b' (sin incluir 'a' ni 'b').
- Intervalo cerrado [a,b]: Si la función es continua en todos los puntos entre 'a' y 'b', y también en los puntos 'a' y 'b' mismos. Para los extremos, se considera la continuidad "lateral" (por la derecha en 'a' y por la izquierda en 'b').
Continuidad lateral
A veces, una función puede ser continua solo por un lado de un punto:
- Continua por la izquierda: Si al acercarte al punto desde la izquierda, la función se acerca al valor que tiene en ese punto.
- Continua por la derecha: Si al acercarte al punto desde la derecha, la función se acerca al valor que tiene en ese punto.
Para que una función sea continua en un punto, debe ser continua tanto por la izquierda como por la derecha en ese punto.
Ejemplos de funciones continuas
Muchas de las funciones que conoces son continuas en sus dominios:
- Funciones polinómicas: Como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = x^2 + 3x - 5 . Sus gráficas son curvas suaves sin interrupciones. La parábola es un ejemplo.
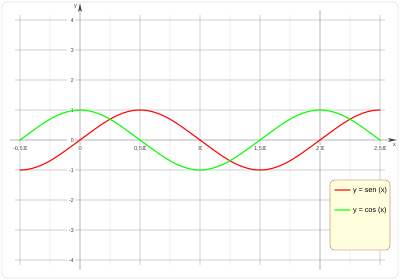
- Funciones trigonométricas: Como el seno y el coseno. Sus gráficas son ondas que se repiten sin fin.
- Funciones exponenciales: Como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = 2^x .
- Funciones logarítmicas: Como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \log(x) .
Funciones definidas por intervalos
Algunas funciones se definen con diferentes reglas para distintos rangos de números. Estas funciones, llamadas funciones definidas a trozos, pueden ser discontinuas en los puntos donde cambian las reglas.
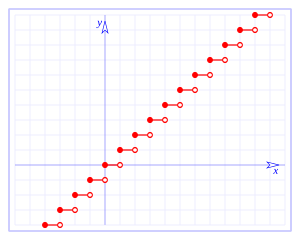
- La función parte entera (E(x)) te da el número entero más grande que es menor o igual a x. Por ejemplo, E(3.7) = 3. Su gráfica parece una escalera con "saltos" en cada número entero. Por eso, no es continua en los números enteros.
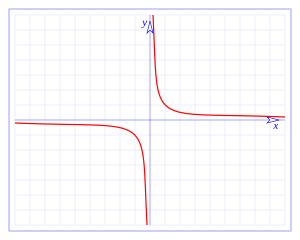
Función racional
Una función racional es una fracción donde tanto el numerador como el denominador son polinomios. Un ejemplo es  .
.
Esta función es continua en todos los números reales excepto en 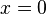 , porque no se puede dividir entre cero. Su gráfica tiene dos partes separadas, una para los números positivos y otra para los negativos, con un "salto" en el cero.
, porque no se puede dividir entre cero. Su gráfica tiene dos partes separadas, una para los números positivos y otra para los negativos, con un "salto" en el cero.
Teoremas importantes sobre funciones continuas
Las funciones continuas tienen propiedades muy interesantes que se describen en teoremas:
- Teorema de Weierstrass: Si una función es continua en un intervalo cerrado (como [a,b]), entonces siempre alcanzará un valor máximo y un valor mínimo dentro de ese intervalo.
- Teorema de Bolzano: Si una función continua cambia de signo en un intervalo (por ejemplo, empieza siendo negativa y termina siendo positiva), entonces debe haber al menos un punto en ese intervalo donde la función vale cero.
- Teorema del valor intermedio: Si una función es continua en un intervalo, y toma dos valores diferentes en los extremos de ese intervalo, entonces también tomará todos los valores que estén entre esos dos.
Derivadas y continuidad
Si una función es "derivable" en un punto (lo que significa que puedes encontrar su derivada en ese punto), entonces siempre será continua en ese punto. Piensa en la derivada como la inclinación de la curva en un punto. Si la curva tiene una inclinación definida, no puede tener un salto o un agujero.
Sin embargo, lo contrario no siempre es cierto: una función puede ser continua en un punto pero no ser derivable. Un ejemplo famoso es la función valor absoluto, 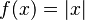 . Es continua en todas partes (puedes dibujarla sin levantar el lápiz), pero no es derivable en
. Es continua en todas partes (puedes dibujarla sin levantar el lápiz), pero no es derivable en 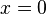 porque en ese punto su gráfica tiene un "pico" o una esquina afilada, y no una inclinación suave.
porque en ese punto su gráfica tiene un "pico" o una esquina afilada, y no una inclinación suave.
Galería de imágenes
Véase también
 En inglés: Continuous function Facts for Kids
En inglés: Continuous function Facts for Kids
- Clasificación de discontinuidades
- Lista de funciones matemáticas
- Derivación
- Continuo
- Continuidad uniforme