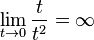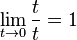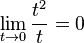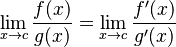Límite de una función para niños

Enciclopedia para niños

El límite de una función es una idea muy importante en las matemáticas, especialmente en el cálculo diferencial. Nos ayuda a entender qué valor toma una función cuando nos acercamos mucho a un punto específico, pero sin llegar a tocarlo.

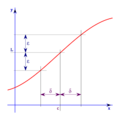
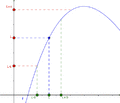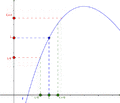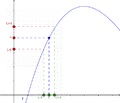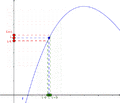
Imagina que tienes un camino (la función) y quieres saber a qué altura llegas (el valor del límite) cuando te acercas a un lugar determinado (el punto). El límite te dice esa altura, incluso si en ese lugar exacto el camino está roto o no existe. Lo importante es a dónde te diriges.

Historia del concepto de límite

Aunque la idea de límite se usó en el siglo XVII y siglo XVIII para desarrollar el cálculo, la forma en que lo escribimos hoy es más reciente.

Primeros pasos y notación

Un matemático llamado Bernard Bolzano en 1817 sentó las bases de una técnica importante para entender los límites, usando las letras griegas épsilon (ε) y delta (δ). Sin embargo, su trabajo no fue muy reconocido en su tiempo.

Más tarde, Cauchy explicó los límites en su libro Cours d'analyse en 1821, capturando la idea principal, pero no de una forma tan organizada. La primera explicación muy precisa y detallada de esta técnica la dio Karl Weierstrass entre 1850 y 1860. Desde entonces, su método se ha convertido en la forma estándar de trabajar con límites.

La forma de escribir "lim" con una flecha debajo, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{x\to c} , fue introducida por G. H. Hardy en su libro A Course of Pure Mathematics en 1908.

¿Qué es el límite de una función?

Para entender el límite de una función, piensa en una función f que se acerca a un valor L cuando la variable x se acerca a un punto c. Esto significa que podemos hacer que los valores de f(x) estén tan cerca de L como queramos, simplemente haciendo que x esté lo suficientemente cerca de c. No importa lo que pase con la función justo en el punto c.

Límite para funciones de una variable

Visualización de los parámetros utilizados en la definición de límite.

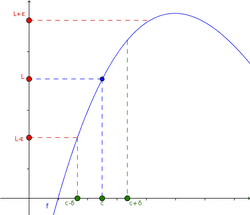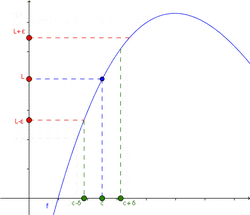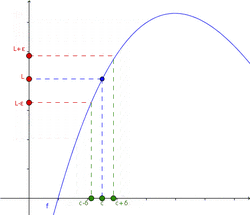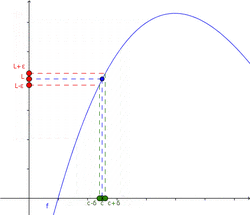
De manera sencilla, decimos que una función f tiene un límite L en un punto c si podemos hacer que f(x) esté tan cerca de L como queramos, al hacer que x esté lo suficientemente cerca de c, pero sin ser igual a c.

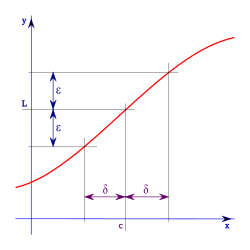
Para ser más exactos en matemáticas, usamos una definición formal. Imagina que "ε" (épsilon) es un "error" muy pequeño que queremos que tenga la función, y "δ" (delta) es una "distancia" muy pequeña alrededor del punto c.

La definición dice: El límite de una función f, cuando x se acerca a c, es L si, para cualquier "error" ε (por pequeño que sea), siempre podemos encontrar una "distancia" δ tal que, si x está a menos de δ de c (y no es c), entonces f(x) estará a menos de ε de L.

Esto se escribe así:

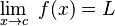\lim_{x\to c} \, \,f(x) = L

si para cada

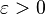\varepsilon > 0 \;

, existe un

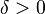\delta > 0 \;

tal que si

0 < |x-c| < \delta

entonces

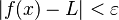|f(x)-L| < \varepsilon

Tomando valores arbitrarios de ε, podemos elegir un δ para cada uno de estos, de modo que f(x) y L se acerquen a medida que x se acerca a c.

Esta definición nos asegura que, si el límite existe, podemos acercarnos a él tanto como deseemos.

Ejemplo de cálculo de límite

Vamos a ver un ejemplo sencillo. Queremos demostrar que el límite de la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = 3x-5 cuando x se acerca a 2 es 1. 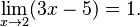$\lim_{x\to 2}(3x-5)=1.$

Para demostrarlo, si nos dan un "error" ε, debemos encontrar una "distancia" δ. Si tomamos 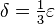$\textstyle\delta = \frac{1}{3}\varepsilon$ , podemos ver que si x está a menos de δ de 2, entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |3x-5-1| = |3x-6| = 3|x-2| . Como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |x-2| < \delta = \frac{1}{3}\varepsilon , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3|x-2| < 3 \cdot \frac{1}{3}\varepsilon = \varepsilon . Esto significa que los valores de la función 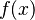$f(x)$ estarán a menos de ε de 1. ¡Así se demuestra!

Límite secuencial

Otra forma de entender el límite es pensando en sucesiones de números. Una función f tiene un límite L en un punto c si, para cualquier sucesión de números que se acerque a c, los valores de la función para esos números se acercan a L.

Esto es muy útil para demostrar que un límite no existe. Por ejemplo, si encuentras dos sucesiones que se acercan al mismo punto c, pero los valores de la función para esas sucesiones se acercan a números diferentes, entonces el límite no existe.

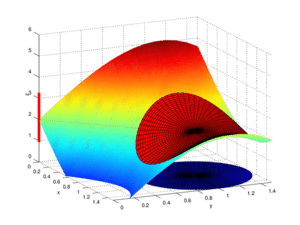
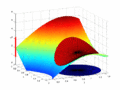
Límite para funciones de dos variables

A medida que se afina el intervalo que encierra a L puede tomarse un disco de radio δ más pequeño, dentro del cual es posible acercarse al punto (a,b), sin necesariamente pasar por él.

Las funciones pueden tener más de una variable, por ejemplo, 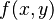$f(x,y)$ . En este caso, el límite se define de manera similar. El límite de una función f(x,y) cuando x se acerca a a e y se acerca a b es L si, para cualquier "error" ε, existe una "distancia" δ tal que si el punto (x,y) está a menos de δ del punto (a,b), entonces f(x,y) estará a menos de ε de L.

Unicidad del límite

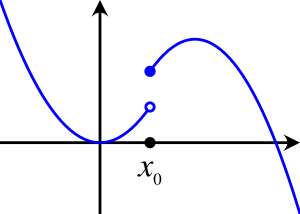
Una propiedad muy importante de los límites es que, si un límite existe, ¡es único! Esto significa que una función no puede acercarse a dos valores diferentes al mismo tiempo cuando se aproxima a un punto. Este teorema es muy útil para saber si un límite no existe.

Límites laterales

El límite cuando: x → x₀⁺ ≠ x → x₀^-. Por lo tanto, el límite cuando x → x₀ no existe.

A veces, una función se comporta de manera diferente si te acercas a un punto por la derecha o por la izquierda.

Límite por la derecha: Si te acercas a c tomando solo valores mayores que c. Se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{x \to c^+}f(x) = L^+ .
Límite por la izquierda: Si te acercas a c tomando solo valores menores que c. Se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{x \to c^-}f(x) = L^- .

Si el límite por la derecha y el límite por la izquierda son iguales, entonces decimos que el límite de la función existe en ese punto. Si son diferentes, el límite no existe. Los límites laterales son clave para entender si una función es continua o derivable en un punto.

Límites infinitos

A veces, el valor de una función puede crecer o decrecer sin límite, es decir, tender a infinito.

Cuando la variable tiende a infinito

Dado ε, puede establecerse R de modo que f(x) se «acerque» a L, a medida que x se aleja del origen ilimitadamente.

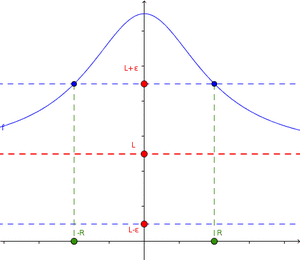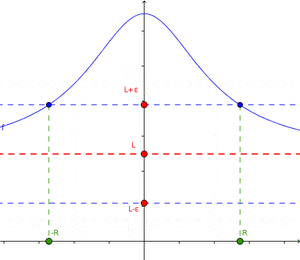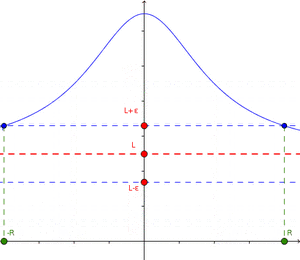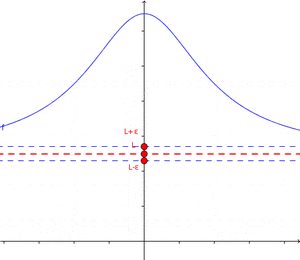
Esto ocurre cuando la variable x se hace muy, muy grande (positiva o negativa). Se escribe 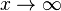$x \to\infty$ . El límite de una función f(x) cuando x tiende a infinito es L si, para cualquier "error" ε, podemos encontrar un número R tal que si x es mayor que R (en valor absoluto), entonces f(x) estará a menos de ε de L. Si este límite existe y es un número real, significa que la función tiene una asíntota horizontal.

Ejemplo de variable tendiendo a infinito

Considera la función 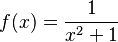$f(x)=\frac{1}{x^2+1}$ . A medida que x se hace muy grande (o muy pequeña), el valor de 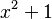$x^2+1$ se hace enorme, y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{x^2+1} se acerca a cero. 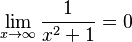$\lim_{x\to\infty} \frac{1}{x^2+1}=0$ . Esto significa que la recta $y=0$ es una asíntota horizontal para esta función.

Cuando la función tiende a infinito

Tomando R arbitrariamente grande, podemos establecer un δ de modo que cuando x se acerque a c, f(x) supere a R en valor absoluto.

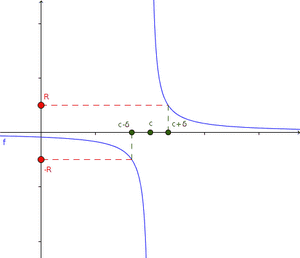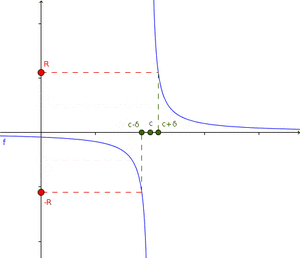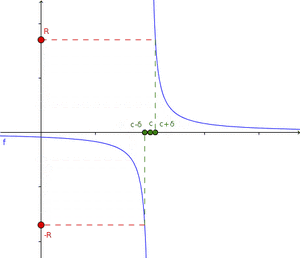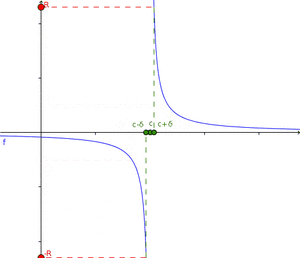
Esto sucede cuando la función crece o decrece sin límite a medida que x se acerca a un punto c. Se escribe 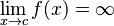$\lim_{x\to c}f(x)=\infty$ . El límite de una función f(x) cuando x tiende a c es infinito si, para cualquier número R (por grande que sea), existe una "distancia" δ tal que si x está a menos de δ de c (y no es c), entonces f(x) será mayor que R (en valor absoluto). Cuando una función tiende a infinito en un punto c, la recta vertical $x=c$ se llama asíntota vertical de la función.

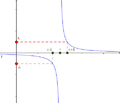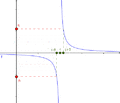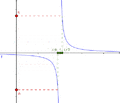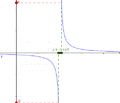
Ejemplo de función tendiendo a infinito

La función 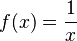$f(x)=\frac{1}{x}$ es un buen ejemplo. Cuando x se acerca a cero, los valores de $\frac{1}{x}$ se hacen muy grandes (positivos o negativos). 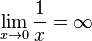$\lim_{x\to 0}\frac{1}{x}=\infty$ . La recta 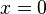$x=0$ (el eje Y) es una asíntota vertical para esta función. Es importante recordar que esto no significa que se pueda dividir por cero; simplemente describe el comportamiento de la función cerca de cero.

Cálculo de límites

Para calcular límites, usamos varias propiedades y reglas.

Propiedades generales de los límites

Si tenemos dos funciones, f(x) y g(x), y k es un número, se cumplen estas propiedades:

Límite de	Expresión
Una constante	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{x \to c} k =\, k\,
La función identidad	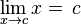$\lim_{x \to c} x = \, c \,$
El producto de una función y una constante	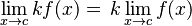$\lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,$
Una suma	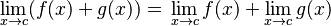$\lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,$
Una resta	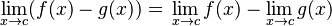$\lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,$
Un producto	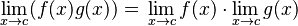$\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,$
Un cociente	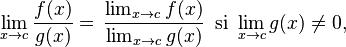$\lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,$
Una potencia	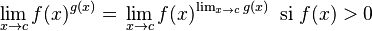${\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0$
Un logaritmo	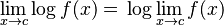${\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}$
El número e	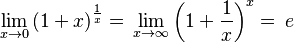${\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e$
Función f(x) acotada y g(x) infinitesimal	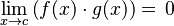${\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0$ .

Indeterminaciones

A veces, al aplicar las propiedades, obtenemos expresiones como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{0}{0} o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\infty}{\infty} . Estas se llaman indeterminaciones porque no nos dan un valor claro del límite. Necesitamos hacer más cálculos para resolverlas.

Operación	Indeterminación
Resta	$\infty - \infty$
Multiplicación	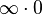$\infty \cdot 0$
División	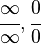$\cfrac{\infty}{\infty}, \cfrac{0}{0}$
Potencia	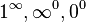$1^\infty, \infty ^0, 0^0$

Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{0}{0} es una indeterminación. No siempre da el mismo resultado:

$\lim_{t\rightarrow 0}\frac{t}{t^2}=\infty$
$\lim_{t\rightarrow 0}\frac{t}{t}=1$
$\lim_{t\rightarrow 0}\frac{t^2}{t}=0$

Para resolver estas indeterminaciones, a menudo se usan técnicas algebraicas o reglas especiales.

Regla de l'Hôpital

La Regla de l'Hôpital es una herramienta muy útil que usa las derivadas para resolver indeterminaciones de tipo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{0}{0} o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\infty}{\infty} . Dice que si tienes un límite de la forma Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{x \to c} \frac{f(x)}{g(x)} que es una indeterminación, puedes calcular el límite de las derivadas de las funciones:

$\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}$

Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{x \to 0} \frac{\sen (2x)}{\sen (3x)} = \lim_{x \to 0} \frac{2 \cos (2x)}{3 \cos (3x)} = \frac{2 \cdot 1}{3 \cdot 1} = \frac{2}{3}.

Límites trigonométricos especiales

Hay algunos límites que involucran funciones trigonométricas que son muy comunes y tienen valores específicos:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\lim_{x \to 0} {{\sen x} \over x}} =\, 1 \,
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\lim_{x \to 0} {\tan x \over x}} =\, 1 \,
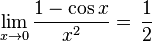
${\lim_{x \to 0} \frac {1-\cos x}{x^2} } =\, \dfrac{1}{2} \,$

El primer límite se puede demostrar usando el Teorema del emparedado (o teorema de estricción), que dice que si una función está "apretada" entre otras dos funciones que tienen el mismo límite, entonces la función del medio también tiene ese límite.

Galería de imágenes

Visualización de los parámetros utilizados en la definición de límite.
Tomando valores arbitrarios de ε, podemos elegir un δ para cada uno de estos, de modo que f(x) y L se acerquen a medida que x se acerca a c.
El límite cuando: x → x₀⁺ ≠ x → x₀^-. Por lo tanto, el límite cuando x → x₀ no existe.
Dado ε, puede establecerse R de modo que f(x) se «acerque» a L, a medida que x se aleja del origen ilimitadamente.
Tomando R arbitrariamente grande, podemos establecer un δ de modo que cuando x se acerque a c, f(x) supere a R en valor absoluto.
A medida que tomamos M cada vez más grande, podemos establecer R de modo que f supere a M en valor absoluto cuando lo hace x, con respecto a R.
A medida que se afina el intervalo que encierra a L puede tomarse un disco de radio δ más pequeño, dentro del cual es posible acercarse al punto (a,b), sin necesariamente pasar por él.

Véase también

En inglés: Limit of a function Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Límite_de_una_función&oldid=5065310»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Límite de una función para Niños. Enciclopedia Kiddle.