Adrien-Marie Legendre para niños
Datos para niños Adrien-Marie Legendre |
||
|---|---|---|
 Caricatura a la acuarela de Adrien-Marie Legendre pintada por Julien-Léopold Boilly.
|
||
| Información personal | ||
| Nacimiento | 18 de septiembre de 1752 París  Francia |
|
| Fallecimiento | 10 de enero de 1833, Auteuil, Francia |
|
| Sepultura | Cementerio de Auteuil | |
| Residencia | Francia | |
| Nacionalidad | Francia | |
| Educación | ||
| Educado en |
|
|
| Información profesional | ||
| Área | geometría; matemáticas; geodesia | |
| Conocido por | Ley de reciprocidad cuadrática, Teorema de los números primos, su libro Elementos de Geometría | |
| Cargos ocupados | Presidente de la Academia de Ciencias de Francia (1805-1806) | |
| Empleador | École Polytechnique de París | |
| Obras notables |
|
|
| Miembro de |
|
|
| Distinciones |
|
|
| Firma | ||
 |
||
Adrien-Marie Legendre (nacido el 18 de septiembre de 1752 y fallecido el 10 de enero de 1833) fue un importante matemático francés. Hizo grandes aportaciones a la estadística, la teoría de números, el álgebra abstracta y el análisis matemático. También trabajó en geodesia y fue parte de la comisión que estableció el metro como unidad de medida internacional.
Contenido
La vida de Adrien-Marie Legendre
Legendre nació en París en 1752 en una familia con buena posición económica. Estudió en el Collège Mazarin de París, donde defendió su tesis en física y matemáticas en 1770.
Sus primeros años como profesor
Entre 1775 y 1780, Legendre fue profesor de matemáticas en la Escuela Militar de París. Más tarde, desde 1795, también enseñó en la École Normale.
Durante este tiempo, Legendre participó en una comisión internacional. Esta comisión tenía la tarea de revisar los cálculos para decidir si el sistema métrico debía adoptarse.
Reconocimientos y nuevos proyectos
En 1782, la Academia de Berlín le otorgó un premio por su trabajo sobre "proyectiles en medios resistentes". Este estudio también llamó la atención de otro gran matemático, Lagrange.
El 30 de marzo de 1783, Legendre se unió a la Academia de Ciencias de Francia como ingeniero asistente, reemplazando a Laplace. En 1785, se convirtió en miembro asociado. En 1789, fue elegido Miembro de la Royal Society, una prestigiosa sociedad científica.
En 1785, basándose en los estudios de Euler, Legendre propuso una nueva idea sobre la ley de reciprocidad cuadrática. Esta idea fue demostrada más tarde por Gauss.
En 1787, fue nombrado parte de una comisión para realizar mediciones geodésicas. Su objetivo era calcular la distancia exacta entre el Observatorio de París y el Real Observatorio de Greenwich usando trigonometría. Para ello, visitó Dover y Londres en 1787.
Desafíos personales y nuevos logros
Durante la Revolución francesa, Legendre tuvo que esconderse en París y perdió su fortuna. En esta época, conoció a Margaret Couhin Claudine, con quien se casó en 1793. Margaret lo ayudó a organizar sus asuntos.
En 1795, Legendre se convirtió en uno de los seis miembros de la Sección de Matemáticas de la Academia de las Ciencias, que había sido reorganizada y renombrada como Instituto Nacional de Ciencias y Artes.
Entre 1797 y 1798, formuló el teorema de los números primos en su libro sobre teoría de números. Se cree que Gauss ya había pensado en esta idea en 1792, pero no la publicó hasta 1849.
En 1803, Napoleón Bonaparte reorganizó el Instituto Nacional, y Legendre pasó a ser miembro de la Sección de Geometría. De 1799 a 1815, trabajó como examinador de matemáticas para estudiantes que querían graduarse en artillería en la École Militaire.
Desde 1812, reemplazó a Joseph-Louis Lagrange en el Bureau des Longitudes, una institución dedicada a la astronomía y la medición del tiempo.
En 1824, a Legendre se le retiró su pensión de la École Militaire. Esto ocurrió porque se negó a votar por el candidato del gobierno en el Instituto Nacional. Su pensión fue restaurada parcialmente en 1828, cuando hubo un cambio de gobierno. En 1831, fue nombrado Oficial de la Legión de Honor, una importante distinción en Francia.
Legendre falleció en París en 1833, después de una larga enfermedad. Su esposa guardó con mucho cuidado sus pertenencias para mantener viva su memoria. Cuando ella falleció en 1856, fue enterrada junto a su esposo en el cementerio de Auteuil, el pueblo donde habían vivido.
Contribuciones científicas de Legendre
Muchas de las ideas de Legendre fueron luego desarrolladas por otros matemáticos. Por ejemplo, su trabajo sobre las raíces de polinomios inspiró la teoría de Galois. El trabajo de Abel sobre funciones elípticas se basó en los estudios de Legendre. Además, algunos avances de Gauss en estadística y teoría de números complementaron los de Legendre.
Los Elementos de Geometría
Legendre quería simplificar los Elementos de Euclides, un libro muy antiguo e importante sobre geometría. Por eso, escribió su propio libro, Elementos de Geometría, que fue un gran éxito. Tuvo 20 ediciones mientras él vivía (la primera en 1794 y la última en 1823).
En este libro, Legendre usó explicaciones cortas y claras, con las definiciones más importantes. También incluyó relaciones algebraicas en el texto. Una crítica a su libro es que usó mucho el razonamiento por reducción al absurdo, que consiste en demostrar algo mostrando que lo contrario es imposible.
La última edición de su libro fue traducida al inglés y fue muy popular en Estados Unidos durante todo el siglo XIX. Crelle lo tradujo al alemán en 1822. En Francia, otras editoriales publicaron versiones más cortas del libro.
En la Historia de la geometría, Legendre es conocido por intentar demostrar el axioma de las rectas paralelas sin éxito. No llegó a imaginar que podrían existir geometrías donde este postulado no fuera cierto. Esta idea fue desarrollada décadas después por matemáticos como Nikolái Lobachevski, Janos Bolyai y Carl Friedrich Gauss, quienes crearon las geometrías no euclidianas.
Mecánica celeste y el método de los mínimos cuadrados
Legendre enseñó durante cinco años en la Academia Militar de Francia. Allí, sus primeros trabajos se centraron en estudiar la trayectoria de los proyectiles. A partir de esto, desarrolló métodos para estudiar los cometas (1805). Fue mientras realizaba estos cálculos de mecánica celeste que ideó el método de los mínimos cuadrados.
Legendre fue el primero en publicar el método de los mínimos cuadrados, adelantándose a Gauss, quien había llegado a los mismos resultados antes, pero no los había publicado. Este método es muy útil en regresión lineal, procesamiento de señales, estadística y ajuste de curvas. Lo publicó en 1806, como un anexo a su libro sobre la "Trayectoria de los cometas".
El término "método de los mínimos cuadrados" es una traducción directa del francés "méthode des moindres carrés".
Aportes a la mecánica clásica y la aritmética
En mecánica, Legendre es conocido por la transformada de Legendre. Esta se usa para cambiar entre diferentes formas de describir el movimiento en la mecánica clásica. También se utiliza en termodinámica para calcular la entalpía a partir de otras formas de energía libre.
En 1825, completó la demostración del último teorema de Fermat para el exponente n = 5, siguiendo el trabajo de Dirichlet.
En aritmética modular, desarrolló la ley de reciprocidad cuadrática (en su libro Ensayo sobre la teoría de los números de 1798). Esta ley había sido propuesta por Euler y luego demostrada por Gauss. También fue pionero en el estudio de cómo se distribuyen los números primos y en la aplicación del análisis matemático a la teoría de números. Su idea sobre el teorema de los números primos fue demostrada rigurosamente por Hadamard y La Vallée Poussin en 1896.
Variable compleja
Alrededor de 1811, Legendre concibió la función gamma e introdujo el símbolo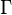 
, que se usa para generalizar el concepto de factorial a números no enteros.
Reconocimientos y honores
Además de los conceptos matemáticos que llevan su nombre, hay otros homenajes a Adrien-Marie Legendre:
- El cráter lunar Legendre fue nombrado en su honor.
- El asteroide (26950) Legendre también lleva su nombre.
- Su nombre está incluido en la lista de setenta y dos nombres de eruditos en la Torre Eiffel.
- La Calle Legendre en el XVII Distrito de París lleva su nombre desde 1865, y un pasaje cercano también.
- Fue nombrado Caballero de la Legión de Honor y miembro de la Academia de Ciencias de Francia.
El retrato equivocado
Durante dos siglos, hasta que se descubrió el error en 2009, la imagen que se usaba para representar a Adrien-Marie Legendre era en realidad la de otro francés, el político Louis Legendre (1752-1797). El error se produjo porque el retrato estaba descrito simplemente como "Legendre". El único retrato conocido de Adrien-Marie Legendre, descubierto recientemente, se encuentra en el Álbum de 73 caricaturas a la acuarela de los miembros del Instituto (1820). Esta es una colección de caricaturas de miembros de varias academias, pintadas por el artista francés Julien-Léopold Boilly.
Galería de imágenes
-
Caricaturas a la acuarela de los matemáticos franceses Adrien-Marie Legendre (izquierda) y Joseph Fourier (derecha) por el artista francés Julien-Léopold Boilly
-
Retrato del político francés Louis Legendre (1752-1797), utilizado durante casi 200 años para representar a Adrien-Marie Legendre.
.jpg)
Obras importantes
- Sur la figure des planètes (1784): Aquí aparecen por primera vez los «polinomios de Legendre».
- Éléments de géométrie (1794): Su famoso libro de geometría.
- Essai sur la théorie des nombres (1797-1798): Un ensayo sobre la teoría de los números.
- Nouvelles méthodes pour la détermination des orbites des comètes (1819): En un anexo de este libro se describe el «método de los mínimos cuadrados».
- Traité des fonctions elliptiques et intégrales Eulériennes (1826–1829): Un tratado sobre funciones elípticas.
Véase también
En inglés: Adrien-Marie Legendre Facts for Kids
- Algoritmo de Gauss-Legendre
- Constante de Legendre
- Polinomios de Legendre
- Armónicos esféricos
- Símbolo de Legendre
- Conjetura de Legendre
- Transformada de Legendre
- Joseph-Louis de Lagrange
