Cuadrado para niños
Datos para niños Cuadrado |
||
|---|---|---|
Cuadrilatero, con sus lados paralelos , y sus cuatro ángulos rectos
|
||
| Características | ||
| Tipo | Cuadrilátero, paralelogramo | |
| Lados | 4 | |
| Vértices | 4 | |
| Grupo de simetría |  |
|
| Símbolo de Schläfli | {4/1} | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Cuadrado | |
| Área |  |
|
| Ángulo interior | 90° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Un cuadrado es una figura plana muy común en geometría. Es un tipo especial de cuadrilátero, lo que significa que tiene cuatro lados. Lo que hace especial a un cuadrado es que todos sus lados miden lo mismo y todos sus ángulos interiores son rectos, es decir, miden 90 grados.
Por estas características, un cuadrado también es un rectángulo (porque tiene cuatro ángulos rectos) y un paralelogramo (porque sus lados opuestos son paralelos). Es el único polígono regular donde sus ángulos internos, centrales y externos son todos iguales (90°). Además, sus diagonales (las líneas que conectan vértices opuestos) también son todas iguales en longitud.
Contenido
¿Qué es un Cuadrado?
Un cuadrado es una figura geométrica plana. Se forma al unir cuatro puntos con líneas rectas que tienen la misma medida. Estas líneas encierran un espacio y forman cuatro esquinas perfectas, que son ángulos rectos.
Características Principales
Un cuadrilátero es un cuadrado si cumple alguna de estas condiciones:
- Es un rectángulo que tiene dos lados seguidos de la misma longitud.
- Es un rombo (una figura con cuatro lados iguales) que tiene un ángulo recto.
- Es un rombo donde todos sus ángulos son iguales.
- Es un paralelogramo con un ángulo recto y dos lados seguidos de la misma longitud.
- Es un cuadrilátero con sus cuatro lados iguales y sus cuatro ángulos iguales.
- Es un cuadrilátero donde las diagonales miden lo mismo y se cruzan formando un ángulo recto, dividiéndose por la mitad.
Propiedades Importantes
Como el cuadrado es un tipo de cuadrilátero, comparte algunas propiedades con ellos:
- Solo tiene dos diagonales.
- La suma de sus ángulos internos siempre es 360 grados.
Además, el cuadrado tiene estas propiedades únicas:
- Es un paralelogramo.
- Sus lados opuestos son siempre paralelos.
- Sus diagonales tienen la misma longitud.
- Sus diagonales se cortan justo en el centro del cuadrado.
- Sus diagonales se cruzan formando un ángulo recto.
- Sus diagonales dividen los ángulos por los que pasan exactamente por la mitad.
- Tiene cuatro ejes de simetría que pasan por su centro. Dos de ellos son perpendiculares a los lados y los otros dos son las diagonales.
Fórmulas del Cuadrado
Para calcular medidas de un cuadrado, usamos estas fórmulas:
- Si conoces la longitud de un lado (llamémosla a):
* Perímetro (la suma de todos los lados): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = 4 \cdot a * Longitud de cada diagonal: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = a \cdot \sqrt{2} * Área (el espacio que ocupa): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = a^2 (lado por lado)
- Si conoces la longitud de una diagonal (llamémosla d):
* Longitud de cada lado: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a = d \cdot \frac{\sqrt{2}}{2} * Perímetro: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = d \cdot 2 \cdot \sqrt{2} * Área: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{d^2}{2} (diagonal al cuadrado dividido por 2)
Construcciones Geométricas
- El lado de un cuadrado es igual al diámetro de la circunferencia que se puede dibujar dentro de él, tocando todos sus lados.
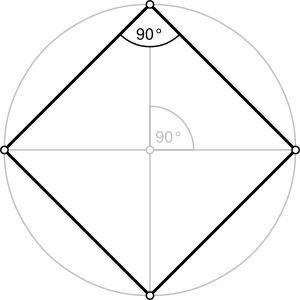
- La diagonal de un cuadrado es igual al diámetro de la circunferencia que se puede dibujar alrededor de él, pasando por todos sus vértices.
El Cuadrado Dual
Si dibujas un cuadrado dentro de otro cuadrado, uniendo los puntos medios de los lados del cuadrado exterior, obtendrás un nuevo cuadrado. Este nuevo cuadrado se llama el "dual" y su área es exactamente la mitad del área del cuadrado grande.
Datos Curiosos del Cuadrado
- Las diagonales de un cuadrado son aproximadamente 1.414 veces más largas que uno de sus lados. Este número, conocido como la raíz cuadrada de 2, fue el primer número que se descubrió que era irracional (no se puede escribir como una fracción simple).
- Un cuadrado tiene un área más grande que cualquier otro cuadrilátero que tenga el mismo perímetro.
- Los mosaicos cuadrados son una de las tres formas regulares que pueden cubrir una superficie plana sin dejar huecos ni superponerse. Las otras dos son los triángulos equiláteros y los hexágonos regulares.
- Un cuadrado es una figura muy simétrica. Tiene cuatro líneas de simetría de reflexión (puedes doblarlo por esas líneas y las dos mitades coincidirán) y puede girarse 90, 180 o 270 grados y seguir viéndose igual.
Coordenadas de un Cuadrado
En un plano de coordenadas, si un cuadrado tiene sus lados verticales y horizontales y está centrado en el punto (0,0), sus vértices pueden estar en puntos como (1,1), (-1,1), (-1,-1) y (1,-1).
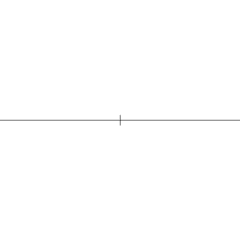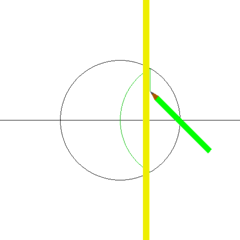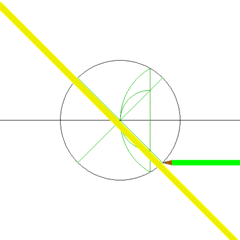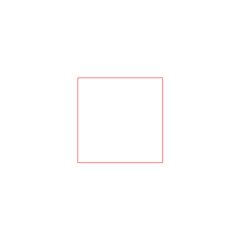
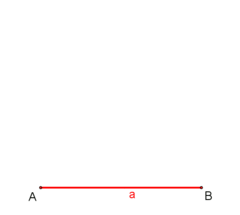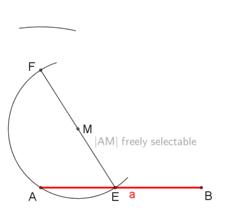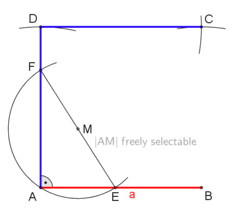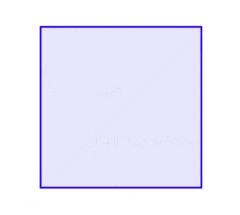
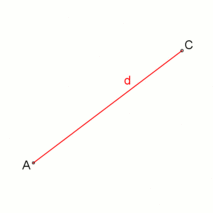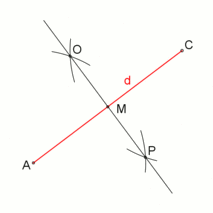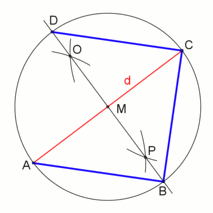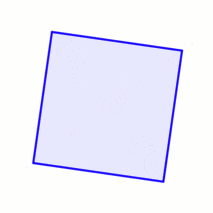
Cómo Construir un Cuadrado
Las siguientes animaciones muestran cómo puedes dibujar un cuadrado usando solo una regla y un compás. Esto es posible porque el número 4 (el número de lados de un cuadrado) es una potencia de dos.
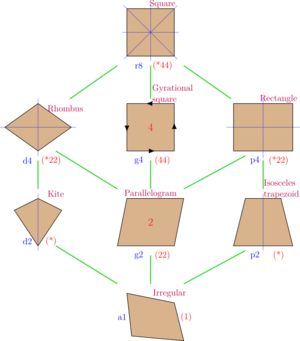
Simetría del Cuadrado
El cuadrado tiene una alta simetría. Esto significa que puedes moverlo (girarlo o voltearlo) de varias maneras y seguirá luciendo exactamente igual. Tiene simetría de rotación (puedes girarlo 90, 180 o 270 grados y se verá igual) y simetría de reflexión (puedes doblarlo por la mitad de varias maneras y las dos mitades coincidirán).
Un cuadrado es un caso especial de otras figuras con menos simetría, como:
- Un rectángulo con dos lados adyacentes iguales.
- Un rombo con un ángulo recto.
- Un paralelogramo con un ángulo recto y dos lados adyacentes iguales.
Cuadrados dentro de Triángulos
Casi todos los triángulos (aquellos con todos sus ángulos menores de 90 grados) pueden tener tres cuadrados "inscritos" dentro de ellos. Esto significa que los cuatro vértices del cuadrado tocan los lados del triángulo.
- En un triángulo rectángulo (con un ángulo de 90 grados), dos de estos cuadrados son iguales y tienen un vértice en el ángulo recto del triángulo.
- Un triángulo obtuso (con un ángulo mayor de 90 grados) solo tiene un cuadrado inscrito, cuyo lado coincide con la parte más larga del lado mayor del triángulo.
El área que ocupa el cuadrado dentro del triángulo nunca es más de la mitad del área total del triángulo.
La Cuadratura del Círculo
La cuadratura del círculo es un problema muy antiguo de la geometría. Los antiguos geómetras querían saber si era posible construir un cuadrado que tuviera exactamente la misma área que un círculo dado, usando solo una regla y un compás en un número limitado de pasos.
En 1882, se demostró que esta tarea es imposible. Esto se debe a que el número π (pi), que es fundamental para calcular el área de un círculo, es un tipo de número que no se puede construir con regla y compás.
Geometría No Euclidiana
En la geometría no euclidiana, que es diferente de la geometría que aprendemos normalmente, los cuadrados también tienen 4 lados y ángulos iguales, pero su forma puede variar:
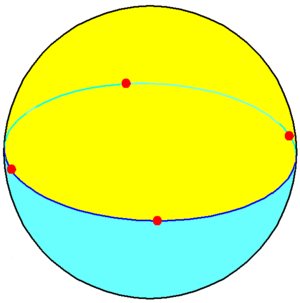
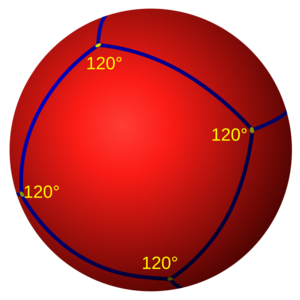
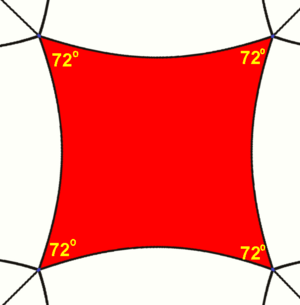
- En la geometría esférica (como la superficie de una pelota), un cuadrado tiene lados que son arcos de círculo y sus ángulos son mayores de 90 grados. Cuanto más grande es el cuadrado esférico, más grandes son sus ángulos.
- En la geometría hiperbólica, los cuadrados tienen ángulos menores de 90 grados. Cuanto más grande es el cuadrado hiperbólico, más pequeños son sus ángulos.
Cuadrado Cruzado
Un cuadrado cruzado es una figura que se forma a partir de un cuadrado, pero sus líneas se cruzan. Imagina que tomas un cuadrado, quitas dos lados opuestos y luego conectas los vértices con sus diagonales. Se parece a una pajarita o una mariposa.
Un cuadrado y un cuadrado cruzado comparten algunas propiedades:
- Sus lados opuestos tienen la misma longitud.
- Sus dos diagonales tienen la misma longitud.
- Tienen dos líneas de simetría de reflexión y simetría de rotación de 180 grados.
|
Véase también
 En inglés: Square Facts for Kids
En inglés: Square Facts for Kids