Función trigonométrica inversa para niños

Enciclopedia para niños

Datos para niños Trigonometría

Referencias
Constantes exactas ·Tablas ·Circunferencia goniométrica
Funciones, leyes y teoremas
Funciones e (inversas) ·Senos ·Cosenos ·Tangentes ·Cotangentes ·Teorema de Pitágoras·Identidades y fórmulas de trigonometría
Cálculo infinitesimal
Sustitución trigonométrica ·Integrales de funciones directas (e inversas) ·Derivadas
Temas relacionados
Temas ·Historia ·Usos·Trigonometría generalizada

En matemáticas, las funciones trigonométricas inversas son herramientas especiales que nos ayudan a encontrar el ángulo cuando ya conocemos el valor de una función trigonométrica (como el seno o el coseno) de ese ángulo. Imagina que sabes la altura de una escalera apoyada en una pared y la distancia de su base a la pared. Con las funciones trigonométricas inversas, puedes calcular el ángulo que forma la escalera con el suelo.

Estas funciones son las inversas de las seis funciones trigonométricas principales: seno, coseno, tangente, cosecante, secante y cotangente. Se usan mucho en campos como la ingeniería, la navegación, la física y la geometría.

Contenido

¿Cómo se escriben?
Propiedades importantes
Aplicaciones de las funciones trigonométricas inversas
- Encontrar el ángulo de un triángulo rectángulo
- En informática e ingeniería
  - La función atan2
Galería de imágenes
Véase también

¿Cómo se escriben?

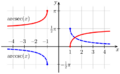
Existen varias formas de escribir las funciones trigonométricas inversas. La más común es usar el prefijo "arco", como:

$arcsin(x)$ para el arco seno.
$arccos(x)$ para el arco coseno.
$arctan(x)$ para el arco tangente.

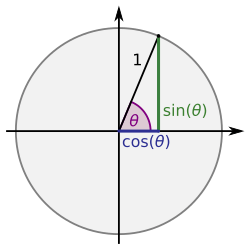
Esta forma de escribir viene de la idea de un circunferencia goniométrica (un círculo con radio 1). En este círculo, la longitud de un arco es igual a la medida del ángulo en radianes. Así, "el arco cuyo coseno es x" es lo mismo que "el ángulo cuyo coseno es x".

En los programas de computadora, a menudo verás estas funciones abreviadas como `asin`, `acos` y `atan`.

También se usa a veces la notación con un pequeño "menos uno" como exponente, por ejemplo, $sin -1 (x)$ . Esta notación fue introducida por John Herschel en 1813. Aunque es correcta para indicar una función inversa, a veces puede confundirse con elevar a la potencia de -1 (el inverso multiplicativo). Para evitar confusiones, el estándar ISO 80000-2 recomienda usar solo el prefijo "arco".

Propiedades importantes

Valores principales de las funciones inversas

Las funciones trigonométricas normales (seno, coseno, etc.) repiten sus valores. Por ejemplo, el seno de 0 grados es 0, pero también el seno de 180 grados es 0, y el seno de 360 grados es 0. Para que las funciones inversas nos den un único ángulo, necesitamos "restringir" sus valores a un rango específico. A este rango se le llama el "valor principal".

La siguiente tabla muestra los valores principales más comunes para cada función trigonométrica inversa:

Nombre	Notación	Definición	Valores de x (entrada)	Rango de ángulos (radianes)	Rango de ángulos (grados)
arco seno	$y = arcsen(x)$	$x = sen (y)$	−1 ≤ x ≤ 1	−π/2 ≤ y ≤ π/2	−90° ≤ y ≤ 90°
arco coseno	$y = arccos(x)$	$x = cos (y)$	−1 ≤ x ≤ 1	0 ≤ y ≤ π	0° ≤ y ≤ 180°
arco tangente	$y = arctan(x)$	$x = tan (y)$	todos los números reales	−π/2 < y < π/2	−90° < y < 90°
arco cotangente	$y = arccot(x)$	$x = cot (y)$	todos los números reales	0 < y < π	0° < y < 180°
arco secante	$y = arcsec(x)$	$x = sec (y)$	x ≥ 1 o x ≤ -1	0 ≤ y < π/2 o π/2 < y ≤ π	0° ≤ y < 90° o 90° < y ≤ 180°
arco cosecante	$y = arccsc(x)$	$x = csc (y)$	x ≤ −1 o 1 ≤ x	−π/2 ≤ y < 0 o 0 < y ≤ π/2	−90° ≤ y < 0° o 0° < y ≤ 90°

Relaciones entre funciones trigonométricas y sus inversas

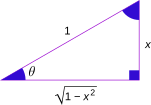
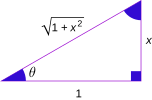
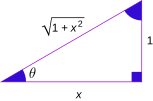
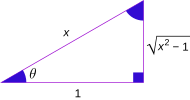
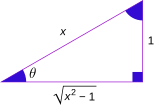
Podemos encontrar relaciones entre las funciones trigonométricas y sus inversas usando un triángulo rectángulo. Si un lado mide 1 y otro lado mide x, podemos usar el teorema de Pitágoras para encontrar el tercer lado. Luego, aplicamos las definiciones de seno, coseno, etc.

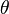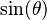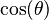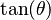$\theta$	$\sin(\theta)$	$\cos(\theta)$	$\tan(\theta)$
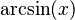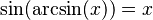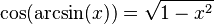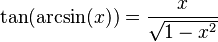$\arcsin(x)$	$\sin(\arcsin(x)) = x$	$\cos(\arcsin(x)) = \sqrt{1-x^2}$	$\tan(\arcsin(x)) = \frac{x}{\sqrt{1-x^2}}$
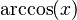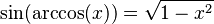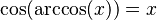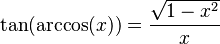$\arccos(x)$	$\sin(\arccos(x)) = \sqrt{1-x^2}$	$\cos(\arccos(x)) = x$	$\tan(\arccos(x)) = \frac{\sqrt{1-x^2}}{x}$
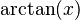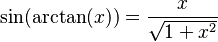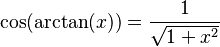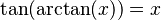$\arctan(x)$	$\sin(\arctan(x)) = \frac{x}{\sqrt{1+x^2}}$	$\cos(\arctan(x)) = \frac{1}{\sqrt{1+x^2}}$	$\tan(\arctan(x)) = x$
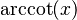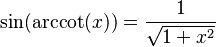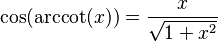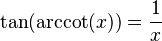$\arccot(x)$	$\sin(\arccot(x)) = \frac{1}{\sqrt{1+x^2}}$	$\cos(\arccot(x)) = \frac{x}{\sqrt{1+x^2}}$	$\tan(\arccot(x)) = \frac{1}{x}$
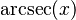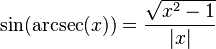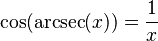$\arcsec(x)$	$\sin(\arcsec(x)) = \frac{\sqrt{x^2-1}}{\|x\|}$	$\cos(\arcsec(x)) = \frac{1}{x}$	$\tan(\arcsec(x)) = \sgn(x)\sqrt{x^2-1}$
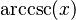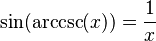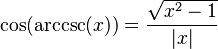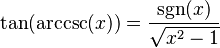$\arccsc(x)$	$\sin(\arccsc(x)) = \frac{1}{x}$	$\cos(\arccsc(x)) = \frac{\sqrt{x^2-1}}{\|x\|}$	$\tan(\arccsc(x)) = \frac{\sgn(x)}{\sqrt{x^2-1}}$

Relaciones entre las funciones trigonométricas inversas

Las funciones trigonométricas inversas también tienen relaciones entre sí. Por ejemplo:

Ángulos complementarios:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arccos(x) = \frac{\pi}{2} - \arcsin(x)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arccot(x) = \frac{\pi}{2} - \arctan(x)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arccsc(x) = \frac{\pi}{2} - \arcsec(x)

Argumentos negativos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arcsin(-x) = -\arcsin(x)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arccos(-x) = \pi -\arccos(x)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arctan(-x) = -\arctan(x)

Aplicaciones de las funciones trigonométricas inversas

Encontrar el ángulo de un triángulo rectángulo

Triángulo rectángulo

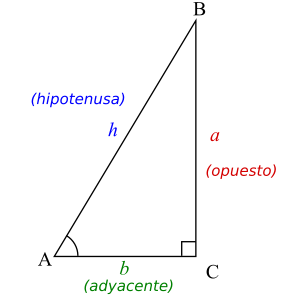
Las funciones trigonométricas inversas son muy útiles para encontrar los ángulos de un triángulo rectángulo si conoces las longitudes de sus lados.

Por ejemplo, si conoces el lado opuesto y la hipotenusa, puedes usar el arco seno:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta = \arcsin \left( \frac{\text{opuesto}}{\text{hipotenusa}} \right)

Si conoces el lado adyacente y la hipotenusa, puedes usar el arco coseno:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta = \arccos \left( \frac{\text{adyacente}}{\text{hipotenusa}} \right)

A menudo, la hipotenusa no se conoce. En ese caso, el arco tangente es muy útil porque solo necesita los lados opuesto y adyacente:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta = \arctan \left( \frac{\text{opuesto}}{\text{adyacente}} \right)

Ejemplo: Imagina que un techo baja 8 metros por cada 20 metros que se extiende horizontalmente. Para saber el ángulo θ que forma el techo con la horizontal, puedes usar el arco tangente:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta = \arctan \left( \frac{8}{20} \right) \approx 21.8^{\circ}

En informática e ingeniería

La función atan2

La función atan2 es una versión especial del arco tangente que se usa mucho en computación y robótica. A diferencia del `arctan` normal, `atan2(y, x)` toma dos valores (y y x) y puede determinar el ángulo en cualquier cuadrante de un plano, dando un resultado entre -180° y 180° (o -π y π radianes). Esto es muy útil para saber la dirección exacta de un punto en un mapa o en un juego.

Por ejemplo, si un punto está en (-1, 1), `atan2(1, -1)` te daría 135° (o 3π/4 radianes), mientras que un `arctan(1/-1)` normal solo te daría -45° (o -π/4 radianes), sin indicar el cuadrante correcto.

Galería de imágenes

Los valores principales habituales de las funciones arcsin (x) (rojo) y arccos (x) (azul) representados en el plano cartesiano
Los valores principales habituales de las funciones arctan (x) (rojo) y arccot (x) (azul) representados en el plano cartesiano
Los valores principales habituales de las funciones arcsec (x) (rojo) y arccsc (x) (azul) representados en el plano cartesiano

Véase también

En inglés: Trigonometric function Facts for Kids

Identidades y fórmulas de trigonometría
Función trigonométrica

Obtenido de «https://ninos.kiddle.co/index.php?title=Función_trigonométrica_inversa&oldid=4969687»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Función trigonométrica inversa para Niños. Enciclopedia Kiddle.