Grado sexagesimal para niños
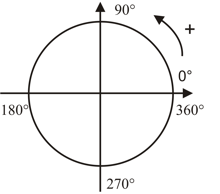
Un grado sexagesimal (símbolo °) es una unidad que usamos para medir ángulos. Imagina un círculo completo; un grado sexagesimal es una parte muy pequeña de ese círculo, exactamente la parte 1/360 de una vuelta completa. También es la parte 1/90 de un ángulo recto (que es como la esquina de un cuadrado).
Contenido
¿Por qué 360 grados?
No estamos completamente seguros de por qué se eligió el número 360 para dividir el círculo, pero hay algunas ideas interesantes:
El año y los calendarios antiguos
Una teoría dice que está relacionado con el número de días que tiene un año. Los antiguos astrónomos notaron que el sol parece moverse aproximadamente un grado cada día en su recorrido por el cielo. Algunos calendarios antiguos, como el persa y el babilónico, usaban 360 días para un año. Esto podría estar conectado con el uso de un sistema de números basado en 60.
El sistema de números de base 60

Otra idea es que los babilonios, que usaban un sistema de números basado en 60 (llamado sexagesimal), dividieron el círculo usando el ángulo de un triángulo equilátero como base. Luego, lo subdividieron en 60 partes, siguiendo su sistema numérico. La primera trigonometría, usada por los astrónomos babilonios y luego por los griegos, se basaba en la cuerda de un círculo. Una cuerda del mismo tamaño que el radio del círculo era una medida natural. Una sexagésima parte de esta medida, usando sus divisiones de base 60, se convirtió en un grado.

Científicos griegos como Aristarco de Samos e Hiparco de Nicea fueron de los primeros en usar las ideas de los babilonios. Ellos, junto con otros como Arquímedes, dividieron el círculo en 360 grados, y cada grado en 60 minutos de arco.
Un número muy divisible
Una razón muy práctica para elegir 360 es que es un número que se puede dividir fácilmente por muchos otros números. El 360 tiene 24 divisores (números que lo dividen sin dejar resto), lo que lo hace muy útil para dividir un círculo en partes iguales. Por ejemplo, se puede dividir por 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 y 360. Esto es muy útil para cosas como dividir el mundo en 24 zonas horarias, donde cada una es de 15° de longitud.
Es posible que todas estas razones hayan influido en la elección del 360.
¿Cómo se definen los grados?
El grado sexagesimal es parte de un sistema para medir ángulos. Así es como se define:
- Un ángulo recto (como la esquina de una mesa) mide 90° (grados sexagesimales).
- 1 grado sexagesimal (1°) se divide en 60′ (minutos sexagesimales).
- 1 minuto sexagesimal (1′) se divide en 60″ (segundos sexagesimales).
Este sistema de base 60 viene de la antigua Mesopotamia, donde los astrónomos y matemáticos lo usaban para sus cálculos.
Cómo se escriben los ángulos
Podemos escribir un ángulo usando grados, minutos y segundos. Si hay partes más pequeñas que un segundo, se escriben como decimales de segundo.
- Ejemplos: 12°34′34″, 13°3′23,8″, 124°45′34,70″, -2°34′10″.
Es importante no dejar espacios entre los números y los símbolos (por ejemplo, 12°34′34″, no 12° 34′ 34″).
También podemos convertir un ángulo a una forma decimal, solo con grados:
- 1′ (minuto) es igual a (1/60)° (aproximadamente 0,01666667°).
- 1″ (segundo) es igual a (1/60)′ o (1/3600)° (aproximadamente 0,00027778°).
Así, 12°15′23″ es aproximadamente 12,25639°.
Notación decimal
También podemos expresar un ángulo solo con grados y decimales.
- Ejemplos: 23,2345°, 12,32°, -50,265°, 123,696°.
Otras formas de medir ángulos
Además de los grados, hay otras unidades para medir ángulos:
Radianes
En matemáticas más avanzadas, los ángulos a menudo se miden en radianes. Esto se debe a que las fórmulas matemáticas son más sencillas cuando se usan radianes. Un giro completo (360°) es igual a 2π radianes. Así, 180° es igual a π radianes.
Gradianes o gones
Cuando se inventó el sistema métrico, hubo un intento en Francia de reemplazar los grados por "grados" decimales. En este sistema, un ángulo recto era de 100 gon, y un círculo completo era de 400 gon. Aunque esta idea no se usó mucho, algunas calculadoras científicas todavía los incluyen.
Milésimas angulares
Esta unidad se usa principalmente en aplicaciones militares. Hay varias versiones, pero suelen ser aproximadamente 1/6000 de una vuelta completa.
Relación entre radianes y grados
Sabemos que una circunferencia completa tiene 360° y también 2π radianes. Esto nos permite convertir entre ellos:
- 360 grados = 2π radianes
- 180 grados = π radianes
Para convertir grados (g) a radianes (r): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r = g \cdot \frac{\pi}{180}
Para convertir radianes (r) a grados (g): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g = r \cdot \frac{180}{\pi}
Diferencias entre radián, gradián y grado sexagesimal
Las tres son unidades para medir ángulos, pero se definen de forma diferente:
- Radián (rad): Es el ángulo en el centro de un círculo que abarca un arco de la misma longitud que el radio del círculo.
- Gradián o grado centesimal (g): Es la parte 1/400 de una circunferencia completa.
- Grado sexagesimal (°): Es la parte 1/360 de una circunferencia completa.
Conversión de ángulos comunes
| Revolución | Radian | Grado sexagesimal |
Gradián | Miliradián | Puntos del compás | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0 de circulo | 0 rad | 0° | 0g | 0 mrad | 0 pt | ||||
| 172 de circulo | π36 rad | 𝜏72 rad | ≈ 0,08727 rad | 5° | 509g | 250π9 mrad | 125𝜏9 mrad | ≈ 87,266 mrad | 49 pt |
| 124 de circulo | π12 rad | 𝜏24 rad | ≈ 0,2618 rad | 15° | 503g | 250π3 mrad | 125𝜏3 mrad | ≈ 261,799 mrad | 43 pt |
| 116 de circulo | π8 rad | 𝜏16 rad | ≈ 0,3927 rad | 22,5° o 22°30′ | 25g | 125π mrad | 125𝜏2 mrad | ≈ 392,699 mrad | 2 pt |
| 112 de circulo | π6 rad | 𝜏12 rad | ≈ 0,5236 rad | 30° | 1003g | 500π3 mrad | 250𝜏3 mrad | ≈ 523,599 mrad | 83 pt |
| 110 de circulo | π5 rad | 𝜏10 rad | ≈ 0,6283 rad | 36° | 40g | 200π mrad | 100𝜏 mrad | ≈ 628,319 mrad | 165 pt |
| 18 de circulo | π4 rad | 𝜏8 rad | ≈ 0,7854 rad | 45° | 50g | 250π mrad | 125𝜏 mrad | ≈ 785,398 mrad | 4 pt |
| 12π de circulo | 1 rad | 180π° | 200πg | 1000 mrad | 16π pt | ||||
| 16 de circulo | π3 rad | 𝜏6 rad | ≈ 1,047 rad | 60° | 2003g | 1000π3 mrad | 500𝜏3 mrad | ≈ 1047,198 mrad | 163 pt |
| 15 de circulo | 2π5 rad | 𝜏5 rad | ≈ 1,257 rad | 72° | 80g | 400π mrad | 200𝜏 mrad | ≈ 1256,637 mrad | 325 pt |
| 14 de circulo | π2 rad | 𝜏4 rad | ≈ 1,571 rad | 90° | 100g | 500π mrad | 250𝜏 mrad | ≈ 1570,796 mrad | 8 pt |
| 13 de circulo | 2π3 rad | 𝜏3 rad | ≈ 2,094 rad | 120° | 4003g | 2000π3 mrad | 1000𝜏3 mrad | ≈ 2094,395 mrad | 323 pt |
| 25 de circulo | 4π5 rad | 2𝜏5 rad | ≈ 2,513 rad | 144° | 160g | 800π mrad | 400𝜏 mrad | ≈ 2513,274 mrad | 645 pt |
| 12 de circulo | π rad | 𝜏2 rad | ≈ 3,142 rad | 180° | 200g | 1000π mrad | 500𝜏 mrad | ≈ 3141,593 mrad | 16 pt |
| 34 de circulo | 3π2 rad | 3𝜏4 rad | ≈ 4,712 rad | 270° | 300g | 1500π mrad | 750𝜏 mrad | ≈ 4712,389 mrad | 24 pt |
| 1 circulo | 2π rad | 𝜏 rad | ≈ 6,283 rad | 360° | 400g | 2000π mrad | 1000𝜏 mrad | ≈ 6283,185 mrad | 32 pt |
Características especiales del número 360
Como ya mencionamos, el 360 es un número muy especial porque tiene muchos divisores. Esto significa que un círculo dividido en 360 grados se puede dividir en muchas secciones iguales y enteras. Los 24 divisores de 360 son: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360.
Uso legal y en el Sistema Internacional
Aunque el grado sexagesimal no es parte del Sistema Internacional de Unidades (SI), se permite su uso junto con las unidades del SI. En algunos países, como Suiza, el grado sexagesimal es una unidad de medida legal.
|
Véase también
 En inglés: Degree (angle) Facts for Kids
En inglés: Degree (angle) Facts for Kids