Apolonio de Perge para niños
Datos para niños Apolonio de Perga(Griego antiguo: Ἀπολλώνιος) |
||
|---|---|---|
 Detalle de una obra de 1537 representanto a Apolonio de Perge
|
||
| Información personal | ||
| Nombre de nacimiento | Ἀπολλώνιος | |
| Nombre en griego antiguo | Ἀπολλώνιος ὁ Περγαῖος | |
| Nacimiento | 262 a. C. Perge |
|
| Fallecimiento | 190 a. C. Alejandría |
|
| Información profesional | ||
| Área | Matemático y Astrónomo | |
| Conocido por | Teoría de los epiciclos Problema de Apolonio |
|
| Obras notables |
|
|
Apolonio de Perga (en griego Ἀπολλώνιος) fue un importante matemático y astrónomo de la Antigua Grecia. Nació alrededor del año 262 a.C. en Perge (hoy Turquía) y falleció cerca del 190 a.C. en Alejandría (Egipto).
Es muy conocido por su libro Sobre las secciones cónicas. Fue él quien les dio los nombres de elipse, parábola e hipérbola a estas figuras geométricas. También encontró una forma de resolver ecuaciones complejas usando la geometría.
Apolonio también propuso la idea de las órbitas excéntricas o la teoría de los epiciclos. Esto ayudaba a explicar cómo se movían los planetas en el cielo y por qué la Luna parecía cambiar de velocidad. Sus trabajos sobre geometría fueron tan importantes que lo llamaron El Gran Geómetra.
Contenido
Biografía de Apolonio de Perga
¿Cuándo y dónde vivió Apolonio?
Apolonio nació en la ciudad de Perge, que hoy forma parte de Turquía, alrededor del año 262 a.C. Murió en Alejandría, Egipto, cerca del año 190 a.C.
Se sabe que vivió durante los reinados de varios reyes Ptolomeos en Egipto. Era más joven que el famoso Arquímedes, otro gran matemático. Apolonio estudió y enseñó en Alejandría, una ciudad muy importante para el conocimiento en la antigüedad.
Las Contribuciones de Apolonio a las Matemáticas
¿Qué descubrió Apolonio sobre las secciones cónicas?
Apolonio estudió a fondo las secciones cónicas. Estas son las formas que se obtienen al cortar un cono con un plano. Él usó proporciones para entender las propiedades de la parábola, la elipse y la hipérbola.
También propuso y resolvió un famoso desafío matemático llamado el problema de Apolonio. Este problema consiste en encontrar una circunferencia que toque a otras tres figuras dadas (pueden ser puntos, rectas o circunferencias). Este trabajo estaba en su libro Las Tangencias, que lamentablemente se perdió.
¿Cuáles fueron las obras más importantes de Apolonio?
Apolonio escribió muchos libros, pero la mayoría se han perdido. Solo dos de sus obras han llegado hasta nosotros: Secciones en una razón dada (solo en árabe) y Las Cónicas. Esta última es su obra más famosa y una de las más importantes en la historia de las matemáticas, junto con los Elementos de Euclides.
Las Cónicas tiene ocho libros. En ellos, Apolonio explica las propiedades de las secciones cónicas, cómo se cortan entre sí y cómo se pueden usar para resolver problemas.
- El libro I: Explica las propiedades básicas de estas curvas.
- El libro II: Habla de los diámetros y las líneas tangentes de las curvas.
- El libro III: Describe los diferentes tipos de conos.
- El libro IV: Muestra cómo se pueden cortar las secciones de los conos.
- El libro V: Estudia los segmentos más largos y más cortos en relación con una cónica.
- El libro VI: Trata sobre cónicas que son similares entre sí.
- El libro VII: Se enfoca en los diámetros conjugados.
- El libro VIII: Se perdió, pero se cree que era un resumen o un apéndice.
Los métodos de Apolonio, como usar líneas para establecer sistemas de referencia, son muy parecidos a los que se usan en la Geometría analítica moderna. De hecho, él ya usaba algo similar a las coordenadas rectangulares. Con ellas, definió las ecuaciones de la parábola, la hipérbola y la elipse.
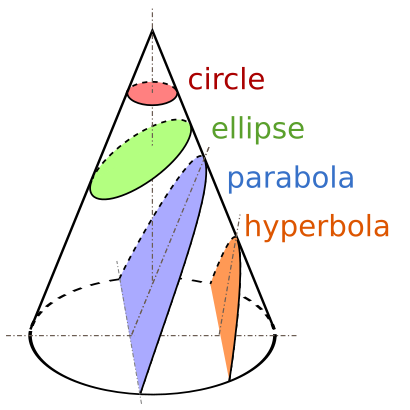
¿Cómo se forman las secciones cónicas?
Una superficie cónica se forma al girar una línea recta alrededor de un punto fijo. Un cono es una parte de esta superficie.
Una "sección transversal" es el corte que se hace a un cono con un plano.
- Si el plano pasa por el vértice del cono, la sección es un triángulo.
- Si el plano es paralelo a la base del cono, la sección es una circunferencia.
- La elipse se forma cuando el plano corta el cono de forma inclinada, pero sin ser paralelo a un lado del cono.
- La parábola se forma cuando el plano es paralelo a uno de los lados del cono.
- La hipérbola se forma cuando el plano es paralelo al eje del cono y corta ambas partes del cono, creando dos curvas separadas.
Los matemáticos griegos usaban estas figuras en ingeniería y arquitectura. Apolonio ayudó a que la geometría se acercara al álgebra geométrica griega, donde se usaban segmentos de línea como si fueran variables.
Reconocimientos a Apolonio
- El cráter lunar Apollonius fue nombrado en su honor.
Véase también
 En inglés: Apollonius of Perga Facts for Kids
En inglés: Apollonius of Perga Facts for Kids
- Problema de Apolonio
Galería de imágenes
-
Edición de 1654 de Las Cónicas editada por Francesco Maurolico




