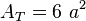Cubo para niños

Datos para niños Cubo
Familia: sólidos platónicos
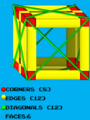
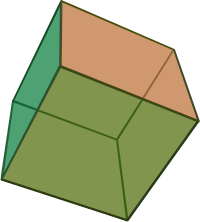Imagen del sólido
Caras	6
Aristas	12
Vértices	8
Grupo de simetría	Octaédrico (Oh)
Poliedro dual	Octaedro

Un cubo o hexaedro regular es una figura geométrica tridimensional. Está formado por seis caras que son cuadrados iguales. Es uno de los sólidos platónicos, que son formas especiales con caras, aristas y vértices regulares.

Además de ser un hexaedro (una figura con seis caras), un cubo también se puede ver como un paralelepípedo recto y rectangular. Esto significa que todas sus caras son cuadradas y están en pares paralelos. También es un prisma recto, donde la base es un cuadrado y su altura es igual al lado de la base.

El cubo cumple con el teorema de Euler para poliedros, que dice que el número de caras (C) más el número de vértices (V) es igual al número de aristas (A) más dos. Para un cubo, esto es 6 caras + 8 vértices = 12 aristas + 2 (14 = 14).

El cubo es el dual del octaedro. Esto significa que si conectas los centros de las caras de un cubo, formas un octaedro. El cubo tiene una simetría especial llamada cúbica u octaédrica. Es el único poliedro convexo (que no tiene "huecos" ni "curvas hacia adentro") cuyas caras son todas cuadradas.

¿Cómo se ve un cubo desde diferentes ángulos?

El cubo tiene cuatro formas especiales de verse si lo proyectamos en un plano. Estas proyecciones se centran en un vértice, una arista, una cara o son normales a su figura de vértice.

Proyecciones ortogonales

Centrado en	Cara	Vértice
Planos de Coxeter	B2	A2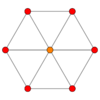
Proyectiva simetría	[4]	[6]
Vistas inclinadas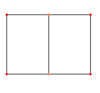

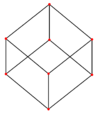Cubo esférico: ¿Cómo se ve en una esfera?

Un cubo también se puede dibujar en la superficie de una esfera. Luego, se puede proyectar esa imagen de la esfera a un plano usando una proyección estereográfica. Esta proyección mantiene los ángulos, pero cambia las áreas y las longitudes. Las líneas rectas de la esfera se ven como arcos de círculo en el plano.

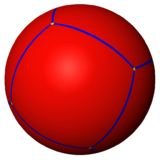Proyección ortográfica	Proyección estereográfica

¿Cómo se ubica un cubo en el espacio?

Coordenadas cartesianas de un cubo

Imagina un cubo en un sistema de coordenadas. Si el centro del cubo está en el punto (0,0,0) y sus lados miden 2 unidades, los puntos de sus esquinas (vértices) serían:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (\pm1, \pm1, \pm1)

Esto significa que las coordenadas pueden ser (1,1,1), (1,1,-1), etc. El espacio dentro del cubo incluye todos los puntos (x, y, z) donde x, y, z están entre -1 y 1.

Ecuación de un cubo en el espacio

En geometría analítica, la superficie de un cubo con centro en (x₀, y₀, z₀) y un lado de 2a unidades, está formada por todos los puntos (x, y, z) que cumplen:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \max\{ |x-x_0|,|y-y_0|,|z-z_0| \} = a.

Esto significa que la distancia más grande desde el centro a cualquiera de los ejes (x, y, z) es igual a la mitad de la longitud del lado del cubo.

El antiguo problema de duplicar un cubo

La duplicación del cubo, también conocida como el problema de Delos, fue un desafío para los matemáticos de la antigua Grecia. Querían construir, usando solo una regla y un compás, el lado de un cubo que tuviera el doble de volumen que un cubo dado. No pudieron resolverlo. En 1837, Pierre Wantzel demostró que era imposible porque la raíz cúbica de 2 no es un número que se pueda construir con regla y compás.

Colores y simetría de un cubo

Un cubo puede tener diferentes formas de ser coloreado de manera uniforme. Se nombran según los colores únicos de las caras cuadradas alrededor de cada vértice: 111, 112, 123.

El cubo tiene cuatro tipos de simetría, que se pueden ver al colorear sus caras. La simetría más alta se llama octaédrica (O_h), donde todas las caras son del mismo color. Otras simetrías, como la diédrica (D_4h), ocurren cuando las caras tienen diferentes colores.

Nombre	Hexaedro regular	Prisma cuadrado	Trapezoprisma rectangular	Cuboide rectangular	Prisma rómbico	Trapezoedro trigonal
símbolo de Schläfli	{4,3}	{4}×{ } rr{4,2}	s2{2,4}	{ }3 tr{2,2}	{ }×2{ }
símbolo de Wythoff	3 | 4 2	4 2 | 2		2 2 2 |
Simetría	Oh [4,3] (*432)	D4h [4,2] (*422)	D2d [4,2+] (2*2)	D2h [2,2] (*222)		D3d [6,2+] (2*3)
Orden de simetría	24	16	8	8		12
Imagen (colores uniformes)	(111)	(112)	(112)	(123)	(112)	(111), (112)

Relaciones geométricas del cubo

Los 11 desarrollos del cubo

Estos conocidos dados de seis caras tienen forma de cubo.

Un cubo tiene once "redes" o "desarrollos". Esto significa que hay once maneras diferentes de desdoblar un cubo hueco cortando siete de sus aristas para que quede plano.

Para pintar un cubo de manera que ninguna cara que se toque tenga el mismo color, necesitarías al menos tres colores.

El cubo es la forma básica para crear un mosaico regular en el espacio tridimensional. También es especial entre los sólidos platónicos porque sus caras tienen un número par de lados.

Un cubo se puede dividir en seis pirámides cuadradas idénticas. Si estas pirámides se unen a las caras de otro cubo, se forma un dodecaedro rómbico.

Partes de un cubo

Cubo (Matemateca Ime-Usp)

• Cara: Es cada una de las seis superficies cuadradas que forman el cubo. Cada cara tiene cuatro caras vecinas y una cara opuesta (que está al otro lado del cubo).
• Arista: Es la línea donde se unen dos caras. Un cubo tiene 12 aristas en total.
• Vértice: Es el punto donde se unen tres caras (y tres aristas). Un cubo tiene 8 vértices.
• Diagonal espacial: Es una línea recta que conecta dos vértices opuestos del cubo, pasando por su interior. Un cubo tiene cuatro diagonales espaciales, y todas se cruzan en un único punto.
• Centro: Es el punto donde se cruzan todas las diagonales espaciales del cubo. Es el punto central de la figura.

Medidas y simetría del cubo

Volumen de un cubo

Si un cubo tiene un lado de longitud a, su volumen (el espacio que ocupa) se calcula multiplicando el lado por sí mismo tres veces:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = a \cdot a \cdot a = a^3

Área de un cubo

El área total de la superficie de un cubo (la suma del área de sus seis caras) se calcula así:

El área lateral (solo las cuatro caras de los lados, sin la base ni la tapa) es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A_L = 4 \cdot A_c = 4a^2

Longitud de las diagonales

Para un cubo con lado a:

• La diagonal facial (la línea que une dos vértices opuestos en una misma cara) se calcula con el teorema de Pitágoras:

 : .

• La diagonal espacial (la línea que une dos vértices opuestos del cubo, pasando por el centro) se calcula usando la diagonal facial:

 : .

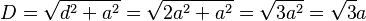Optimización del cubo

Entre todas las cajas rectangulares (ortoedros) que tienen la misma área total, el cubo es el que tiene el mayor volumen.

Simetría del cubo

Un cubo tiene mucha simetría. Tiene:

• 3 ejes de simetría de orden cuatro (líneas que lo atraviesan por el centro de las caras opuestas).
• 4 ejes de simetría de orden tres (líneas que unen vértices opuestos).
• 6 ejes de simetría de orden 2 (líneas que unen los centros de aristas opuestas).
• 9 planos de simetría (superficies que dividen el cubo en dos partes iguales y simétricas).
• Un centro de simetría (el punto central del cubo).

Todo esto le da al cubo un total de 48 formas de simetría.

Poliedro conjugado

El poliedro conjugado de un cubo con lado a es un octaedro regular con lado b, de tal manera que: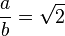

Resumen de fórmulas importantes

Para un cubo con lado a:

área de la superficie	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6 a^2\,	volumen	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^3\,
diagonal facial	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt 2a	diagonal espacial	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\textstyle \sqrt 3a}
radio de la esfera circunscrita	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\sqrt 3}{2} a	radio de la esfera tangente a los bordes	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{\sqrt 2}
radio de la esfera inscrita	Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{2}	ángulos entre caras (en radianes)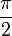

Como el volumen de un cubo se calcula elevando su lado a la tercera potencia (a x a x a), a las terceras potencias se les llama "cubo", igual que a las segundas potencias se les llama "cuadrado".

Un cubo tiene el mayor volumen entre todas las cajas rectangulares (cuboides) que tienen la misma superficie total. También tiene el mayor volumen entre cuboides con la misma suma de largo, ancho y alto.

Relación con esferas y el octaedro

Esfera inscrita en un cubo

Dentro de cualquier cubo se puede dibujar una esfera que lo toca por dentro en el centro de cada cara. El centro de esta esfera es el mismo que el del cubo, y su radio es la mitad del lado del cubo.

radio de la esfera inscrita es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r = \frac{a}{2} ; y el volumen de esta esfera es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V_e = \pi \frac {a^3}{6} , donde es el lado del cubo.

Esfera que rodea un cubo (circunscrita)

Cualquier cubo puede caber dentro de una esfera que lo toca en todos sus vértices. El centro de esta esfera es el mismo que el del cubo.

radio de la esfera circunscrita es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): R = \frac{d}{2} , y el volumen es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V_e = \pi \frac {d^3}{6} , donde 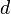es la diagonal espacial del cubo.

Octaedro dentro de un cubo

Dentro de un cubo se puede dibujar un octaedro regular. Sus vértices se ubican en el centro de las caras del cubo.

Si es el lado del cubo, el volumen del octaedro inscrito es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = \frac {a^3} {4} .

Topología del cubo

Convexidad

Un cubo es un sólido convexo. Esto significa que si pones un plano sobre cualquiera de sus caras, todo el cubo queda de un solo lado de ese plano. No tiene "curvas hacia adentro".

Interior del cubo

El "interior" del cubo son todos los puntos que están dentro de él, sin tocar ninguna de sus caras.

Frontera del cubo

La "frontera" del cubo es la superficie del cubo, es decir, todas sus seis caras. Ningún punto de la frontera está en el interior.

Exterior del cubo

El "exterior" del cubo son todos los puntos del espacio que no están ni en el interior ni en la frontera del cubo. Si juntas el interior, el exterior y la frontera, obtienes todo el espacio. Estos tres conjuntos no se superponen.

Abierto

Un conjunto de puntos se llama "abierto" si, para cualquier punto de ese conjunto, puedes dibujar una pequeña esfera alrededor de él que esté completamente dentro del conjunto. Tanto el interior como el exterior de un cubo son conjuntos abiertos.

Conexidad

El cubo es una figura "conexa", lo que significa que es una sola pieza. No se puede dividir en dos partes separadas que no se toquen.

Hipercubo: Cubos en otras dimensiones

Animación que muestra la formación de los primeros cuatro hipercubos como una extensión de cada uno hacia la siguiente dimensión.

Un hipercubo es como un cubo, pero en cualquier número de dimensiones. Son formas geométricas regulares.

Todos los hipercubos se pueden construir duplicando un hipercubo de una dimensión menor y conectando sus vértices.

Según el número de dimensiones, los hipercubos se llaman:

• Punto (0 dimensiones)
• Segmento (1 dimensión)
• Cuadrado (2 dimensiones)
• Cubo (3 dimensiones)
• Teseracto o hipercubo (4 dimensiones)
• Penteracto (5 dimensiones), y así sucesivamente.

También se les puede llamar n-cubo, donde n es el número de dimensiones.

El cubo en la cultura y la religión

En la cultura popular

Dados típicamente cúbicos: estilo occidental, estilo asiático y dados usados en casinos.

El cubo es una forma muy común en juguetes y juegos. Ejemplos famosos son los dados y el cubo de Rubik.

En la religión

Los cubos aparecen en algunas religiones. La Kaaba en La Meca, un lugar sagrado para el islam, tiene forma de cubo (su nombre en árabe significa "el cubo"). También se mencionan en el judaísmo (como las Filacteria) y en el Nuevo Testamento, donde la Nueva Jerusalén se describe como un cubo.

Ver también

• Cuadrado
• Cubo unitario
• Cubo de Rubik
• Cubo Soma
• Dado
• Ortoedro
• Policubo

Galería de imágenes

• 

  Desarrollo de un cubo

• 

  El cubo con sus esquinas, aristas y diagonales.

Véase también

En inglés: Cube Facts for Kids