Área superficial para niños
El área superficial de un objeto sólido es la medida de la superficie total que cubre el exterior de ese objeto. Imagina que quieres envolver un regalo: la cantidad de papel que necesitas para cubrirlo por completo sería su área superficial.
Para objetos con lados planos, como una caja, calcular el área superficial es sencillo: solo sumas el área de cada una de sus caras. Pero para objetos con superficies curvas, como una pelota, la definición matemática es un poco más compleja. Los matemáticos Henri Léon Lebesgue y Hermann Minkowski trabajaron en el siglo XX para encontrar una forma general de definir el área de superficies, incluso las más irregulares.
Contenido
¿Qué es el Área Superficial?
El área superficial es como la "piel" de un objeto tridimensional. Es una medida de cuánto espacio ocupa la parte exterior de algo.
Propiedades Clave del Área Superficial
Para que una medida sea considerada área superficial, debe cumplir algunas reglas importantes:
- Aditividad: Si divides un objeto en varias partes, el área superficial total del objeto es la suma de las áreas superficiales de todas sus partes. Por ejemplo, si cortas una manzana en pedazos, la suma de las superficies de esos pedazos es igual a la superficie original de la manzana (sin contar las superficies de corte).
- Forma y Posición: El área superficial de un objeto solo depende de su forma y tamaño. No importa si lo giras, lo mueves o lo colocas en un lugar diferente; su área superficial seguirá siendo la misma.
- Coincidencia con Áreas Planas: Para figuras planas, como un cuadrado o un triángulo, el área superficial es igual a su área normal, la que ya conoces.
¿Por qué es difícil calcular el área de superficies curvas?
A diferencia de las figuras planas o los objetos con caras rectas, las superficies curvas son más complicadas. No se pueden medir fácilmente con una regla. Los matemáticos usan herramientas avanzadas, como el cálculo, para encontrar el área de estas superficies.
Un ejemplo interesante es la "linterna de Schwarz". Hermann Amandus Schwarz demostró que si intentas calcular el área de un cilindro aproximándolo con muchas figuras planas pequeñas, el resultado puede variar mucho dependiendo de cómo hagas esas aproximaciones. Esto muestra lo delicado que es definir el área para superficies curvas.
Fórmulas Comunes para el Área Superficial
Aquí tienes algunas fórmulas para calcular el área superficial de objetos comunes:
| Forma | Ecuación | Variables |
|---|---|---|
| Cubo | 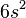 |
s = largo del lado |
| Ortoedro | 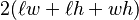 |
ℓ = largo, w = ancho, h = altura |
| Prismas |  |
B = el área de una base, P = el perímetro de una base, h = altura |
| Esfera | 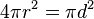 |
r = radio de la esfera, d = diámetro |
| Cilindro cerrado | 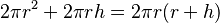 |
r = radio de la base circular, h = altura del cilindro |
| Área superficial total de un cono | 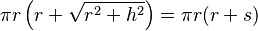 |
s = altura inclinada del cono, r = radio de la base circular, h = altura del cono |
| Pirámide | 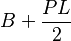 |
B = área de la base, P = perímetro de la base, L = altura inclinada |
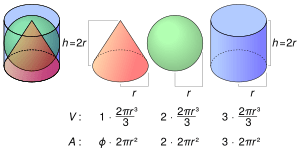
La Relación entre Esferas y Cilindros
Un dato curioso, descubierto por el antiguo matemático Arquímedes, es la relación entre el área superficial de una esfera y un cilindro. Si tienes una esfera y un cilindro que tienen el mismo radio y la altura del cilindro es igual al diámetro de la esfera (es decir, el cilindro "envuelve" perfectamente a la esfera), sus áreas superficiales guardan una proporción especial:
- El área de la esfera es
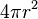 .
. - El área del cilindro es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \pi r (h + r) . Si la altura h es igual a 2r (el diámetro de la esfera), entonces el área del cilindro es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \pi r (2r + r) = 2 \pi r (3r) = 6 \pi r^2 .
Esto significa que la relación entre el área de la esfera y el área del cilindro es de 4 a 6, que se simplifica a 2 : 3. ¡Es como si la esfera ocupara dos tercios de la superficie del cilindro que la contiene!
Importancia del Área Superficial en la Ciencia
En Química
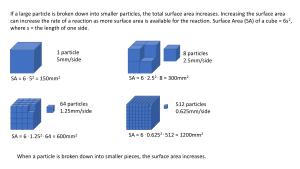
El área superficial es muy importante en las reacciones químicas. Cuanto mayor sea el área superficial de una sustancia, más rápido puede reaccionar. Por ejemplo, el hierro en polvo fino se quema muy rápido, mientras que un bloque grande de hierro es muy estable. Esto se debe a que el polvo tiene mucha más superficie expuesta al aire para reaccionar.
En Biología
En los seres vivos, el área superficial es crucial para muchas funciones:
- Regulación de la temperatura: Los animales con orejas grandes, como los elefantes, usan su gran área superficial para liberar calor y mantenerse frescos. Cuando tenemos frío, nos encogemos para reducir nuestra área superficial y conservar el calor.
- Digestión: Nuestros dientes trituran la comida para aumentar su área superficial, lo que ayuda a que las enzimas digestivas actúen más rápido. Dentro de nuestro intestino, hay unas pequeñas estructuras llamadas microvellosidades que aumentan enormemente el área para absorber nutrientes.
- Tamaño de las células: La relación entre el área superficial y el volumen de una célula es muy importante. Las células necesitan absorber nutrientes y eliminar desechos a través de su superficie. Si una célula crece demasiado, su volumen aumenta mucho más rápido que su área superficial. Esto significa que no tendría suficiente "puerta de entrada" (superficie) para que pasen los nutrientes y desechos, lo que limitaría su tamaño. Por eso, las células suelen ser muy pequeñas.
Véase también
 En inglés: Surface area Facts for Kids
En inglés: Surface area Facts for Kids
- Longitud del perímetro
- Teoría BET, una técnica para medir el área superficial de materiales.