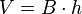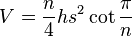Prisma (geometría) para niños

Datos para niños Prisma
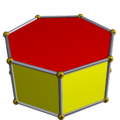
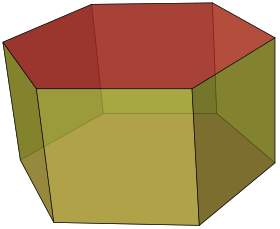Imagen del sólido
Caras	n + 2
Polígonos que forman las caras	2 n-ágonos n cuadrados
Aristas	3n
Vértices	2n
Configuración de vértices	4.4.n
Grupo de simetría	Dnh
Poliedro dual	Bipirámide n-gonal
Símbolo de Schläfli	{n}×{ } t{2,n}
Símbolo de Coxeter-Dynkin
Conway	Pn
Propiedades
Prismatoide
Desarrollo

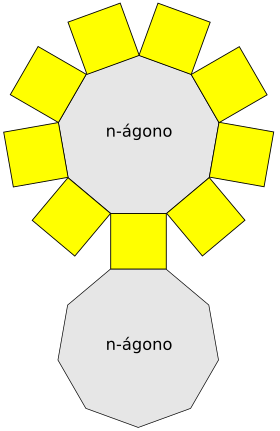Un prisma es una figura geométrica tridimensional. Es un tipo de poliedro, lo que significa que tiene caras planas. Un prisma se caracteriza por tener dos caras que son exactamente iguales y están colocadas de forma paralela. Estas caras se llaman bases. Las demás caras del prisma son paralelogramos.

Los prismas reciben su nombre según la forma de sus bases. Por ejemplo, si las bases son pentágonos (figuras de cinco lados), se llama prisma pentagonal. La palabra "prisma" viene del griego y significa "algo aserrado".

¿Qué es un Prisma?

Un prisma es un poliedro que cumple dos condiciones importantes:

• Tiene exactamente dos caras que son idénticas y están en planos paralelos. Estas son sus bases.
• Todas las demás caras son paralelogramos.

Partes de un Prisma

Cada prisma tiene elementos clave que lo forman:

• Bases: Son las dos caras idénticas y paralelas. Una es la base inferior y la otra la superior.
• Caras laterales: Son las caras que conectan las dos bases. Siempre son paralelogramos.
• Aristas: Son los segmentos donde se unen dos caras.
• Vértices: Son los puntos donde se encuentran tres o más aristas.
• Altura: Es la distancia perpendicular entre las dos bases.
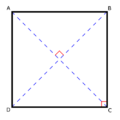
• Diagonales: Son líneas que unen dos vértices que no están conectados por una arista. Pueden estar en una cara o conectar vértices de diferentes caras.

Tipos de Prismas

Los prismas se clasifican según la forma de sus bases y cómo se unen sus caras laterales.

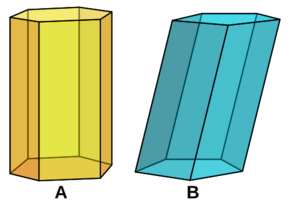
Prisma Recto vs. Prisma Oblicuo

Prisma recto (A) y prisma oblicuo (B)

• Un prisma recto es aquel donde las caras laterales son rectángulos. Esto significa que las aristas que conectan las bases son perpendiculares a las bases.
• Un prisma oblicuo es un prisma donde las caras laterales no son rectángulos, sino paralelogramos inclinados. Las aristas que unen las bases no son perpendiculares a ellas.

Prisma Regular

Un prisma regular es un prisma recto cuyas bases son polígonos regulares. Un polígono regular tiene todos sus lados y ángulos iguales.

Prisma Uniforme

Un prisma uniforme es un tipo especial de prisma recto. Sus bases son polígonos regulares y todas sus aristas (tanto las de las bases como las que conectan las bases) tienen la misma longitud. Esto significa que todas sus caras laterales son cuadrados.

Calcular la Superficie de un Prisma

Para encontrar el área total de la superficie de un prisma recto, necesitas sumar el área de sus dos bases y el área de todas sus caras laterales.

La fórmula general es:

Área total = 2 × (Área de la base) + (Perímetro de la base × Altura)

Si la base es un polígono regular de n lados, con longitud de lado s y la altura del prisma es h, la fórmula se ve así:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{n}{2} s^2 \cot \left( \frac{\pi}{n} \right) + n s h .

Calcular el Volumen de un Prisma

El volumen de un prisma es la cantidad de espacio que ocupa. Se calcula multiplicando el área de una de sus bases por su altura.

La fórmula es:

Donde B es el área de la base y h es la altura del prisma.

Si la base es un polígono regular de n lados con una longitud de lado s, la fórmula para el volumen es:

Casos Especiales de Prismas

• Un cuboide es un prisma recto con bases rectangulares. También se le conoce como "caja rectangular".
• Un cubo es un caso especial de cuboide donde todas sus caras son cuadrados. Es un prisma recto con bases cuadradas y todas sus aristas de la misma longitud.
• Un paralelepípedo es un prisma oblicuo cuyas bases son paralelogramos. Todas sus seis caras son paralelogramos.

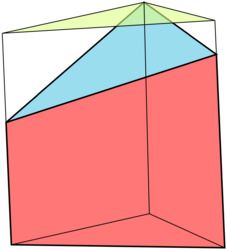
Prisma Truncado

Ejemplo de prisma triangular truncado. Su cara superior está cortada en un ángulo inclinado.

Un prisma truncado es una parte de un prisma que se obtiene al cortar el prisma con un plano que no es paralelo a sus bases y que atraviesa todas sus aristas laterales. Esto hace que las dos bases resultantes no sean iguales y que las caras laterales no sean paralelogramos.

Galería de imágenes

• 

  Prisma triangular

• 

  Prisma cuadrangular (cubo)

• 

  Prisma pentagonal

• 

  Prisma hexagonal

• 

  Prisma heptagonal

• 

  Prisma octagonal

• 

  Poliedro de Schönhardt (prisma triangular torcido)

• 

  Prisma cuadrado torcido

• 

  Antiprisma cuadrado

• 

  Prisma dodecagonal torcido

• 

  Tronco pentagonal

• 

  Prisma cruzado cuadrado

• 

  Prisma cruzado hexagonal

• 

  Prisma cruzado hexagonal desigual

• 

  Prisma estrellado pentagrámico

• 

  Prisma estrellado heptagrámico (7/2)

• 

  Prisma estrellado heptagrámico (7/3)

• 

  Prisma estrellado octagrámico (8/3)

• 

  Prisma cruzado cuadrado (doble cruce)

• 

  Prisma cruzado hexagonal (doble cruce)

• 

  Prisma cruzado hexagonal desigual (doble cruce)

• 

  Prisma triangular cruzado

• 

  Cubo cruzado

• 

  Prisma pentagonal cruzado

• 

  Prisma pentagrámico cruzado

• 

  Prisma hexagonal cruzado

• 

  Prisma toroidal cuadrado

• 

  Prisma toroidal hexagonal

• 

  Segmento de recta (prisma 0-politópico)

• 

  Cuadrado (prisma 1-politópico)

• 

  Prisma pentagonal (prisma poligonal)

• 

  Prisma dodecaédrico (prisma poliédrico)

• 

  Duoprisma {23}×{29}

• 

  Prisma triangular

• 

  Prisma cuadrangular

• 

  Prisma pentagonal

• 

  Prisma hexagonal

• 

  Prisma heptagonal

• 

  Prisma octagonal

• 

  Prisma eneagonal

• 

  Prisma decagonal

• 

  Prisma endecagonal

• 

  Prisma dodecagonal

Ver también

• Antiprisma
• Cilindro

Véase también

En inglés: Prism (geometry) Facts for Kids