Triángulo isósceles para niños
Datos para niños Triángulo isósceles |
||
|---|---|---|
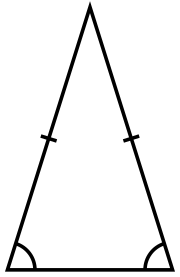 Imagen del polígono
|
||
| Características | ||
| Lados | 3 | |
| Vértices | 3 | |
| Grupo de simetría | Dih2, [ ], (*), orden 2 | |
| Símbolo de Schläfli | ( ) ∨ { } | |
| Propiedades | ||
| Polígono convexo, cíclico y autodual |
||
En geometría, un triángulo isósceles es un triángulo que tiene dos lados con la misma longitud. Al ángulo que se forma entre estos dos lados iguales se le llama ángulo del vértice. El lado opuesto a este ángulo se conoce como lado base.
Contenido
- ¿Qué significa "isósceles" en geometría?
- ¿Cómo calcular el área de un triángulo isósceles?
- Propiedades y simetría de los triángulos isósceles
- Teorema del triángulo isósceles
- ¿Cómo se pueden dividir los triángulos en triángulos isósceles?
- Curiosidades sobre los triángulos isósceles
- La falacia del triángulo isósceles
- Véase también
¿Qué significa "isósceles" en geometría?
La palabra "isósceles" viene de dos palabras griegas: "isos" que significa "igual" y "skelos" que significa "pierna". Esta misma palabra se usa para otras figuras, como el trapecio isósceles, que también tiene dos lados iguales. Un triángulo que no es isósceles, es decir, que tiene sus tres lados de diferentes longitudes, se llama escaleno.
Partes de un triángulo isósceles
En un triángulo isósceles que tiene solo dos lados iguales, a estos lados se les llama patas. El tercer lado, el que es diferente, se llama base. El ángulo que está entre las patas se conoce como ángulo del vértice. Los otros dos ángulos, que están junto a la base, se llaman ángulos de la base. El punto más alto, opuesto a la base, se llama ápice.
El matemático griego Euclides definió el triángulo isósceles como uno con exactamente dos lados iguales. Sin embargo, hoy en día, muchos lo definen como un triángulo que tiene al menos dos lados iguales. Esto significa que los triángulos equiláteros, que tienen sus tres lados iguales, también pueden considerarse un tipo especial de triángulo isósceles. En un triángulo equilátero, como todos los lados son iguales, cualquiera de ellos puede ser la base si es necesario.
Tipos de triángulos isósceles según sus ángulos
Un triángulo isósceles puede ser obtuso, recto o agudo. Esto depende del ángulo del vértice. En la Geometría euclidiana, los ángulos de la base nunca pueden ser obtusos (más de 90°) ni rectos (igual a 90°). Esto se debe a que la suma de los tres ángulos de cualquier triángulo siempre es 180°. Si los ángulos de la base fueran rectos u obtusos, la suma de solo dos de ellos ya sería 180° o más, lo cual no es posible.
Por lo tanto, un triángulo isósceles es:
- Obtuso si su ángulo del vértice es obtuso.
- Recto si su ángulo del vértice es recto.
- Agudo si su ángulo del vértice es agudo.
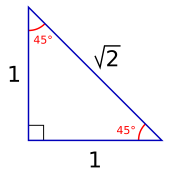
Además del triángulo isósceles rectángulo, existen otros triángulos isósceles especiales. Algunos ejemplos son el triángulo de Calabi, el triángulo áureo y el gnomon áureo.
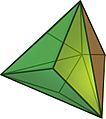
También, algunos sólidos de Catalan (que son figuras 3D con caras planas) tienen caras que son triángulos isósceles. Estos incluyen el triaquistetraedro, el triaquisoctaedro, el tetraquishexaedro, el pentaquisdodecaedro y el triaquisicosaedro.
¿Cómo calcular el área de un triángulo isósceles?
Para calcular el área de un triángulo isósceles, puedes usar una fórmula basada en la longitud de sus lados. Si los lados iguales miden a y la base mide b, la altura h (la línea que va desde el vértice hasta la base, formando un ángulo recto) se puede encontrar con el teorema de Pitágoras.
La fórmula general para el área de cualquier triángulo es: Área = (base × altura) / 2
Para un triángulo isósceles, si la base es b y la altura es h, el área T se calcula como: T = (b × h) / 2
Si conoces el ángulo del vértice (llamémoslo θ) y la longitud de las patas (a), también puedes calcular el área con la fórmula: T = (1/2) * a² * seno(θ)
Propiedades y simetría de los triángulos isósceles
Eje de simetría
Un triángulo que tiene exactamente dos lados iguales posee una línea de simetría. Esta línea pasa por el vértice del ángulo (donde se unen los dos lados iguales) y también por el punto medio de la base. Esto significa que si doblaras el triángulo por esa línea, las dos mitades coincidirían perfectamente.
Esta línea de simetría es muy especial porque coincide con varias líneas importantes del triángulo:
- La bisectriz del ángulo del vértice (divide el ángulo en dos partes iguales).
- La mediana que va desde el vértice hasta el punto medio de la base.
- La altura que baja desde el vértice hasta la base.
- La mediatriz de la base (una línea perpendicular que pasa por el punto medio de la base).
La línea de Euler
La recta de Euler es una línea especial que conecta tres puntos importantes en cualquier triángulo: el ortocentro (donde se cruzan las alturas), el centroide (donde se cruzan las medianas) y el circuncentro (el centro del círculo que pasa por los tres vértices).
En un triángulo isósceles con solo dos lados iguales, la línea de Euler es la misma que su eje de simetría. Esto ocurre porque el eje de simetría ya contiene a la altura, la mediana y la mediatriz que salen del vértice principal. Por lo tanto, los puntos donde se cruzan estas líneas (ortocentro, centroide y circuncentro) deben estar sobre el eje de simetría.
Si el ángulo del vértice es agudo, estos tres puntos (ortocentro, centroide y circuncentro) están dentro del triángulo. Si el ángulo del vértice es obtuso, el centroide sigue dentro, pero el circuncentro y el ortocentro caen fuera del triángulo.
El incentro (el centro del círculo que se puede dibujar dentro del triángulo tocando sus tres lados) también se encuentra en la línea de Euler de un triángulo isósceles.
Teorema del triángulo isósceles
Un teorema muy conocido, que aparece en el libro de Euclides, dice que los ángulos de la base de un triángulo isósceles son siempre iguales. Este resultado se conoce a veces como el "pons asinorum", que significa "el puente de los asnos". Algunos creen que este nombre se debe a la forma del dibujo que Euclides usó para demostrarlo. Otros piensan que se llama así porque era el primer problema difícil en los estudios de Euclides, y servía para distinguir a quienes podían entender la geometría de quienes no.
¿Cómo se pueden dividir los triángulos en triángulos isósceles?
Cualquier triángulo se puede dividir en n triángulos isósceles, siempre que n sea un número igual o mayor que 4.
En un triángulo rectángulo, si dibujas una línea desde el punto medio de la hipotenusa (el lado más largo) hasta el vértice del ángulo recto, esta línea divide el triángulo en dos triángulos isósceles. Esto sucede porque el punto medio de la hipotenusa es el centro del círculo que pasa por los tres vértices del triángulo rectángulo. Así, los dos triángulos pequeños tienen dos lados que son radios de ese círculo, y por lo tanto, son iguales.
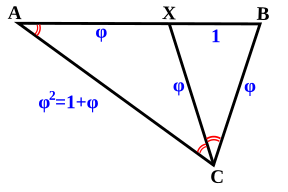
El triángulo áureo es un triángulo isósceles especial. Sus ángulos miden 72°, 72° y 36°. Se puede dividir en otro triángulo áureo más pequeño y en un gnomon áureo, que también es isósceles.
Curiosidades sobre los triángulos isósceles
La diagonal de un rombo (una figura de cuatro lados iguales) lo divide en dos triángulos isósceles que son exactamente iguales.
La falacia del triángulo isósceles
Existe una famosa demostración falsa que intenta "probar" que "todos los triángulos son isósceles". Esta idea se ha atribuido a Lewis Carroll, el autor de "Alicia en el País de las Maravillas". La trampa en esta "prueba" está en que no se considera bien si ciertas líneas o puntos están dentro o fuera de la figura, lo que lleva a un error en el razonamiento.
Véase también
 En inglés: Isosceles triangle Facts for Kids
En inglés: Isosceles triangle Facts for Kids