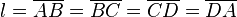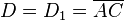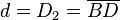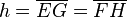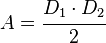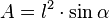Rombo para niños
Datos para niños Rombo |
||
|---|---|---|
Cuatro lados iguales y paralelos dos a dos y sus cuatro ángulos oblicuos
|
||
| Características | ||
| Tipo | Cuadrilátero, paralelogramo | |
| Lados | 4 | |
| Vértices | 4 | |
| Grupo de simetría | Diedral (D2), [2], (*22), orden 4 | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Rectángulo | |
| Propiedades | ||
| Convexo, cíclico Ángulos opuestos y lados cogruentes. |
||
El rombo es una figura geométrica plana. Es un paralelogramo, lo que significa que tiene dos pares de lados paralelos. La característica principal del rombo es que sus cuatro lados tienen la misma longitud. Por eso, a veces se le llama cuadrilátero equilátero.
También se le conoce como diamante por su parecido con la forma de los diamantes en los naipes. A veces, el término "diamante" se usa para un rombo con un ángulo de 60 grados.
Contenido
¿Qué es un Rombo?
Un rombo es un tipo especial de paralelogramo. Para que una figura sea un rombo, debe cumplir que sus cuatro lados midan lo mismo.
Características Clave del Rombo
Un cuadrilátero (una figura de cuatro lados) es un rombo si cumple alguna de estas condiciones:
- Es un paralelogramo donde una de sus diagonales divide un ángulo interior en dos partes iguales.
- Es un paralelogramo donde al menos dos lados que están juntos tienen la misma longitud.
- Es un paralelogramo donde sus diagonales se cruzan formando un ángulo recto (90 grados).
- Es un cuadrilátero con sus cuatro lados de igual longitud.
- Es un cuadrilátero donde las diagonales se cruzan en ángulo recto y se dividen por la mitad.
- Es un cuadrilátero donde cada diagonal divide por la mitad los dos ángulos opuestos.
Si un rombo tiene un ángulo recto (90 grados), entonces se convierte en un cuadrado.
Historia del Rombo
La palabra rombo viene de la forma que tiene un huso (una herramienta para hilar) lleno de hilo. El famoso matemático Euclides mencionó el rombo en sus libros de geometría, aunque no profundizó mucho en sus propiedades. Otros matemáticos como Herón de Alejandría y Papo de Alejandría también hablaron de esta figura.
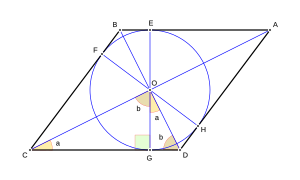
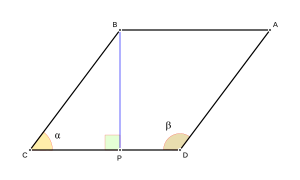
Elementos y Medidas del Rombo
En un rombo, podemos identificar varias partes importantes:
- El lado (l): Todos los lados son iguales.
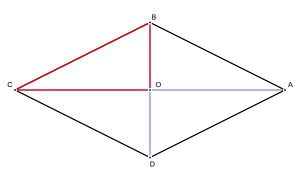
- Las diagonales (D y d): Son las líneas que conectan vértices opuestos. Hay una diagonal mayor (D) y una diagonal menor (d).
- La altura (h): Es la distancia perpendicular entre dos lados paralelos.
Propiedades del Rombo
Los rombos tienen propiedades muy interesantes:
- Las diagonales de un rombo siempre se cruzan formando un ángulo recto (90 grados).
- Las diagonales también dividen los ángulos del rombo en dos partes iguales.
- Los ángulos opuestos de un rombo son iguales.
- El punto donde se cruzan las diagonales es el centro del rombo. Este punto divide cada diagonal en dos partes iguales.
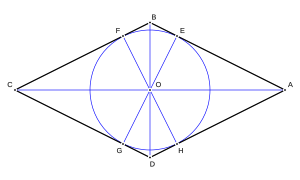
- Si unes los puntos medios de los lados de un rombo, la figura que se forma es un rectángulo.
- El rombo tiene simetría central, lo que significa que si lo giras 180 grados alrededor de su centro, se verá igual.
¿Cómo Calcular el Área de un Rombo?
El área es la medida de la superficie que cubre una figura. Para el rombo, hay varias formas de calcularla:
Usando las Diagonales
La forma más común de calcular el área de un rombo es multiplicando la longitud de sus dos diagonales y luego dividiendo el resultado entre dos.
Donde D1 es la diagonal mayor y D2 es la diagonal menor.
Usando un Lado y la Altura
También puedes calcular el área multiplicando la longitud de uno de sus lados por su altura.
-
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = l \cdot h
Donde l es la longitud de un lado y h es la altura del rombo.
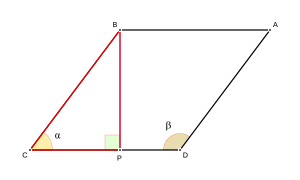
Usando un Lado y un Ángulo
Otra forma es multiplicar el cuadrado de la longitud de un lado por el seno de uno de sus ángulos.
Donde l es el lado y α es el ángulo entre dos lados.
Simetría del Rombo
- Las diagonales del rombo son como espejos: si doblas el rombo por una diagonal, las dos mitades coinciden. Esto se llama simetría axial.
- El punto donde se cruzan las diagonales es el centro de simetría central. Si giras el rombo 180 grados alrededor de este punto, la figura se ve exactamente igual.
Otros Datos Curiosos del Rombo
- Los rombos pueden usarse para cubrir una superficie sin dejar huecos, a esto se le llama teselado. Hay varias formas de hacer teselados con rombos.
| Como teselados cuadrados | Como teselado rómbico | |
|---|---|---|
- En tres dimensiones, existen figuras como la bipirámide y el bicono que son como rombos extendidos.
- Muchos poliedros (figuras 3D con caras planas) tienen caras en forma de rombo. Algunos ejemplos son el rombododecaedro y el triacontaedro rómbico.
| Poliedros con rombos idénticos | Poliedros con diferentes tipos de rombos | |||
|---|---|---|---|---|
| Rombos idénticos | Rombos áureos idénticos | Dos tipos de rombos | Tres tipos de rombos | |
| Rombododecaedro | Triacontaedro rómbico | Icosaedro rómbico | Eneacontaedro rómbico | Romboedro |
Rombos en Poliedros
Un romboedro es una figura 3D cuyas seis caras son rombos. Es similar a un cubo, pero con caras inclinadas.
El rombododecaedro es un poliedro con 12 caras que son rombos iguales.
El triacontaedro rómbico tiene 30 caras, todas ellas rombos especiales llamados "rombos áureos".
El Rombo en la Vida Cotidiana

Logo de Renault (2009)
|
El rombo es una forma que vemos a menudo a nuestro alrededor:
- Los logotipos de marcas de coches como Mitsubishi y Renault usan la forma del rombo.
- En la Televisión Española se usaban símbolos de rombos para indicar la clasificación de los programas por edades.
- Las pastillas Juanola tienen una forma de rombo muy característica.
- En los naipes, el palo de "diamantes" tiene figuras en forma de rombo.
- Una cometa es un ejemplo sencillo de un rombo en la vida real.
- A veces, en puertas de madera, se tallan rombos como decoración.
Véase también
 En inglés: Rhombus Facts for Kids
En inglés: Rhombus Facts for Kids
- Paralelogramo
- Cuadrado
- Rectángulo
- Romboide
- Deltoide
- Rombo áureo
- Losange (heráldica)
- Macla